- 利用函數計算n! 一個簡單的函數副程式用法def。在下面這個程式當中我們把n!的連乘計算,寫成一個函數程式,再來呼叫使用它。並且我們在函數程式中也定義的0!=1。
- \(\sin(x)\)函數的級數展開 正弦函數(\(\sin(x)\))的級數定義:
- 導入數學函數: 在這個程式當中我們將經常使用的數學函數呼叫進來做示範。
直接在主程式中連乘:
S=1
for i in range(1,6):
S*=i
print(i,S)
|
1 1 2 2 3 6 4 24 5 120 |
定義階乘函數:
def factorial(n):
S=1
for i in range(1,n+1):
S*=i
return S
S=factorial(6)
print('6!=',S)
|
6!= 720 |
|
重複呼叫階乘函數:0!=1 在這個程式中我們呼叫了數學函數庫:import math
def factorial(n):
if(n==0): return 1
S=1
for i in range(1,n+1):
S*=i
return S
for j in range(8):
S=factorial(j)
print(j,'!=',S)
|
0 != 1 1 != 1 2 != 2 3 != 6 4 != 24 5 != 120 6 != 720 7 != 5040 |
\( \sin(x)=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\frac{x^9}{9!}+\cdots=\sum_{n=0}^{\infty}\frac{(-1)^n x^{2n+1}}{(2n+1)!} \)
利用函數程式facto計算n!再按公式做級數求和,最後與數學涵數庫的\(\sin(x)\)比較。
def factorial(n):
if(n==0): return 1
S=1
for i in range(1,n+1):
S*=i
return S
import math
N=10
x=math.pi/4
S=0
for n in range(0,N):
an = (-1.)**n / factorial(2*n+1) * x**(2*n+1)
S += an
print('%4d %8.4f %8.4f ' %(n,an,S))
print('%4d %8.4f %8.4f %8.4f ' %(N,x,S,math.sin(x)))
|
0 0.7854 0.7854 1 -0.0807 0.7047 2 0.0025 0.7071 3 -0.0000 0.7071 4 0.0000 0.7071 5 -0.0000 0.7071 6 0.0000 0.7071 7 -0.0000 0.7071 8 0.0000 0.7071 9 -0.0000 0.7071 10 0.7854 0.7071 0.7071 |
math
x=pi/3.
deg=math.degrees(x) #將弧度轉為角度
print('x=',x,' degree of x=',deg)
print('sin(x)=',math.sin(x)) #三角函數
print('cos(x)=',math.cos(x))
print('tan(x)=',math.tan(x))
deg2=45.
rad2=math.radians(deg2) #將角度轉為弧度
print('deg2=',deg2,' rad2=',rad2)
y=math.atan(rad2) #反三角函數
print('atan(rad2)=',y)
x=1.
print('x=',x,' 自然指數exp(x)=',math.exp(x))
print('exp(2)=',math.exp(2.))
z=10.
print('z=',z,' 自然對數log(z)=',math.log(10.))
print('常用對數log10(z)=',math.log10(10.))
print('log10(12345.)=',math.log10(12345.))
print('開平方根math.sqrt(100.)=',math.sqrt(100.))
print('math.sqrt(2.)=',math.sqrt(2.))
|
pi= 3.141592653589793 x= 1.0471975511965976 degree of x= 59.99999999999999 sin(x)= 0.8660254037844386 cos(x)= 0.5000000000000001 tan(x)= 1.7320508075688767 deg2= 45.0 rad2= 0.7853981633974483 atan(rad2)= 0.6657737500283538 x= 1.0 自然指數exp(x)= 2.718281828459045 exp(2)= 7.38905609893065 z= 10.0 自然對數log(z)= 2.302585092994046 常用對數log10(z)= 1.0 log10(12345.)= 4.091491094267951 開平方根math.sqrt(100.)= 10.0 math.sqrt(2.)= 1.4142135623730951 絕對值:x,math.fabs(x)= -10.0 10.0 |
numpy
import numpy as np
pi=np.pi
x=pi/3
print(np.sin(x))
print(np.cos(x))
a=np.linspace(0,pi,11)
print('a=',a[0:3],)
b=np.arange(0,pi,0.1)
Lb=len(b)
print('b=',b[Lb-4:Lb])
|
0.8660254037844386 0.5000000000000001 a= [0. 0.31415927 0.62831853] b= [2.8 2.9 3. 3.1] |
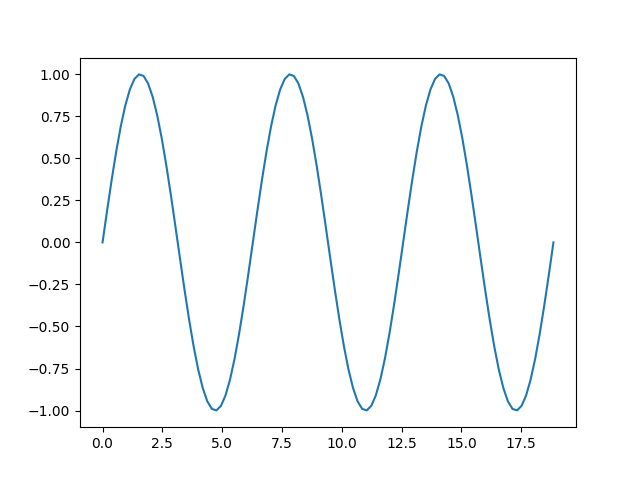
matplotlib
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0,2,11)
y = x**2
plt.figure()
plt.xlabel('x')
plt.ylabel('y')
plt.plot(x,y)
|
|
random
import random
random.seed(1234)
for i in range(10):
r=random.random()
print('%8d %8.3f %3d' %(i,r,int(r*10)))
|
0 0.966 9
1 0.441 4
2 0.007 0
3 0.911 9
4 0.939 9
5 0.582 5
6 0.672 6
7 0.084 0
8 0.766 7
9 0.237 2
|