計算物理


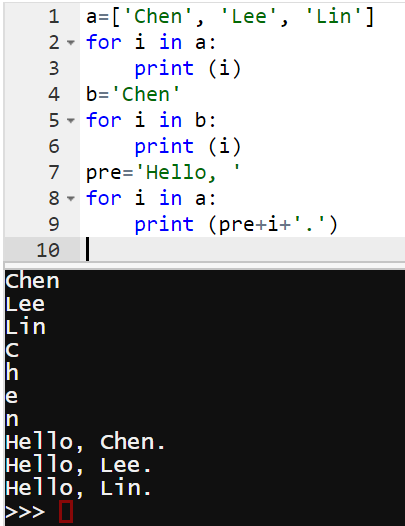
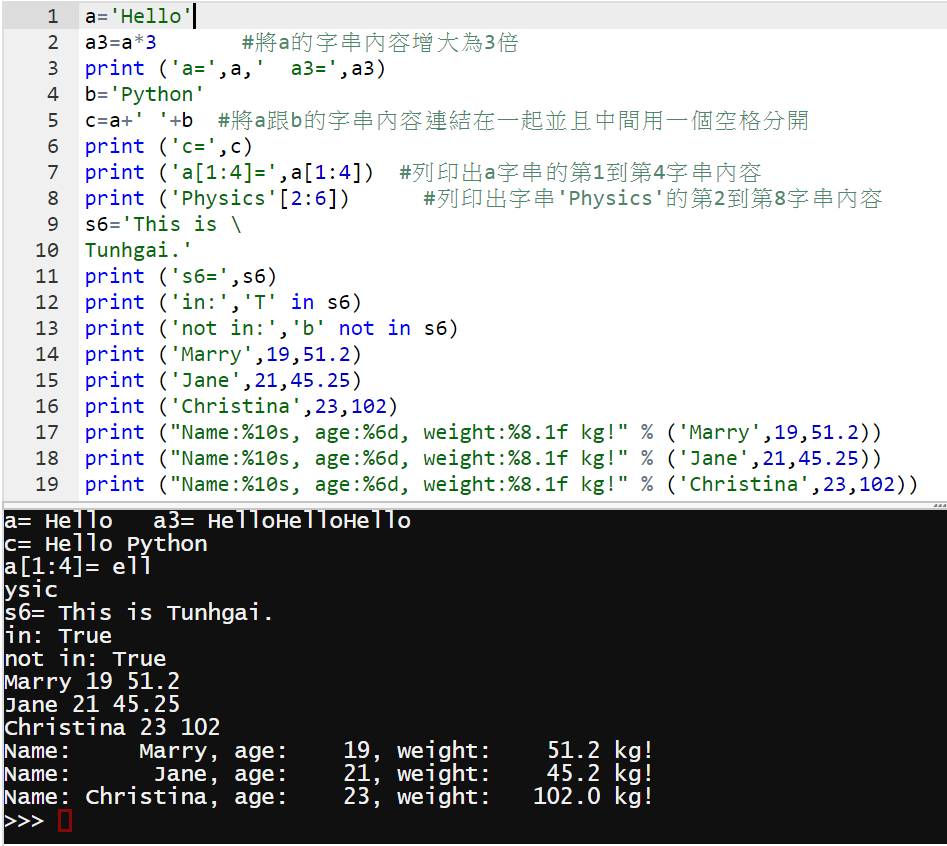
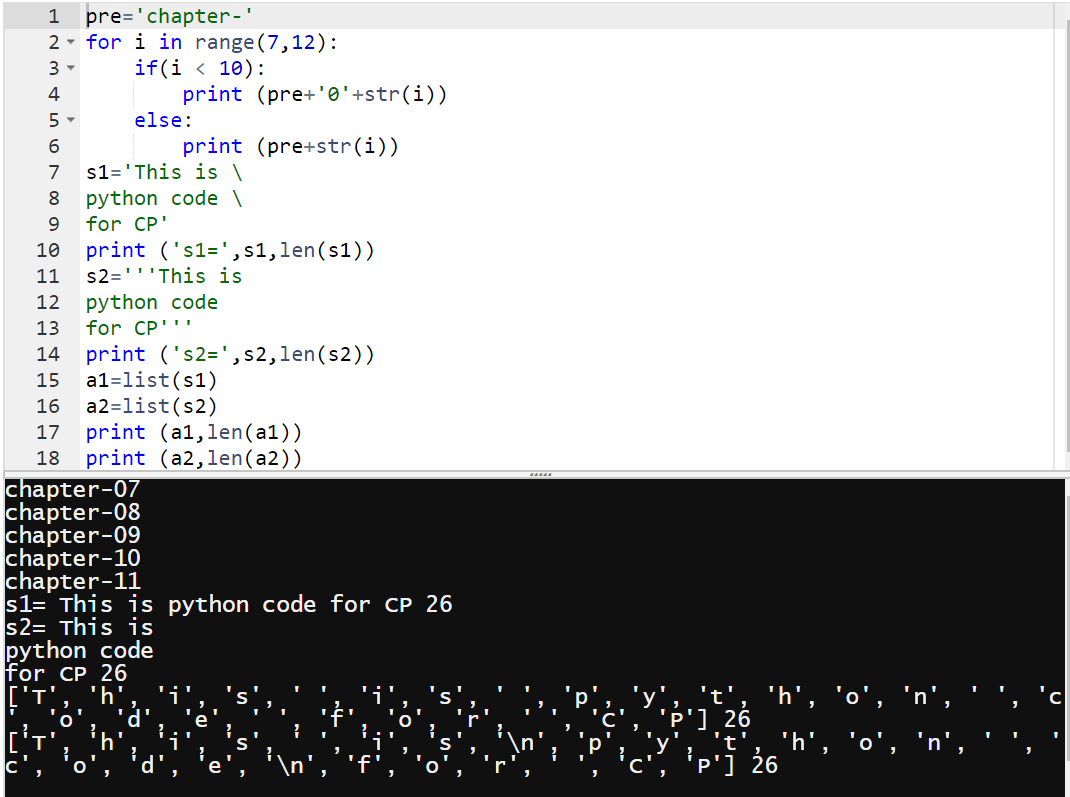
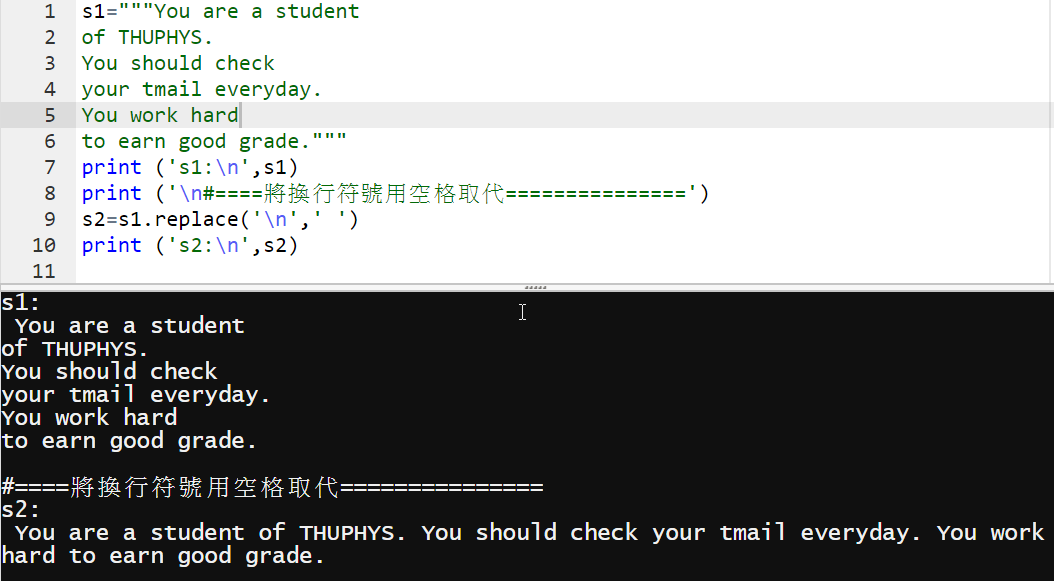
s1="""
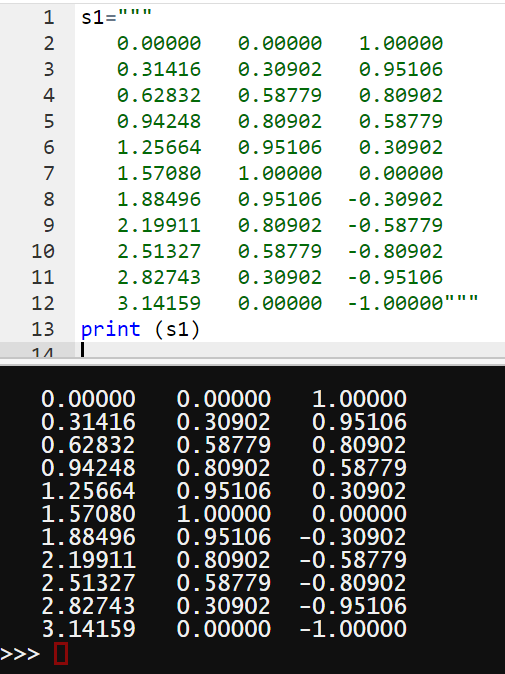
   0.00000   0.00000   1.00000
   0.31416   0.30902   0.95106
   0.62832   0.58779   0.80902
   0.94248   0.80902   0.58779
   1.25664   0.95106   0.30902
   1.57080   1.00000   0.00000
   1.88496   0.95106  -0.30902
   2.19911   0.80902  -0.58779
   2.51327   0.58779  -0.80902
   2.82743   0.30902  -0.95106
   3.14159   0.00000  -1.00000"""
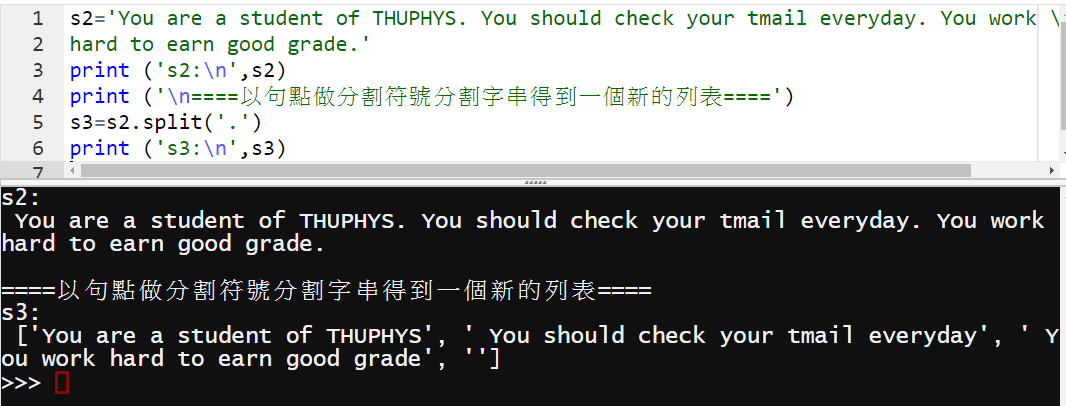
s2=s1.replace('\n',' ')
s3=s2.split(' ')
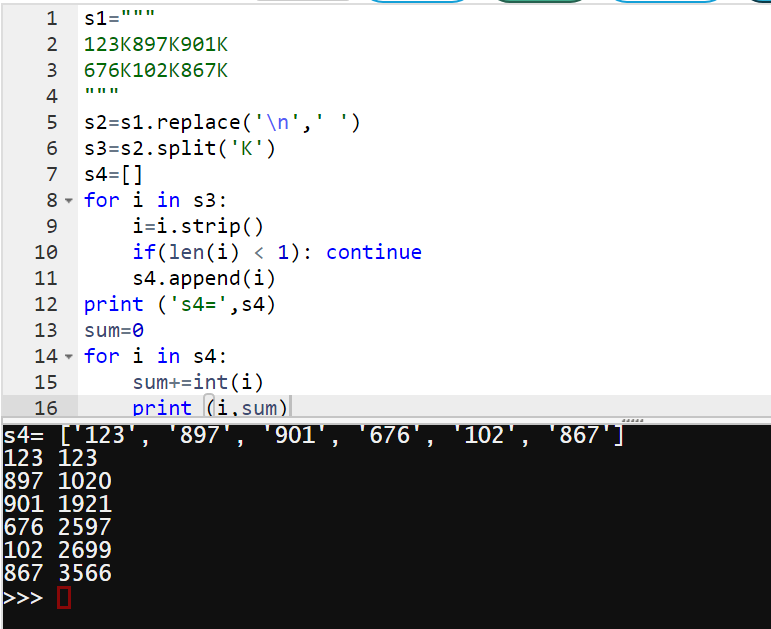
s4=[]
for i in s3:
    if(len(i) < 1): continue
    s4.append(i)
print ('s4=',s4)
NL=len(s4)
Nx=int(NL/3)
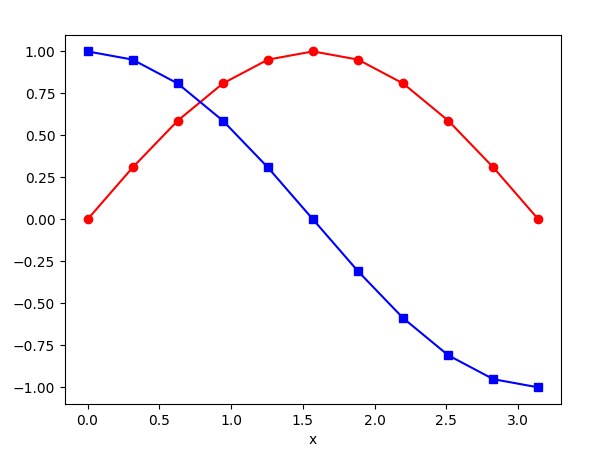
x=[]; sinx=[]; cosx=[]
for i in range(0,NL,3):
    x.append(float(s4[i]))
    sinx.append(float(s4[i+1]))
    cosx.append(float(s4[i+2]))
sum1=0.; sum2=0.
for i in range(Nx):
    sum1+=sinx[i]
    sum2+=cosx[i]
    print ('%10.5f'*5 %(x[i],sinx[i],cosx[i],sum1,sum2))
print ('sum1=',sum1,'  sum2=',sum2)


s4= ['0.00000', '0.00000', '1.00000', '0.31416', '0.
30902', '0.95106', '0.62832', '0.58779', '0.80902', 
'0.94248', '0.80902', '0.58779', '1.25664', '0.95106
', '0.30902', '1.57080', '1.00000', '0.00000', '1.88
496', '0.95106', '-0.30902', '2.19911', '0.80902', '
-0.58779', '2.51327', '0.58779', '-0.80902', '2.8274
3', '0.30902', '-0.95106', '3.14159', '0.00000', '-1
.00000']
   0.00000   0.00000   1.00000   0.00000   1.00000
   0.31416   0.30902   0.95106   0.30902   1.95106
   0.62832   0.58779   0.80902   0.89681   2.76008
   0.94248   0.80902   0.58779   1.70583   3.34787
   1.25664   0.95106   0.30902   2.65689   3.65689
   1.57080   1.00000   0.00000   3.65689   3.65689
   1.88496   0.95106  -0.30902   4.60795   3.34787
   2.19911   0.80902  -0.58779   5.41697   2.76008
   2.51327   0.58779  -0.80902   6.00476   1.95106
   2.82743   0.30902  -0.95106   6.31378   1.00000
   3.14159   0.00000  -1.00000   6.31378   0.00000
sum1= 6.313780000000001   sum2= 0.0


s1="""You are a student
of THUPHYS.
You should check
your tmail everyday.
You work hard
to earn good grade."""
s2=s1.replace('\n',' ') #將換行符號用空格取代
print ('s2:\n',s2)
s3=s2.split('.')  #以句點做分割符號
print ('s3:\n',s3)
s4=[]
for i in s3:
    if(len(i) < 1): continue  #==移除掉空字串
    i1=i.lstrip()
    s4.append(i1+'!')
    print (i1+'!')
print ('s4:\n',s4)
#join把這個列表轉換成為一個單一字串
newstr=' YES! '.join(s4)+' YES, I will.'
print ('newstr:\n',newstr)


s2:
 You are a student of THUPHYS. You should check your t
mail everyday. You work hard to earn good grade.
s3:
 ['You are a student of THUPHYS', ' You should check y
our tmail everyday', ' You work hard to earn good grad
e', '']
You are a student of THUPHYS!
You should check your tmail everyday!
You work hard to earn good grade!
s4:
 ['You are a student of THUPHYS!', 'You should check y
our tmail everyday!', 'You work hard to earn good grad
e!']
newstr:
 You are a student of THUPHYS! YES! You should check y
our tmail everyday! YES! You work hard to earn good gr
ade! YES, I will.

下面我們有一個問題要讓同學們來練習。s1這個字串是包括了x跟y的數據，我們要為這些二維平面上的數據點找一條直線，能夠適當的通過這些點來表徵這些點的分佈。假設這條直線的方程式為：\[y=mx+3\] 我們的目標就是要找到這個適當的斜率m給出最小的誤差。在典型的分析方法之中誤差的定義為點的y座標(\(y(i)\))到直線y座標(\(Y(i)\))之間的距離的平方和 \[Error=\sum_i (y(i)-Y(i))^2 \]。解決這個問題與前面的範例程式一樣，你要先把字串變成浮點數，在開始對浮點數做運算，為了要找到最適當的斜率m，你必須嘗試不同的m值。

s1="""
   10.00     8.04
    8.00     6.95
   13.00     7.58
    9.00     8.81
   11.00     8.33
   14.00     9.96
    6.00     7.24
    4.00     4.26
   12.00    10.84
    7.00     4.82
    5.00     5.68
   """

PYTHON程式語言的學習-4