- 圓環與直線
- 三維球
- 3維向量
- 正交曲線座標系統
- 三維等位面與法線
- 莫凡PYTHON MATPLOT 3D web page 莫凡PYTHON MATPLOT 3D
- 1. 首先在進行 3D Plot 時除了導入 matplotlib ,還要額外添加一個模塊,即 Axes 3D 3D 坐標軸顯示:
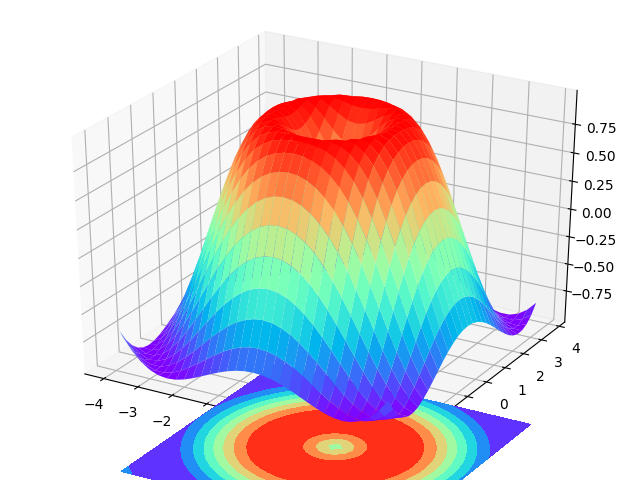
- 2. 接下來給進 X 和 Y 值,並將 X 和 Y 編織成柵格。每一個(X, Y)點對應的高度值我們用下面這個函數來計算。使用ax.plot_surface繪出網格表面圖形,並將一個 colormap rainbow 填充顏色。
- 3.將三維圖像投影到 XY 平面上做一個等高線圖。
matplot畫圖程式庫3D
圓環與直線 |
import matplotlib
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
matplotlib.use("Agg")
import numpy as np
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.set_aspect("equal")
# draw ring
p = np.mgrid[0:2.*np.pi:20j]
x = 3.*np.cos(p)*np.sin(np.pi/6.)
y = 3.*np.sin(p)*np.sin(np.pi/6.)
z = 3.*np.cos(np.pi/6.)
ax.plot(x, y, z, color="r")
ax.plot(p/3., p/3., p/3., color="b")
plt.savefig("matplot-3D-1.png")
print ('plot is done')
|
 |
三維球 |
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.set_aspect("equal")
# draw sphere
u, v = np.mgrid[0:2*np.pi:20j, 0:np.pi:10j]
x = np.cos(u)*np.sin(v)
y = np.sin(u)*np.sin(v)
z = np.cos(v)
ax.plot_wireframe(x, y, z, color="r")
# draw a point
xs=np.array([0,0,0,1])
ys=np.array([0,0,1,1])
zs=np.array([0,1,1,1])
ax.scatter(xs,ys,zs,color="y", s=100)
# draw a vector
ax.quiver(0,0,1,1,1,0,color='k')
ax.quiver(0,0,0,1,1,1,color='b',arrow_length_ratio = 0.1)
ax.set_xlabel('x', fontsize=15)
ax.set_ylabel('y', fontsize=15)
ax.set_zlabel('z', fontsize=15)
plt.savefig('3D-sphere.png')
|
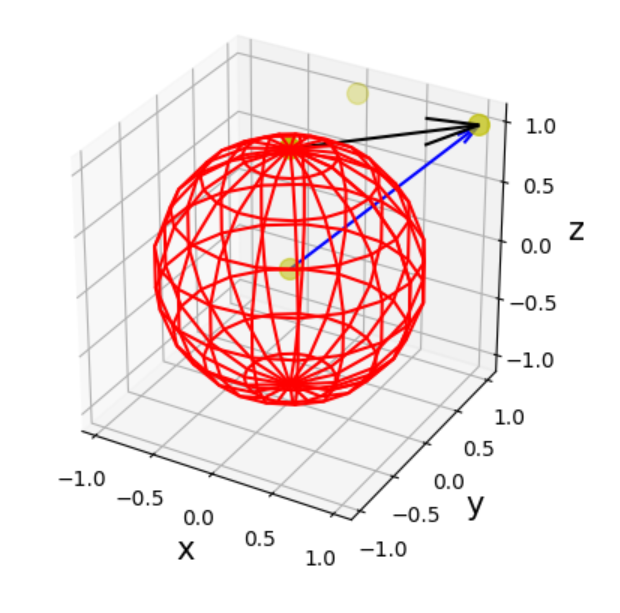 |
3D quiver |
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.set_aspect("equal")
v1=np.array([2,0,0])
v2=np.array([0,4,0])
v3=np.array([0,0,3])
v12=v1+v2
v123=v1+v2+v3
print('v12=',v12)
print('v123=',v123)
print('|v123|=',np.linalg.norm(v123))
phi=np.arctan(3/np.linalg.norm(v123))
print('phi=',phi,np.degrees(phi))
#ax.grid(True)
ax.quiver(-4,0,0,8,0,0,color='g',arrow_length_ratio = 0.05)
ax.quiver(0,-4,0,0,8,0,color='g',arrow_length_ratio = 0.05)
ax.quiver(0,0,-4,0,0,8,color='g',arrow_length_ratio = 0.05)
ax.scatter(0,0,0,'o')
ax.scatter(v1[0],v1[1],v1[2],'o')
ax.scatter(v1[0]+v2[0],v1[1]+v2[1],v1[2]+v2[2],'o')
ax.scatter(v1[0]+v2[0]+v3[0],v1[1]+v2[1]+v3[1],v1[2]+v2[2]+v3[2],'o')
ax.quiver(0,0,0,v1[0],v1[1],v1[2],color='b')
ax.quiver(v1[0],v1[1],v1[2],v2[0],v2[1],v2[2],color='b')
ax.quiver(v12[0],v12[1],v12[2],v3[0],v3[1],v3[2],color='b')
ax.quiver(0,0,0,v12[0],v12[1],v12[2],color='r',arrow_length_ratio = 0.1)
ax.quiver(0,0,0,v123[0],v123[1],v123[2],color='r',arrow_length_ratio = 0.1)
plt.savefig("3-vectors.png")
print ('plot is done')
|
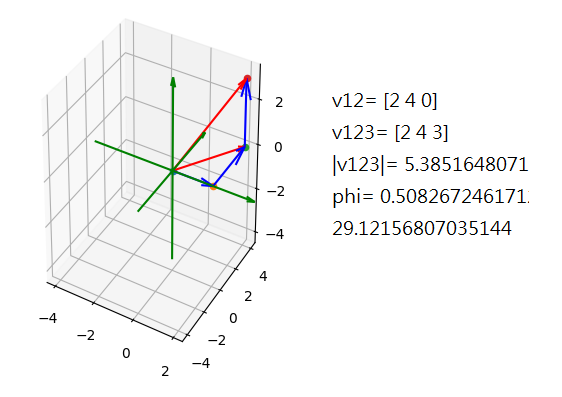 |
球座標當中的三個曲面交出三條曲線,這三個曲線形成了廣義的正交曲線座標系統(generalized orthonormal curved coordinates) |
import matplotlib
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
matplotlib.use("Agg")
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.set_aspect("equal")
# draw 3 surfaces
r=1. #r=constant
f,t= np.mgrid[0:2*np.pi:40j, 0:np.pi/2:40j]
x = r*np.cos(f)*np.sin(t)
y = r*np.sin(f)*np.sin(t)
z = r*np.cos(t)
ax.set_xlim(-1,1)
ax.set_ylim(-1,1)
ax.set_zlim(0,2)
ax.plot_surface(x,y,z, alpha=0.5, color='r')
t=np.pi/4. #theta=constant
r,f=np.mgrid[0:1.5:40j, 0:2.*np.pi:40j]
x=r*np.sin(t)*np.cos(f)
y=r*np.sin(t)*np.sin(f)
z=r*np.cos(t)
ax.plot_surface(x,y,z, alpha=0.3, color='g')
f=np.pi/4. #phi=constant
r,t=np.mgrid[0:1.2:40j, 0:np.pi/2.:40j]
x=r*np.sin(t)*np.cos(f)
y=r*np.sin(t)*np.sin(f)
z=r*np.cos(t)
ax.plot_surface(x,y,z, alpha=0.5, color='b')
# intersection curves
t=np.pi/4.
f=np.pi/4.
r=np.linspace(0,1.2,40)
x=r*np.sin(t)*np.cos(f)
y=r*np.sin(t)*np.sin(f)
z=r*np.cos(t)
ax.plot(x, y, z, color="k", lw=4)
r=1.
t=np.pi/4.
f=np.linspace(0,2.*np.pi,40)
x=r*np.sin(t)*np.cos(f)
y=r*np.sin(t)*np.sin(f)
z=r*np.cos(t)
ax.plot(x, y, z, color="k", lw=4)
r=1.
f=np.pi/4.
t=np.linspace(0,np.pi/2,40)
x=r*np.sin(t)*np.cos(f)
y=r*np.sin(t)*np.sin(f)
z=r*np.cos(t)
ax.plot(x, y, z, color="k", lw=4)
ax.set_title(r"3 surfaces $r=1, \theta=\pi/4, \phi=\pi/4$" \
" meet in 3 curves", fontsize=15)
ax.set_xlabel('x', fontsize=15)
ax.set_ylabel('y', fontsize=15)
ax.set_zlabel('z', fontsize=15)
plt.savefig("3-surfaces-spherical-intersec-curves.png")
print ('plot is done')
|
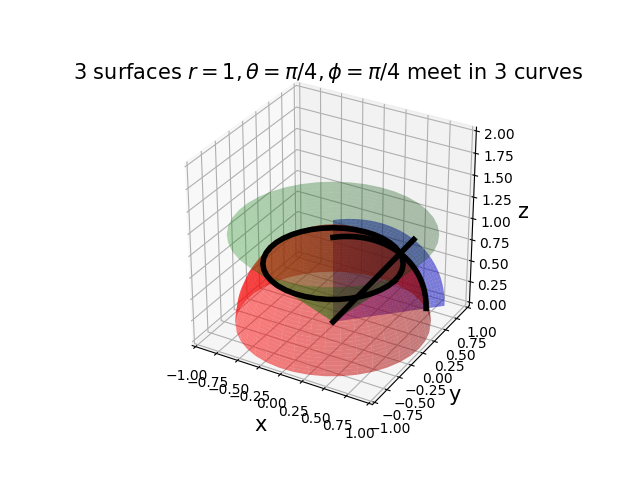 |
三維等位面與法線 |
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
fig = plt.figure()
ax = fig.gca(projection='3d')
x=np.linspace(2.,5.,10)
y=np.linspace(2.,5.,10)
X,Y=np.meshgrid(x,y)
Z=np.sqrt(X**2+Y**2)
Z2=np.sqrt(X**2+Y**2-6.)
Z3=np.sqrt(X**2+Y**2-12.)
ax.scatter([3], [4], [5], color="k", s=40)
ax.set_aspect("equal")
ax.plot_surface(X, Y, Z, label='C=0')
ax.plot_surface(X, Y, Z2, label='C=6')
ax.plot_surface(X, Y, Z3, label='C=12')
ax.quiver(3.,4.,5.,6./5.,8./5.,-10./5.,color='b')
ax.set_title("$f(x,y,z)=x^2+y^2-z=C$", fontsize=15)
#ax.plot_surface(X, Y, Z)
ax.set_xlabel('x', fontsize=15)
ax.set_ylabel('y', fontsize=15)
ax.set_zlabel('z', fontsize=15)
#ax.legend()
plt.show()
|
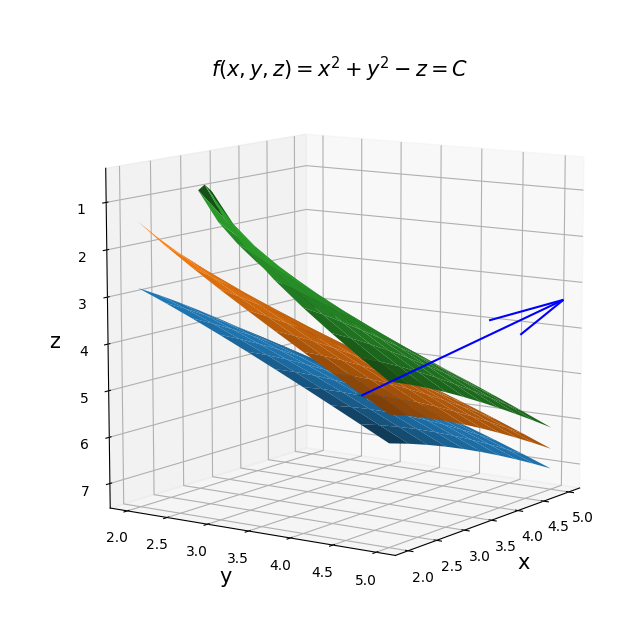 |
3D基本操作 |
import matplotlib
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
matplotlib.use("Agg")
# X, Y value
X = np.arange(-4, 4, 0.25)
Y = np.arange(-4, 4, 0.25)
X, Y = np.meshgrid(X, Y) # x-y 平面的网格
R = np.sqrt(X ** 2 + Y ** 2)
# height value
Z = np.sin(R)
ax.plot_surface(X, Y, Z, rstride=5, cstride=5, cmap=plt.get_cmap('rainbow'))
ax.contourf(X, Y, Z, zdir='z', offset=-2, cmap=plt.get_cmap('rainbow'))
其中,rstride 和 cstride 分別代表 row 和 column 的跨度。
可比較兩個圖分別是跨度為1 和 5 的效果。
以下為完整的程式:
=========================
import matplotlib
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
matplotlib.use("Agg")
fig = plt.figure()
ax = Axes3D(fig)
# X, Y value
X = np.arange(-4, 4, 0.25)
Y = np.arange(-4, 4, 0.25)
X, Y = np.meshgrid(X, Y) # x-y 平面的网格
R = np.sqrt(X ** 2 + Y ** 2)
# height value
Z = np.sin(R)
ax.plot_surface(X, Y, Z, rstride=5, cstride=5, cmap=plt.get_cmap('rainbow'))
ax.contourf(X, Y, Z, zdir='z', offset=-2, cmap=plt.get_cmap('rainbow'))
plt.savefig("mat-3D-mv1.png")
print ('plot is done')
|
|