檔案的寫出和檔案內容的讀入

1. \(U(x)=1/2 k x^2\)等間隔分割並且作函數求和

我們在範圍\((0,2)\)之間切割了10等份，對每一個\(x\)我們計算出位能函數的數值\(U=5x^2\)，然後對所有這11個\(U\)求和，就可以得到最後的結果\(S=77.0\)。我們也知道如果把每一個\(U\)乘以間隔的寬度\(dx=\dfrac{2}{10}=0.2\)，那麼最後的結果\(S dx\)可看成是曲線\(U(x=5x^2\)下的面積的近似。另一方面我們可以透過積分得到 (0,2)之間的積分結果： \[\int_0^2 5x^2 dx=\dfrac{5}{3}x^3|_0^2=\dfrac{5}{3}(8)=13.3333\] 我們可以與有限切割的數值做比較，可以預期的當切割的分數越來越大時，誤差就會越來越小。

k=10; a=0; b=2; N=10; dx=(b-a)/N; S=0
for i in range(N+1):
    x=a+dx*i
    U=1/2*k*x**2
    S+=U
    print('{:4d} {:10.3f} {:10.3f} {:10.3f}'.format(i,x,U,S))
print('S=',round(S,3),'  S*dx=',round(S*dx,3),
'  S_integ=',round(1/2*k*2**3/3,3))

   0      0.000      0.000      0.000
   1      0.200      0.200      0.200
   2      0.400      0.800      1.000
   3      0.600      1.800      2.800
   4      0.800      3.200      6.000
   5      1.000      5.000     11.000
   6      1.200      7.200     18.200
   7      1.400      9.800     28.000
   8      1.600     12.800     40.800
   9      1.800     16.200     57.000
  10      2.000     20.000     77.000
S= 77.0   S*dx= 15.4   S_integ= 13.333




---




2. 將位能函數的數據寫入一個檔案當中

FW=open('Ux-data.txt','w')
k=10; a=0; b=2; N=10; dx=(b-a)/N; S=0
for i in range(N+1):
    x=a+dx*i
    U=1/2*k*x**2
    S+=U
    s='{:4d} {:10.3f} {:10.3f} {:10.3f}'.format(i,x,U,S)
    FW.write(s+'\n')
    print(s)
FW.close()
print('FILE written and closed')

   0      0.000      0.000      0.000
   1      0.200      0.200      0.200
   2      0.400      0.800      1.000
   3      0.600      1.800      2.800
   4      0.800      3.200      6.000
   5      1.000      5.000     11.000
   6      1.200      7.200     18.200
   7      1.400      9.800     28.000
   8      1.600     12.800     40.800
   9      1.800     16.200     57.000
  10      2.000     20.000     77.000
FILE written and closed




---




3. 從一個檔案讀入位能的數據

FR=open('Ux-data.txt','r')
a=FR.read()
print('a')
print(a)
b=a.split()
print('b')
print(b)

a
   0      0.000      0.000      0.000
   1      0.200      0.200      0.200
   2      0.400      0.800      1.000
   3      0.600      1.800      2.800
   4      0.800      3.200      6.000
   5      1.000      5.000     11.000
   6      1.200      7.200     18.200
   7      1.400      9.800     28.000
   8      1.600     12.800     40.800
   9      1.800     16.200     57.000
  10      2.000     20.000     77.000
b
['0', '0.000', '0.000', '0.000', '1', '0.200', '0.200', '0.200', '2', '0.400', '0.800', '1.000', '3', 
'0.600', '1.800', '2.800', '4', '0.800', '3.200', '6.000', '5', '1.000', '5.000', '11.000', '6', '1.20
0', '7.200', '18.200', '7', '1.400', '9.800', '28.000', '8', '1.600', '12.800', '40.800', '9', '1.800'
, '16.200', '57.000', '10', '2.000', '20.000', '77.000']




---




4. 將字串轉換為浮點數

FR=open('Ux-data.txt','r')
a=FR.read()
b=a.split()
print('b=',b)
NC=4
NR=int(len(b)/NC)
x=[]; U=[]; S=[]
for i in range(NR):
    xi=float(b[i*NC+1])
    Ui=float(b[i*NC+2])
    Si=float(b[i*NC+3])
    x.append(xi)
    U.append(Ui)
    S.append(Si)
print('x=',x)
print('U=',U)
print('S=',S)

b= ['0', '0.000', '0.000', '0.000', '1', '0.200', '0.200', '0.200', '2', '0.400', '0.800', '1.000', '3
', '0.600', '1.800', '2.800', '4', '0.800', '3.200', '6.000', '5', '1.000', '5.000', '11.000', '6', '1
.200', '7.200', '18.200', '7', '1.400', '9.800', '28.000', '8', '1.600', '12.800', '40.800', '9', '1.8
00', '16.200', '57.000', '10', '2.000', '20.000', '77.000']
x= [0.0, 0.2, 0.4, 0.6, 0.8, 1.0, 1.2, 1.4, 1.6, 1.8, 2.0]
U= [0.0, 0.2, 0.8, 1.8, 3.2, 5.0, 7.2, 9.8, 12.8, 16.2, 20.0]
S= [0.0, 0.2, 1.0, 2.8, 6.0, 11.0, 18.2, 28.0, 40.8, 57.0, 77.0]




---




5. 利用函數副程式將字串所含的二維數據轉換成為浮點數二維列表

在數據分析當中我們會經常遇到從檔案當中讀取數據，這樣的數據就像我們常見的Excel當中的數據一樣是二維結構的數據(MxN，N行M列的二維數據)。我們可以先建立一個函數副程式，將這樣結構的一維字串列表轉換成一個二維浮點數列表，新列表中的元素都已經從字串轉換成為浮點數，可以方便做後續的數據分析。在這個程式當中就試圖利用strdata()這個副程式，將從外部檔案(Ux-data.txt)讀入的字串列表b，做適當的轉換得到浮點數的列表data。data是M個列表所成的列表(所以稱為二維列表)，每一個子列表當中都有N個浮點數。

def strdata(b,NC,NR):
    data=[[] for i in range(NR)]
    for i in range(NR):
        for j in range(NC):
            data[i].append(float(b[i*NC+j]))
    return data

FR=open('Ux-data.txt','r')
C=FR.readline(); FR.seek(0); NC=len(C.split())
a=FR.read(); b=a.split()
NR=int(len(b)/NC)
data=strdata(b,NC,NR)
for i in range(NR):
    print(data[i])

6. 位能函數與保守力的作圖(折返點、平衡點)

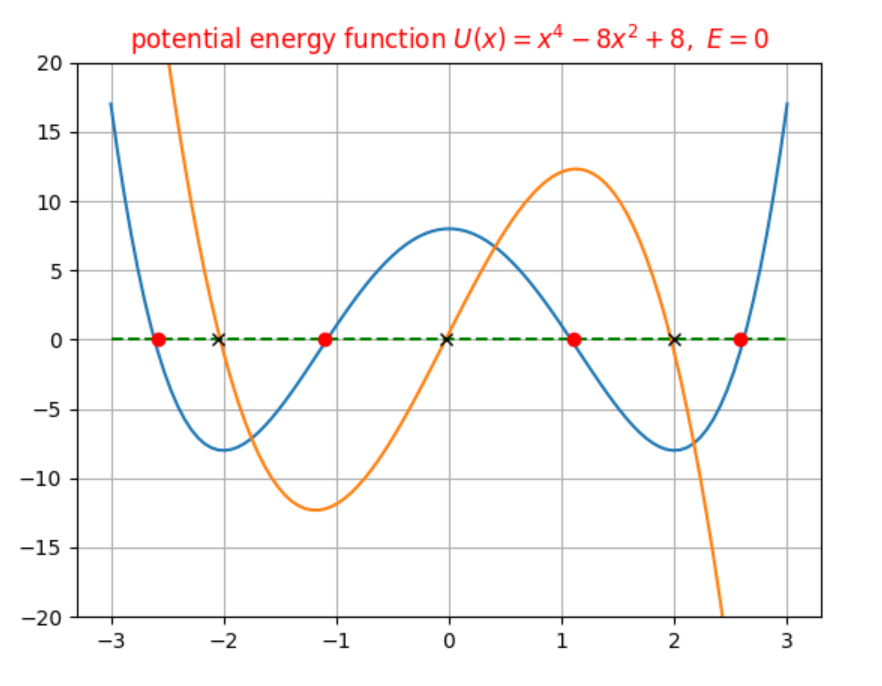在一維空間中給定了一個位能函數\(U(x)\)就可以透過微分關係\(F(x)=-\dfrac{dU(x)}{dx}\)得到與這個位能函數對應的保守力\(F(x)\)，因此保守力也會是一個位置的函數。如果我們再給定一個粒子在這一維空間上運動的力學能\(E\)，那麼根據力學能守恆，我們還可以決定粒子在一維空間中，受到這個保守力的作用會在哪些位置發生折返點的現象。判斷折返點的條件由速度\(v=0\)，動能\(K=0\)決定，也就是位能等於力學能，\(U(x)=E\)。在我們下面的應用中，希望同學們可以將位能函數畫出來，也利用差分近似，也可以畫出保守力對位置的函數圖，並且利用迴圈計算折返點的位置。其做法如下。


---




import math
import matplotlib
import matplotlib.pyplot as plt
pi=math.pi
sqrt=math.sqrt
fm=['{:10d}','{:10.4f}'*1,'{:10.4f}'*2,'{:10.4f}'*3,'{:10.4f}'*4,'{:10.4f}'*5,
'{:10.4f}'*6,'{:10.4f}'*7]

a=-3; b=3; N=101; E=0
dx=(b-a)/N; Lx=[]; LU=[]; LF=[]
for i in range(N+1):
    x=a+dx*i
    U=x**4-8*x**2+8
    Lx.append(x)
    LU.append(U)
ii=0; n=0
for i in range(N):
    F=-(LU[i+1]-LU[i])/dx
    LF.append(F)
def root(L,x,E):
    N=len(L)
    D=[]
    for i in range(N):
        D.append(abs(L[i]-E))
    R=[]
    for i in range(1,N-1):
        if(D[i] < D[i-1] and D[i] < D[i+1]):
            R.append(x[i])
    return R
RU=root(LU,Lx,E)
RF=root(LF,Lx,0)
print('RU=',RU)
print('RF=',RF)
plt.plot(Lx,LU)
plt.plot(Lx[:-1],LF)
plt.plot([a,b],[E,E],'g--')
plt.plot(RU,[E for i in range(len(RU))],'ro')
plt.plot(RF,[E for i in range(len(RF))],'kx')
plt.ylim(-20,20)
plt.title('potential energy function $U(x)=x^4 - 8x^2 +8, \,\, E=0$', color='red', fontsize=12)
plt.grid()
plt.savefig("Ux-F1.png")
print('done')

RU= [-2.5841584158415842, -1.099009900990099, 1.099009900990099, 2.584158415841584]
RF= [-2.0495049504950495, -0.02970297029702973, 1.99009900990099]
done




---





---