電荷在電場中的運動

本單元的程式

PS-EM-01.py
PS-EM-02.py
PS-EM-03.py

本單元的解說影片

在這個單元中我們要利用vpython的動畫模擬來呈現電荷在電場中的運動。

  1. 電子在帶正電的點電荷電場中運動

    2.
    一個帶負電的電子在一個正電荷的作用下，其運動的方式就像行星在太陽的重力吸引下進行軌道運動，因為靜電力(就是所謂的庫倫力)與重力一樣，都是一種向心力並且其大小與距離的平方成反比。下面的程式中有一個點電荷所產生電場的函數(EF_point)，在主程式中我們把電子的電荷量乘上電場的大小就是庫倫力\[\vec{F}=q_e \vec{E}; \,\,\, \vec{a}=\vec{F}/m_e，\] \[\vec{E}=\dfrac{k q q_e}{\mathscr{r}^2} \hat{\mathscr{r}}\] \[\vec{\mathscr{r}}=\vec{r}-\vec{r_q}\] \(m_e, \, q_e, \, \vec{r}\)分別是電子的質量、帶電量和位置向量。再利用差分近似我們可以隨著時間演進，更新電子的速度和電子的位置：
    \[ \vec{v}(t+dt) \simeq \vec{v}(t)+\frac{\vec{F}}{m_e}dt \,\, \leftarrow \,\, \vec{a}=\vec{F}/m_e\] \[ \vec{r}(t+dt) \simeq \vec{r}(t)+\vec{v}(t)dt \] 
    Web VPython 3.2
def EF_point(q,rq,r):
    ke=1.
    rrq=r-rq
    rrq0=mag(rrq)
    E=ke*q*rrq/rrq0**3
    return E
    
q=1.; rq=vec(0,3,0)
scene = display(width=600, height=600, center=vec(0, 4, 0),
                background=vec(0,0,0))    
Xaxis=arrow(pos=vec(-4,0,0),axis=vec(8,0,0),shaftwidth=0.01 \ 
       ,headwidth=0.02)
Yaxis=arrow(pos=vec(0,0,0),axis=vec(0,8,0),shaftwidth=0.01 \
       ,headwidth=0.02)
charge = sphere(pos=rq, radius=0.2, color=color.red)
qe=-1.; me=1.; xe=-2; ve=0.5
e = sphere(pos=vec(xe,0,0), radius=0.1, color=color.cyan, \ 
    make_trail=True, retain=500, trail_radius=0.02)
e.v=vec(ve,0,0)
t=0.; dt=0.01; NR=int(1/dt)
scene.camera.pos=vec(0,4,12)
scene.pause('click')
while t < 100:
    rate(NR*4)
    E=EF_point(q,rq,e.pos)
    e.v+=qe*E/me*dt
    e.pos+=e.v*dt
    t+=dt



    glowscript(PS-EM-01.py)




  2. 電子在帶正電的圓環中進行簡諧運動

    3.
    帶正電的圓環在通過圓心的中垂線上所產生的電場，是向著圓心的方向並且其大小與距離圓心的大小約略是正比關係，因此電力對電子的作用就像彈力(F=-kx)的作用一樣，因此電子在圓環上的正電荷的作用下進行簡諧運動。 
    Web VPython 3.2
# 帶負電的電子受到一個圓環上16\n個正電荷的吸引而進行簡諧運動 \
# qe=-1, me=1, 電子初始的位置x0=1, \n正電荷q=1, 圓環的半徑R=1'
def EF_ring_q(Nq,q,rq,R,r):
    k=1.
    E=vec(0.,0.,0.)
    for i in range(Nq):
        t=2.*pi/Nq*i
        rrp=r-rq[i]
        rrp0=mag(rrp)
        E=E+k*q*rrp/rrp0**3
    return E
    
Nq=16; q=1.; R=1. 
scene = display(width=800, height=800, center=vec(0, 0, 0),
                background=vec(0,0,0))    
arr=arrow(pos=vec(-2,0,0),axis=vec(4,0,0),shaftwidth=0.01, \
    headwidth=0.02,color=vec(1,1,1))
scene.camera.pos=vec(1,0,6)
rq=[]
for i in range(Nq):
    t=2.*pi/Nq*i
    rq.append(vec(0,R*cos(t),R*sin(t)))
    ball = sphere(pos=rq[i], radius=0.1, color=color.red)
qe=-1.; me=1.; x0=1.
e = sphere(pos=vec(x0,0,0), radius=0.1, color=color.blue)
E=EF_ring_q(Nq,q,rq,R,e.pos)
ss='帶負電的電子受到一個圓環上16\n個正電荷的吸引而進行簡諧運動 \
\n qe=-1, me=1, 電子初始的位置x0=1, \n正電荷q=1, 圓環的半徑R=1'
T=label(text=ss,pos=vector(0,3,0),height=20)
scene.pause('click')
e.v=vec(0,0,0)
t=0.; dt=0.01; NR=int(1/dt)
while t < 20:
    rate(NR)
    E=EF_ring_q(Nq,q,rq,R,e.pos)
    e.v+=qe*E/me*dt
    e.pos+=e.v*dt
    t+=dt



    glowscript(PS-EM-02.py)




  3. 電荷在平行板的電場中運動

    4.
    帶電的平行電板所提供的電場是均勻的電場，電荷在平行電板中受到定力的作用，因此會產生等加速度運動，就像在均勻的重力場下，其運動的軌跡是拋物線。但是在我們的模擬當中我們利用下面這個指令，將電荷的帶電量做q[i]=sin(0.2*i)函數的週期性的變化，因此在平行電板的偏折下會週期性的向上或向下偏折。我們讓屏幕做等速度的移動(plate5.pos.z += vp*dt)，就可以在屏幕上觀察到電荷上下擺動的週期性運動。 
    Web VPython 3.2
N=160; L1=5; d=2; L2=25
scene = canvas(width=800, height=600, background=vec(0.2,0.2,0.2)) 
X=arrow(pos=vec(0,0,0),axis=vec(27,0,0),shaftwidth=0.1,color=vec(1,1,0))
Y=arrow(pos=vec(0,0,0),axis=vec(0,8,0),shaftwidth=0.1,color=vec(0,0,1))
Z=arrow(pos=vec(0,0,0),axis=vec(0,0,8),shaftwidth=0.1,color=vec(1,1,1))
X.headwidth=0.1; Y.headwidth=0.1; Z.headwidth=0.1;
plate1=box(pos=vec(L1/2.,-d,0),size=vec(L1,0.1,L1), color=color.blue)
plate2=box(pos=vec(L1/2.,d,0),size=vec(L1,0.1,L1), color=color.blue)
screen=box(pos=vec(L2,0,-20),size=vec(0.1,20,40), color=color.cyan)
gun=cylinder(radius=0.6,pos=vec(-2,0,0),axis=vec(2,0,0))
balls=[sphere(pos=vec(0.1,0,0),radius=0.2,color=color.red) for i in range(N)]
vx=4.
vp=1.
ay0=0.5
vy=[0. for i in range(N)]
ay=[0. for i in range(N)]
q0=1.0
q=[q0*sin(0.2*i) for i in range(N)]
t,dt=0.,0.01; NR=int(1./dt)
scene.forward=vec(cos(-pi/6),0,sin(-pi/6))
print(t,scene.camera.pos,scene.forward,scene.center)
scene.pause('click')
while t < 30.:
    rate(NR)
    screen.pos.z += vp*dt
    for i in range(N):  
        if(t < 0.15*i):  continue
        if(balls[i].pos.x >= 0.) and (balls[i].pos.x < 10.): ay[i]=q[i]*ay0
        else:   ay[i]=0.
        if(balls[i].pos.x > 25.):
            balls[i].color=color.blue
            balls[i].pos.z += vp*dt
            continue
        vy[i] += ay[i]*dt
        balls[i].pos.y += vy[i]*dt        
        balls[i].pos.x += vx*dt
    t += dt
print(t,scene.camera.pos,scene.forward,scene.center)



    glowscript(PS-EM-03.py)




  4. 陰極射線管

    5.
    電子從電子槍射出來之後在飛經兩個互相垂直的平行電板所提供的電場作用下，會在兩個垂直方向上被偏折，因此隨著兩個電場的大小週期性變化，就可以將電子偏移射在屏幕的各個區域。 
    Web VPython 3.2
scene = canvas(width=800, height=800,center=vec(10,0,0), \
background=vec(0.2,0.2,0.2), forward=vec(0.5,0,-1))
arrx=arrow(pos=vec(0,0,0),axis=vec(8,0,0),shaftwidth=0.05, \
    color=vec(1,1,0))
arrY=arrow(pos=vec(0,0,0),axis=vec(0,8,0),shaftwidth=0.05, \
    color=vec(0,0,1))
arrZ=arrow(pos=vec(0,0,0),axis=vec(0,0,8),shaftwidth=0.05, \
    color=vec(1,1,1))
N=250; L1=5; L2=25; d=2; R=0.1
balls = [sphere(pos=vec(-2,0,0), radius=R, color=color.red) \
    for i in range(N)]
plate1=box(pos=vec(L1/2.,-d,0),size=vec(L1,0.1,L1), \ 
    color=color.blue, opacity=0.3)
plate2=box(pos=vec(L1/2.,d,0),size=vec(L1,0.1,L1), \ 
    color=color.blue, opacity=0.3)
plate3=box(pos=vec(L1*1.5+L1/2.,0,-d),size=vec(L1,L1,0.1), \
    color=color.green, opacity=0.3)
plate4=box(pos=vec(L1*1.5+L1/2.,0,d),size=vec(L1,L1,0.1), \
    color=color.green, opacity=0.3)
plate5=box(pos=vec(L2,0,0),size=vec(0.1,20,20), \
    color=color.cyan)
gun=cylinder(radius=0.6,pos=vec(-2,0,0),axis=vec(2,0,0))
vx=4.
ay0=0.8
az0=6.0
vy=[0. for i in range(N)]
ay=[0. for i in range(N)]
vz=[0. for i in range(N)]
az=[0. for i in range(N)]
T=4.
t,dt=0.,0.01; NR=int(1./dt)
scene.pause('click')
while t < 100.:
    rate(NR)
    for i in range(N):
        if(t < 0.05*i):  continue
        
        if(balls[i].pos.x > 0.) and (balls[i].pos.x < 10.): 
            ay[i]=ay0*sin(0.2*(t-0.5)+pi/2.)
        else:   ay[i]=0.
        if(balls[i].pos.x > 25-R):   continue
        vy[i] += ay[i]*dt
        balls[i].pos.y += vy[i]*dt
        
        if(balls[i].pos.x > 1.5*L1) and (balls[i].pos.x < 2.5*L1): 
            az[i]=az0*sin(4.*t)
        else:   az[i]=0.
        if(balls[i].pos.x > 25.):   continue
        vz[i] += az[i]*dt
        balls[i].pos.z += vz[i]*dt
        
        balls[i].pos.x += vx*dt
    t += dt



    glowscript(PS-EM-04.py)




  5. 拉塞福的散射實驗

    6.
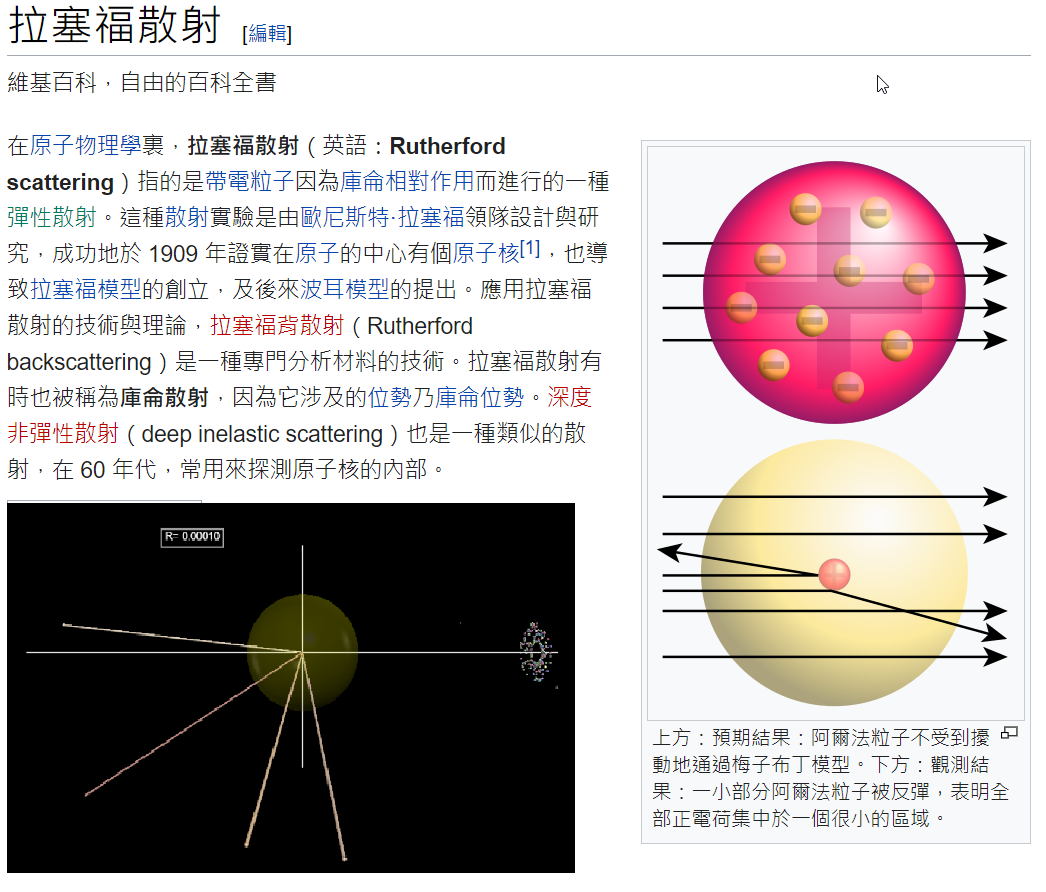
    這個習題希望同學們能夠利用我們在電學和運動模擬中所學到的經驗，來設計並體驗拉塞福在1909年非常著名的散射實驗，這個實驗被譽稱為20世紀最偉大物理實驗。 拉塞福散射(維基百科)

    GlowScript 3.2 VPython
def EF_point(q,rq,r):
    ke=1.
    rrq=r-rq
    rrq0=mag(rrq)
    E=ke*q*rrq/rrq0**3
    return E    
q=79; rq=vec(0,0,0)
scene = canvas(width=1000, height=700, center=vec(0, 0, 0))
Xaxis=arrow(pos=vec(-4,0,0),axis=vec(8,0,0),shaftwidth=0.01, \ 
     headwidth=0.02)
Yaxis=arrow(pos=vec(0,-1,0),axis=vec(0,2,0),shaftwidth=0.01)
charge = sphere(pos=rq, radius=0.03, color=color.red)
Na=21; qa=2.; ma=4.; xa=-2; va=60; Ly=0.2; Ly2=Ly/2; dy=Ly/Na
qc=[qa for i in range(Na)]
es = [sphere(pos=vec(-2,-Ly2+dy*i,0), radius=0.03, \ 
   color=vec(0.5+0.5*random(),0.5+0.5*random(),0.5+0.5*random()), 
    make_trail=True) for i in range(Na)]
for i in range(Na):
    es[i].v=vec(va,0,0)
t=0.; dt=0.0002; NR=int(1/dt)
labva='va={:04.1f}'.format(va)
label(text=labva,pos=vector(-2,2,0))
print_options(width=1000, height=100)
print('q=',q,'  rq=',rq,'  Na=',Na,'  qa=',qa,'  ma=',ma, \
    '  xa=',xa,'  va=',va,'  Ly=',Ly)
scene.waitfor('click')
while t < 10:
    rate(NR/100)
    for i in range(Na):
        if(mag(es[i].pos) > 2.2): break
        E=EF_point(q,rq,es[i].pos)
        es[i].v+=qc[i]*E/ma*dt
        es[i].pos+=es[i].v*dt
    t+=dt



    glowscript(PS-EM-05.py)