電場電通量與高斯定律

本單元的程式

PS-Gauss-01.py
PS-Gauss-02.py
PS-Gauss-03.py

本單元的解說影片

電通量

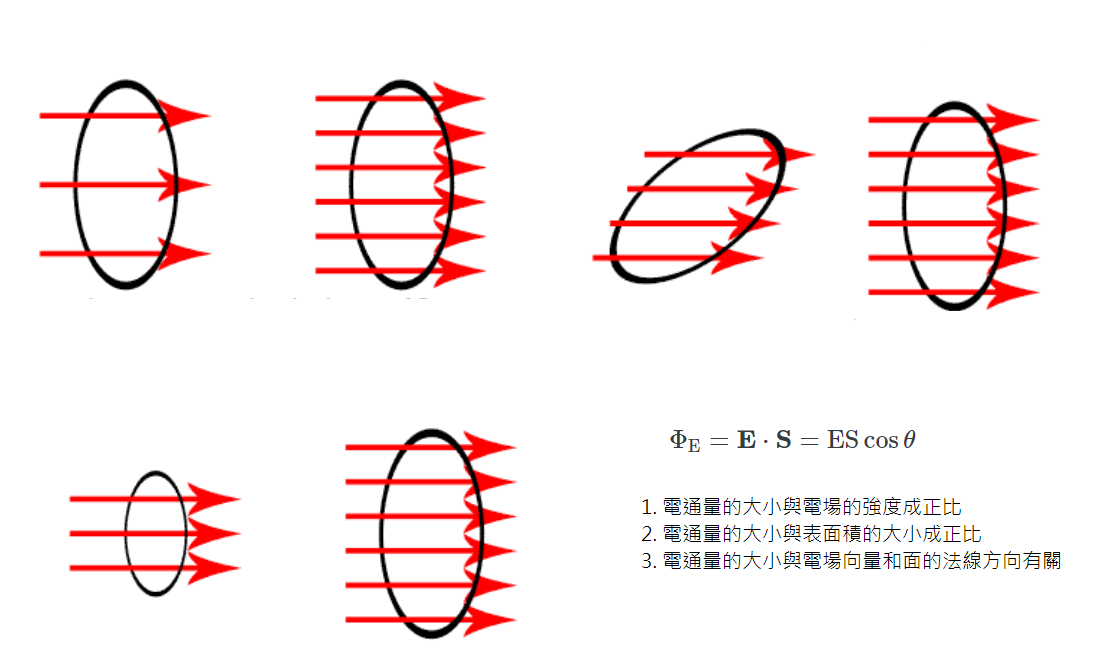
在這個單元中我們要利用vpython的動畫模擬來呈現電荷在電場中的運動。 電荷的周圍充斥著電場。若以圖形表示，該電場可以被表示為從一個點（電荷）散開的輻射線，稱為電場線或電力線。而這些線的密度與電場強度呈正相關，稱為電通量密度，也就是每單位面積的電力線數目。因此，電通量與穿過表面的電場線的總數成正比。為了簡化計算，通常在計算上會選取垂直於電力線的表面。如果電場為一均勻電場，則通過所選面積 \( \mathbf {S} \) 的表面的通量為 \[ \Phi_{E}=\mathbf{E} \cdot \mathbf{S} =ES \cos \theta \] 其中\( \mathbf{E} \)為電場（單位為 V/m ）、\(E\)為電場強度、 \(S\) 為表面面積、 \( \theta\) 為電場線與 \(S\) 的法線之間的夾角。
  1. 電通量的大小與電場的強度成正比
  2. 電通量的大小與表面積的大小成正比
  3. 電通量的大小與電場和面的法線夾角有關
如果電場為一非均勻電場，則通常會將此一較大面積的電通量分割，改取一小塊面積 \( d\mathbf{S}\) 上的電通量 \(d\Phi_{E}\) \[ d\Phi_{E}=\mathbf{E} \cdot d\mathbf{S}\] （電場 \(\mathbf {E}\)乘以垂直於所選面積表面的分量）。因此，表面 \(S\) 上的電通量可由表面積分得到：
\(\Phi_{E}=\iint_{S} \mathbf{E} \cdot d\mathbf{S}\)
其中 \(\mathbf{E}\)是電場，\(d\mathbf{S}\)是閉合表面\(S\)上的微小面積，其方向定義為表面法線朝外。
根據高斯定律，通過任一封閉曲面（高斯面）的淨電通量(\(\Phi_{E}\))，必與該封閉曲面內所圍之淨電荷量(\( Q_{\rm{enc}}\))成正比。 而在真空中，此比例常數為一定值\( 1/\varepsilon_{0}\)。其數學式為 :
\(\Phi_{E}=\oint_{\scriptstyle{S}} \mathbf{E} \cdot d\mathbf{S} =\frac{Q_{\rm{enc}}}{\varepsilon_{0}} \)
其中 \(\mathbf{E}\)是電場、 \(S\) 是任一封閉曲面、 \( Q_{\rm {enc}}\) 是曲面 \(S\) 內的總淨電荷。\(\varepsilon_{0}\)是介電常數（為一通用常數，也稱為真空中電容率或真空介電常數 ）。\( \varepsilon _{0}\approx 8.854187817...\times 10^{-12}\) (F/m) 此一關係式以其積分形式被稱為電場高斯定律，是四個馬克士威方程式之一。電通量的單位為伏特米（V·m）。

  1. 畫出平面的方塊為電通量的計算做準備

    2.
    \(-R \le x \le R; \,\,\, -R \le z \le R; L=2R; R=1; 面積A=L^2=4\) 
    Web VPython 3.2
NL=4; L=4; L2=int(L/2); r=[];balls=[]; R1=0.1; R2=0.1; yc=L/2; D=3*L; ycc=3
cen=vec(0,yc,0)
scene=canvas(width=600, height=600, center=vec(0,2,0))
plane1=box(pos=cen,size=vec(L,0.01,L),color=vec(0,1,1))
cenp=sphere(pos=scene.center,radius=0.05,color=vec(1,1,1))
charge=sphere(pos=vec(0,0,0),radius=0.2,color=vec(0,1,0))
scene.forward=vec(-0.45, -0.31, -0.83)
print_options(width=400, height=600, readonly=False,digits=4,pos='right')
print(scene.forward,scene.camera.pos)
T1='在一個4x4的平面下方有一個點電荷\
    \n(黃色球)白色的球代表平面的中央點'
T2='點電荷在正方形所產生的電場由點電荷至\n正方形之間的向量決定(庫倫定律)'
T3='電場向量與正方形法線向量的內積決定了該正方形的電通量貢獻\
    \n橘色的箭頭是電場向量,紅色的箭頭是平面的法向量'
LB=label(text=T1,pos=vec(0,4.5,0))
for i in range(NL+1):
    a1=arrow(pos=cen+vec(-L2,0.03,-L2+i),axis=vec(L,0,0),\
       shaftwidth=0.02, headwidth=0.02, color=vec(0.2,0.2,0.2))
    a2=arrow(pos=cen+vec(-L2+i,0.03,-L2),axis=vec(0,0,L),\
       shaftwidth=0.02, headwidth=0.02, color=vec(0.2,0.2,0.2))
scene.pause('click-1')
LB.text=T2
eps0=1./(4*pi); E=[]; q=10
for i in range(NL):
    for j in range(NL):
        c0=vec(i-L2+0.5,L2,j-L2+0.5)
        arrow(pos=vec(0,0,0),axis=c0,shaftwidth=0.02,headwidth=0.02,\
           color=vec(1,1,1))
        sphere(pos=c0,radius=0.03,color=vec(1,0,0))
scene.pause('click-2')
scale=0.5
for i in range(NL):
    for j in range(NL):
        c0=vec(i-L2+0.5,L2,j-L2+0.5)
        v0=c0-charge.pos
        v0s=mag(v0)
        v1=q*hat(v0)/v0s**2*scale
        ar=arrow(pos=c0,axis=v1,shaftwidth=0.03,headwidth=0.03,\
           color=vec(1,0.5,0))
        sphere(pos=c0,radius=0.05,color=vec(1,0,0))
        E.append(ar)
scene.pause('click-3')
LB.text=T3
for i in range(NL):
    for j in range(NL):
        c0=vec(i-L2+0.5,L2,j-L2+0.5)
        v0=c0-charge.pos
        ar=arrow(pos=c0,axis=vec(0,0.5,0),shaftwidth=0.02,\
           headwidth=0.04,color=vec(1,0,0))
FLUX=0; area=(L/NL)**2; n=vec(0,1,0)
for v in E:
    fx=dot(v.axis/scale,n)*area
    FLUX+=fx
print('FLUX_1=',FLUX)



    glowscript(PS-Gauss-01A.py)




  2. 圓球曲面的電通量

    3.
    我們也可以選擇以球面作為我們電通量的考慮曲面，對於球面而言，我們可以採取球座標系統來描述我們的曲面。將曲面分割成為若干個小曲面，再針對每一個小曲面計算電場向量和法向量的內積，得到該曲面的電通量貢獻，最後加在一起就是整個曲面的電通量。在這個問題中我們先採取最簡單處理的方法，就是將點電荷放在球心，在這樣一個情況下曲面的法向量與電場向量是完全重疊的。這個程式當中我們還把上一個練習當中的正方形平面放進來，對兩個電通量比較。很明顯的可以看出來，由於問題的對稱性曲面的電通量會大於平面的電通量，原因非常簡單，就是上面所說的，法線向量的方向與電場的方向在同一條線上。當然另外一個次要因素是曲面的面積略大於正方形平面的面積。 
    Web VPython 3.2
def EF_point(q,rq,r):
    ke=1.
    rrq=r-rq
    rrq0=mag(rrq)
    Es=ke*q/rrq0**2
    E=ke*q*rrq/rrq0**3
    return E,Es
def plaq(jt,jf):
    f=df*(jf-0.5); t=dt*(jt-0.5)
    v1=RG*vec(cos(f)*sin(t),cos(t),sin(f)*sin(t))
    v2=RG*vec(cos(f+df)*sin(t),cos(t),sin(f+df)*sin(t))
    v3=RG*vec(cos(f)*sin(t+dt),cos(t+dt),sin(f)*sin(t+dt))
    v4=RG*vec(cos(f+df)*sin(t+dt),cos(t+dt),sin(f+df)*sin(t+dt))
    curve(pos=[v1,v2])
    curve(pos=[v1,v3])
    curve(pos=[v2,v4])
    curve(pos=[v4,v3])
    return

q1=10.; rq1=vec(0.,0.,0.); R=0.2; RG=R*10
scene=canvas(width=800, height=600, center=vector(0,0,0))
plane1=box(pos=vec(0,2,0),size=vec(4,0.02,4),color=vec(0,1,1))
print_options(width=500, height=600, readonly=False)
print_options(digits=4)
#print_options(pos='bottom')
print_options(pos='right')
scene.center=vector(0,0,0)
scene.range=4
#scene.camera.pos=vec(0,0,8); 
print('forward,cam,cen=',scene.forward,scene.camera.pos,scene.center,scene.range)

X=arrow(pos=vec(0,0,0),axis=vec(2,0,0),shaftwidth=0.02,headwidth=0.04,color=vec(1,1,0))
Y=arrow(pos=vec(0,0,0),axis=vec(0,2,0),shaftwidth=0.02,headwidth=0.04,color=vec(1,1,0))
Z=arrow(pos=vec(0,0,0),axis=vec(0,0,2),shaftwidth=0.02,headwidth=0.04,color=vec(1,1,0))
Q1=sphere(pos=rq1,radius=R,color=vec(1,0,0))
G=sphere(pos=rq1,radius=RG,color=vec(1,1,0), opacity=0.2)
T1='計算點電荷對圓球面的電通量'
LB=label(text=T1,pos=vec(0,-3,0))
Nt=8; Nf=16; NA=Nt*Nf; dA=4*pi*RG**2/NA
s=0.1; r1=vec(1,0,0); FLUX=0; dt=pi/Nt; df=2*pi/Nf
scene.pause('click-1: 分割成小曲面')
LB.text='將曲面分割成為若干個小曲面'
t0=pi/4
for jt in range(Nt):
    t=dt*jt
    if(t > t0): continue
    for jf in range(Nf):
        plaq(jt,jf)

print('cam,cen=',scene.camera.pos,scene.center)
scene.pause('click-2: Normal vectors')
LB.text='小曲面的法向量(red)'
for jt in range(Nt):
    t=dt*jt
    if(t > t0): continue
    for jf in range(Nf):
        f=df*jf
        r1=R*vec(cos(f)*sin(t),cos(t),sin(f)*sin(t))
        rG=RG*vec(cos(f)*sin(t),cos(t),sin(f)*sin(t))
        dS=hat(r1)*dA
        VN=arrow(pos=rG,axis=hat(r1)*0.5,shaftwidth=0.02,headwidth=0.04,color=vec(1,0,0))
        #VE=arrow(pos=rG,axis=E*0.5,shaftwidth=0.02,headwidth=0.04,color=vec(0,0.5,1))       

scene.pause('click-3 add E-field vectors')
LB.text='小曲面的電場向量(blue)'
for jt in range(Nt):
    t=dt*jt
    if(t > t0): continue
    for jf in range(Nf):
        f=df*jf
        r1=R*vec(cos(f)*sin(t),cos(t),sin(f)*sin(t))
        rG=RG*vec(cos(f)*sin(t),cos(t),sin(f)*sin(t))
        dS=hat(r1)*dA
        E,Es=EF_point(q1,rq1,rG)
        VE=arrow(pos=rG,axis=E*0.5,shaftwidth=0.02,headwidth=0.04,color=vec(0,0.5,1))       
        FLUX+=dot(dS,E)
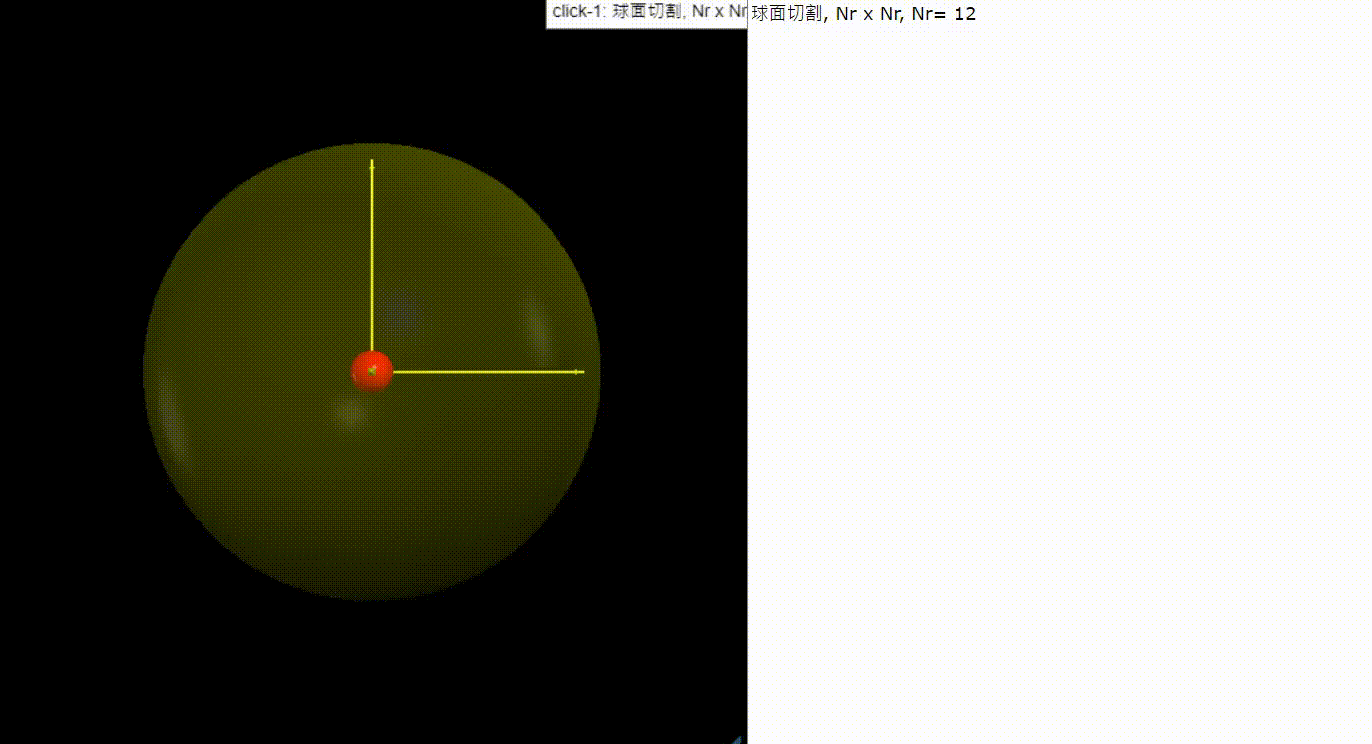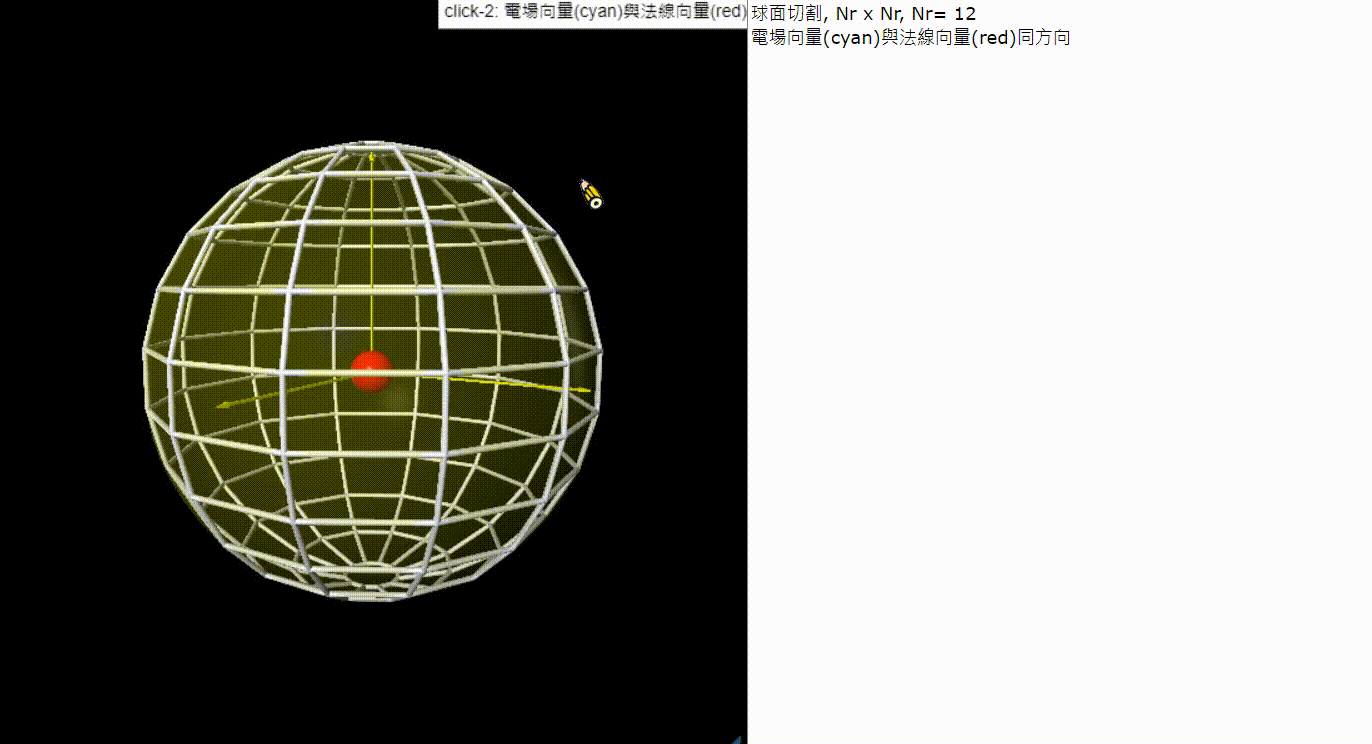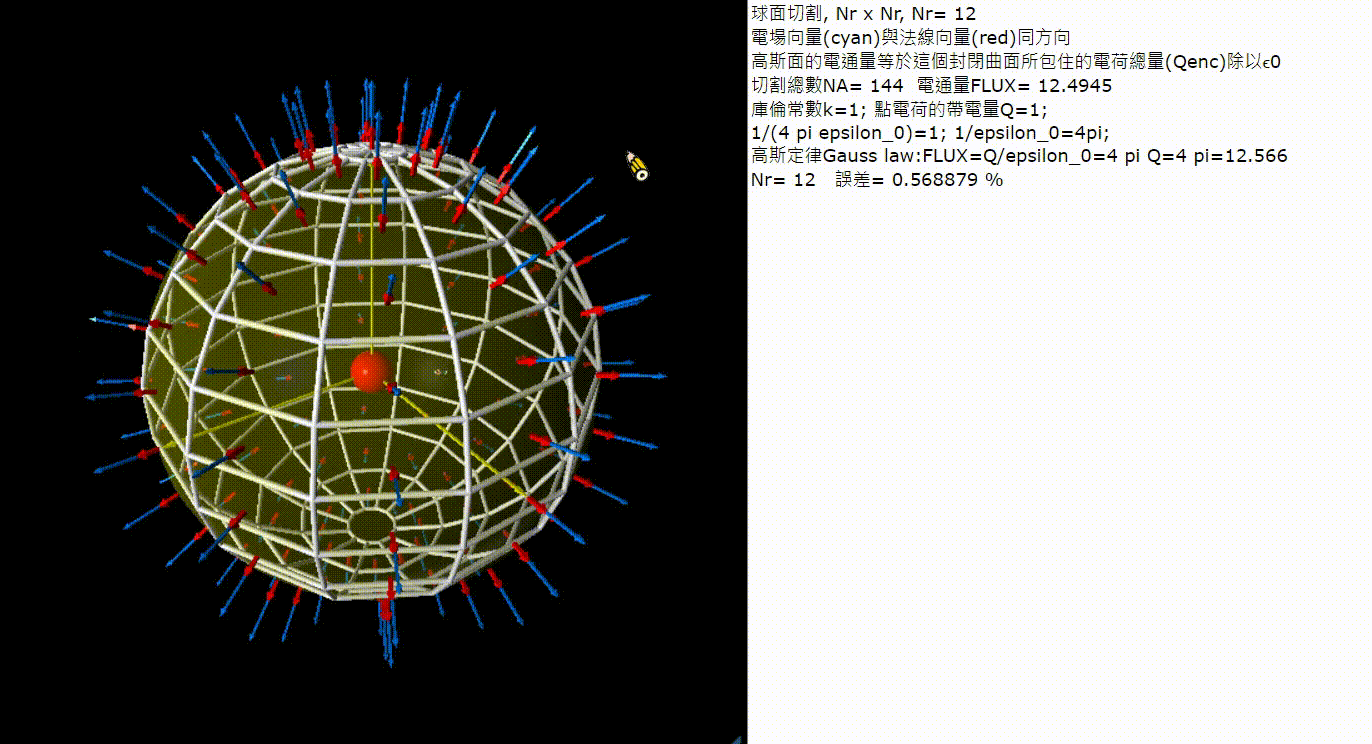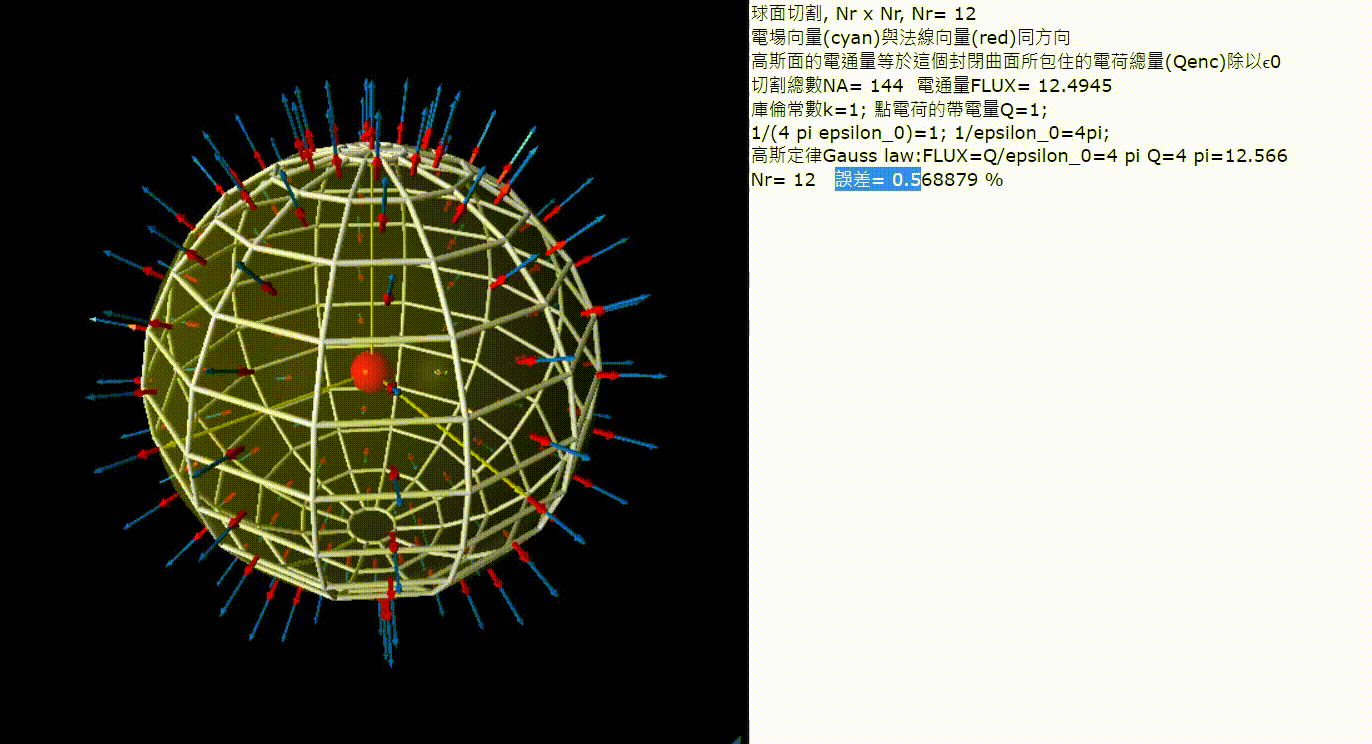
scene.pause('click-4:電通量')
LB.text='小曲面的電通量'
print('切割總數NA=',NA,' 電通量FLUX=',FLUX, '\nfor square plane:FLUX_1= 21.2637')    
# k=1; 1/(4 pi epsilon_0)=1; 1/epsilon_0=4pi; Gauss law:FLUX=Q/epsilon_0=4 pi Q=4 pi=12.566



    glowscript(PS-Gauss-02A.py)




  3. 點電荷在圓柱曲面的電通量

    4.
    在這個練習當中我們考慮點電荷的電場對一個圓柱曲面所產生的電通量，對於這個問題而言，我們當然要選擇圓柱坐標系統：\(\rho, \phi, z)\)，來處理繪圖和計算。計算的基本原理和前面兩個練習當中的做法是相同的。 
    Web VPython 3.2
def EF_point(q,rq,r):
    ke=1.
    rrq=r-rq
    rrq0=mag(rrq)
    Es=ke*q/rrq0**2
    E=ke*q*rrq/rrq0**3
    return E,Es
def plaq2(jz,jf):
    f=df*(jf-0.5); z=-H/2+dz*(jz-0.5)
    v1=vec(RG*cos(f),z,RG*sin(f))
    v2=vec(RG*cos(f),z+dz,RG*sin(f))
    v3=vec(RG*cos(f+df),z,RG*sin(f+df))
    v4=vec(RG*cos(f+df),z+dz,RG*sin(f+df))
    curve(pos=[v1,v2])
    curve(pos=[v1,v3])
    curve(pos=[v2,v4])
    curve(pos=[v3,v4])
    return

q1=10.; rq1=vec(0.,0.,0.); R=0.2; RG=2; H=4
scene=canvas(width=600, height=600, center=vector(0,0,0))
X=arrow(pos=vec(0,0,0),axis=vec(2,0,0),shaftwidth=0.02,\
   headwidth=0.04,color=vec(1,1,0))
Y=arrow(pos=vec(0,0,0),axis=vec(0,2,0),shaftwidth=0.02,\
   headwidth=0.04,color=vec(1,1,0))
Z=arrow(pos=vec(0,0,0),axis=vec(0,0,2),shaftwidth=0.02,\
   headwidth=0.04,color=vec(1,1,0))
plane1=box(pos=vec(0,0,2),size=vec(4,4,0.02),color=vec(0,1,1)\
   ,opacity=0.2)
Q1=sphere(pos=rq1,radius=R,color=vec(1,0,0))
print_options(width=400, height=600, readonly=False,digits=4\
   ,pos='right')
G=cylinder(pos=vec(0,-H/2,0),radius=RG,axis=vec(0,H,0)\
   ,color=vec(1,1,0), opacity=0.2)
Nf=16; Nz=8; NA=Nf*Nz; df=2*pi/Nf; dz=H/Nz; dA=RG*df*dz; 
NA=0; A=0; Aex=H*RG*pi/2; As=4*4; FLUX=0;
for jz in range(Nz):
    z=-H/2+dz*jz;
    for jf in range(Nf):
        if(jz in [4] and jf < 8): plaq2(jz,jf)
        if(jz in [1,2,3,4,5] and jf in [4]): plaq2(jz,jf)
        f=df*jf; 
        if(f >= pi*3/4): continue 
        if(f < pi*1/4): continue 
        NA+=1
        r1=vec(R*cos(f),0,R*sin(f))
        rG=vec(RG*cos(f),z,RG*sin(f))
        da=RG*df*dz
        A+=da
        dS=hat(r1)*da
        VN=arrow(pos=rG,axis=hat(r1)*0.5,shaftwidth=0.02,\
           headwidth=0.04,color=vec(1,0,0))
        E,Es=EF_point(q1,rq1,rG)
        VE=arrow(pos=rG,axis=E*0.2,shaftwidth=0.02,\
           headwidth=0.04,color=vec(0,0.5,1))
        FLUX+=dot(dS,E)
print(Nf,Nz,'切割總數NA=',NA,'\n面積比較:A,Aex,As=',A,Aex,As, \
    '\n圓柱曲面的電通量電通量FLUX=',FLUX,\
    '\n平面方塊的電通量=21.2637')



    glowscript(PS-Gauss-03A.py)




  4. 封閉的正方形曲面的高斯定律

    5.
    利用高斯定律我們可以快速的得到一個封閉曲面的電通量，高斯定律指出這個電通量的大小就是由曲面內的電荷總量所決定，把這個電荷總量除以\(\epsilon_0=1/(4\pi k)\)，就可以得到。在下面這個練習當中我們來驗證，如果有一個電荷存在於立方體所形成的封閉曲面內，那麼正方體6個面上的電通量總和就由這個電荷的電量所決定。 
    Web VPython 3.2
NL=4; L=4; L2=int(L/2); r=[];balls=[]; R1=0.1; R2=0.1; yc=L/2; D=3*L; ycc=3
cen=vec(0,yc,0)
scene=canvas(width=600, height=400, center=vec(0,2,0))
plane1=box(pos=cen,size=vec(L,0.1,L),color=vec(0,1,1))

cenp=sphere(pos=scene.center,radius=0.1,color=vec(1,1,1))
charge=sphere(pos=vec(0,0,0),radius=0.2,color=vec(0,1,0))
scene.forward=vec(-0.45, -0.31, -0.83)
print(scene.forward,scene.camera.pos)
for i in range(NL+1):
    a=arrow(pos=cen+vec(-L2,0.03,-L2+i),axis=vec(L,0,0),shaftwidth=0.05, \
    headwidth=0.05, color=vec(0.2,0.2,0.2))
    a=arrow(pos=cen+vec(-L2+i,0.03,-L2),axis=vec(0,0,L),shaftwidth=0.05, \
    headwidth=0.05, color=vec(0.2,0.2,0.2))
scene.pause('click-1')
eps0=1./(4*pi); E=[]; q=10
for i in range(NL):
    for j in range(NL):
        c0=vec(i-L2+0.5,L2,j-L2+0.5)
        v0=c0-charge.pos
        v0s=mag(v0)
        v1=q*hat(v0)/v0s**2
        ar=arrow(pos=c0,axis=v1,shaftwidth=0.1,headwidth=0.1,color=vec(1,0.5,0))
        sphere(pos=c0,radius=0.05,color=vec(1,0,0))
        E.append(ar)
FLUX=0; GAUSS=q/eps0
area=(L/NL)**2; n=vec(0,1,0)
for v in E:
    fx=dot(v.axis,n)*area
    FLUX+=fx
print('FLUX_1=',FLUX)
scene.pause('click-2')
cube=box(pos=vec(0,0,0),size=vec(L,L,L),color=vec(1,1,1),opacity=0.2)
print('According to symmetry, FLUX of box=6*FLUX_1=',FLUX*6)
print('k=1/(4*pi*eps0), 1/eps0=4*pi*k, Gauss law: q/eps0=4*pi*k*q=',GAUSS)



    glowscript(PS-Gauss-01.py)




  5. 封閉的圓球面的高斯定律

    6.
    延續上面一個練習，在這個問題當中我們來考慮封閉的球面包含了一個點電荷，這個封閉球面的電通量一樣是由內部所含的電荷的總量決定。 
    GlowScript 3.2 VPython
def EF_point(q,rq,r):
    ke=1.
    rrq=r-rq
    rrq0=mag(rrq)
    E=ke*q*rrq/rrq0**3
    return E    
q=79; rq=vec(0,0,0)
scene = canvas(width=1000, height=700, center=vec(0, 0, 0))
Xaxis=arrow(pos=vec(-4,0,0),axis=vec(8,0,0),shaftwidth=0.01, \ 
     headwidth=0.02)
Yaxis=arrow(pos=vec(0,-1,0),axis=vec(0,2,0),shaftwidth=0.01)
charge = sphere(pos=rq, radius=0.03, color=color.red)
Na=21; qa=2.; ma=4.; xa=-2; va=60; Ly=0.2; Ly2=Ly/2; dy=Ly/Na
qc=[qa for i in range(Na)]
es = [sphere(pos=vec(-2,-Ly2+dy*i,0), radius=0.03, \ 
   color=vec(0.5+0.5*random(),0.5+0.5*random(),0.5+0.5*random()), 
    make_trail=True) for i in range(Na)]
for i in range(Na):
    es[i].v=vec(va,0,0)
t=0.; dt=0.0002; NR=int(1/dt)
labva='va={:04.1f}'.format(va)
label(text=labva,pos=vector(-2,2,0))
print_options(width=1000, height=100)
print('q=',q,'  rq=',rq,'  Na=',Na,'  qa=',qa,'  ma=',ma, \
    '  xa=',xa,'  va=',va,'  Ly=',Ly)
scene.waitfor('click')
while t < 10:
    rate(NR/100)
    for i in range(Na):
        if(mag(es[i].pos) > 2.2): break
        E=EF_point(q,rq,es[i].pos)
        es[i].v+=qc[i]*E/ma*dt
        es[i].pos+=es[i].v*dt
    t+=dt



    glowscript(PS-Gauss-02.py)