克普勒(Kepler)行星運動定律
-
1. 行星繞日的軌道是橢圓形
2. 等面積定律:行星至太陽間的連心線在相同的時間內掃過相同的面積
3. 行星繞日的週期(T)與其橢圓軌道之半長軸(R)關係為: \(T^2 \propto a^3\)
半長軸a 近日點 遠日點 公週期 半徑 質量 自週期 衛星 軌傾角 離心率 脫離速 密度 3rdlaw AU AU AU year RE ME 24hr degree km/s g/cm3 T2/a3 太陽 --- --- --- --- 109 332,800 25-36 9 --- --- 617 1.41 水星 0.387 0.307 0.467 0.241 0.3824 0.055 58.65 0 7 0.206 4.3 5.43 1.002 金星 0.723 0.719 0.728 0.615 0.95 0.815 -243 0 3.39 0.007 10.4 5.25 1.000 地球 1 0.983 1.017 1 1 1 1 1 0 0.017 11.2 5.52 1.000 火星 1.523 1.381 1.666 1.88 0.53 0.107 1.026 2 1.85 0.093 5 3.94 1.000 木星 5.204 4.95 5.459 11.86 11.2 317.9 0.408 79 1.3 0.048 59.5 1.31 0.998 土星 9.582 9.041 10.12 29.46 9.46 95.2 0.425 82 2.49 0.056 35.6 0.69 0.986 天王星 19.20 18.32 20.08 84.01 4 14.52 -0.746 27 0.77 0.047 21.3 1.29 0.997 海王星 30.04 29.71 30.39 164.8 3.88 17.06 0.796 14 1.77 0.009 23.3 1.64 1.001 冥王星 39.48 29.65 49.30 247.7 0.18 0.0022 -6.37 5 17.15 0.248 1.1 2.03 0.997 哈雷 17.83 0.586 35.08 75.32 5.5km 2E14kg 2.2 0 162 0.967 2 m/s 0.6
半長軸a 近日點 遠日點 公週期 半徑 質量 自週期 衛星 軌傾角 離心率 脫離速 密度 3rdlaw
AU AU AU year RE ME 24hr degree km/s g/cm3 T2/a3
太陽 --- --- --- --- 109 332,800 25-36 9 --- --- 617 1.41
水星 0.387 0.307 0.467 0.241 0.3824 0.055 58.65 0 7 0.206 4.3 5.43 1.002
金星 0.723 0.719 0.728 0.615 0.95 0.815 -243 0 3.39 0.007 10.4 5.25 1.000
地球 1 0.983 1.017 1 1 1 1 1 0 0.017 11.2 5.52 1.000
火星 1.523 1.381 1.666 1.88 0.53 0.107 1.026 2 1.85 0.093 5 3.94 1.000
木星 5.204 4.95 5.459 11.86 11.2 317.9 0.408 79 1.3 0.048 59.5 1.31 0.998
土星 9.582 9.041 10.12 29.46 9.46 95.2 0.425 82 2.49 0.056 35.6 0.69 0.986
天王星 19.20 18.32 20.08 84.01 4 14.52 -0.746 27 0.77 0.047 21.3 1.29 0.997
海王星 30.04 29.71 30.39 164.8 3.88 17.06 0.796 14 1.77 0.009 23.3 1.64 1.001
冥王星 39.48 29.65 49.30 247.7 0.18 0.0022 -6.37 5 17.15 0.248 1.1 2.03 0.997
哈雷 17.83 0.586 35.08 75.32 5.5km 2E14kg 2.2 0 162 0.967 2 m/s 0.6
============================================================================
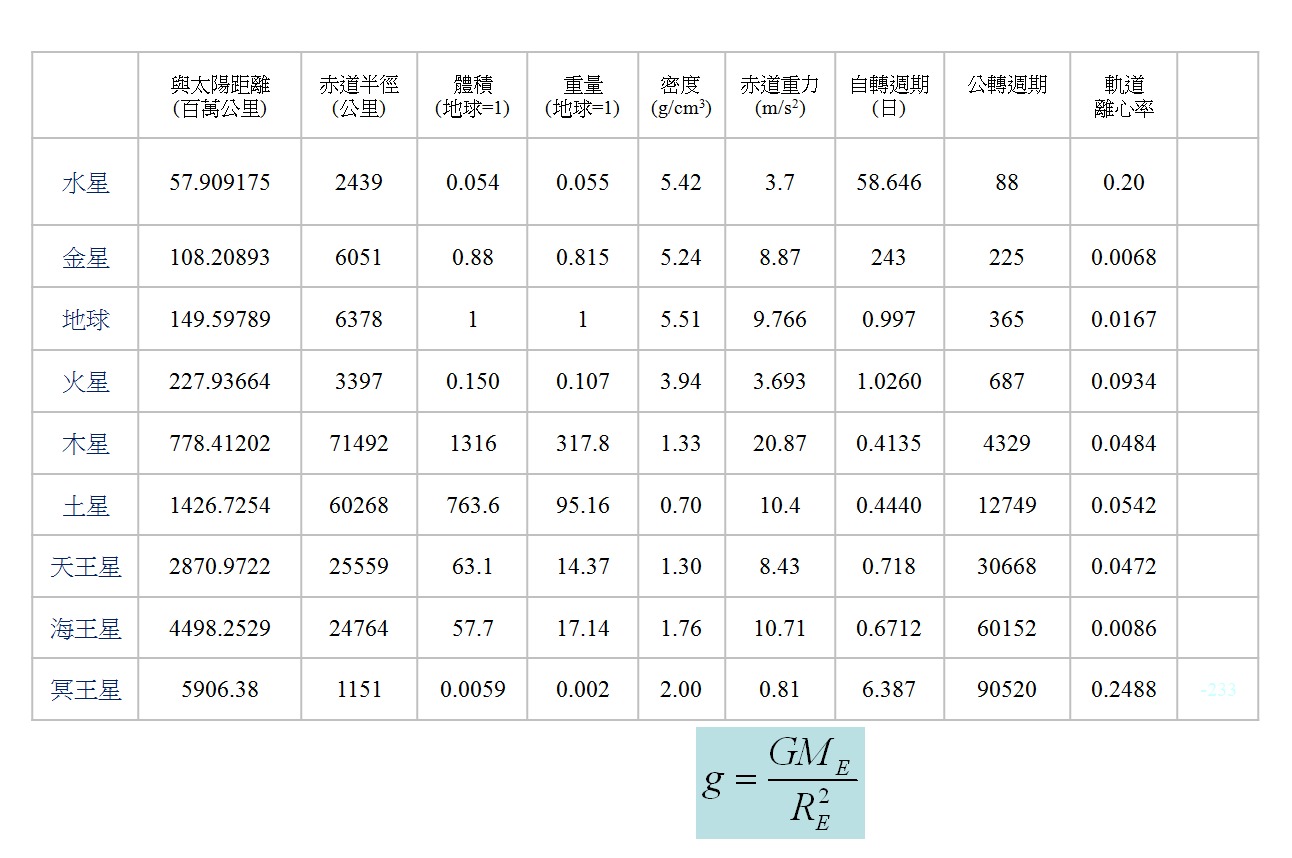
太陽距離 半徑 體積 重量 密度 赤道 自轉週 公轉 軌道 表面 自轉 衛星 最亮星等 最大視
Mkm 公里 地球1 地球1 g/cm3 重力 期(日) 週期 離心率 溫度(C) 方向 最亮星等 直徑
水星 57.9 2439.7 0.054 0.055 5.427 3.7 58.646 87.97日 0.2056 -173~427 西東 0 -1.9等 11秒
金星 108.2 6051.8 0.88 0.815 5.24 8.87 243 224.7日 0.0068 420~485 東西 0 -4.4等 61秒
地球 149.6 6378.1 1 1 5.515 9.766 0.99726 365.2日 0.0167 -88~58 西東 1 - -
火星 227.9 3397.0 0.15 0.10744 3.94 3.693 1.026 686.9日 0.0934 -87~-5 西東 2 -2.8等 18秒
木星 778.4 71492.0 1316 317.82 1.33 20.87 0.41354 11.85年 0.04839 -148 西東 63 -2.8等 47秒
土星 1426.7 60268.0 763.6 95.16 0.7 10.4 0.44401 29.44年 0.05415 -178 西東 56 +0.4等 43秒(環)
天王星 2871.0 25559.0 63.1 14.371 1.3 8.43 0.718 84.02年 0.04716 -216 西東 27 5.6等 4秒
海王星 4498.3 24764.0 57.7 17.147 1.76 10.71 0.67125 164.7年 0.00859 -214 西東 13 7.9等 0秒
冥王星 5906.4 1151.0 0.0059 0.0022 2 0.81 6.387 247.9年 0.2488 -233 西東 3 13.7等 0秒
行星運動方程式與重力定律
行星運動的動力是牛頓的重力定律,而運動的法則是牛頓第二運動定律:
運動的差分近似如下
什麼樣的條件是形成圓週運動的恰好條件呢?非常簡單,在圓週運動當中的向心力剛好就是這個行星與太陽之間的重力,這個行星的運動將會遵循圓週運動 ,因此圓週運動的恰好條件如下: \[f_c=\frac{4 \pi^2 m r}{T^2}=f_g=\frac{G M_s m}{r^2} \] \(M_s=太陽的質量\)。將等式兩邊的行星質量\(m\)消去,再做一些代數化簡就可以得到下面這個週期與距離的關係式:
 \[\frac{1^3}{1^2}=\frac{GM_s}{4\pi^2}, \,\,\, GM_s=4\pi^2\]
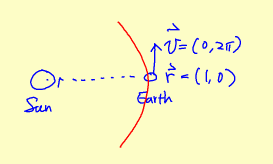
因此在這個單位系統中\(GM_s=4\pi^2\),地球在某一個時刻的坐標為\(\vec{r}=(1,0)\),而這個時刻的速度為\(\vec{v}=(0,2\pi) \,\, v=\frac{2\pi r}{T}=\frac{2\pi \cdot 1}{1}=2\pi\)。
\[\frac{1^3}{1^2}=\frac{GM_s}{4\pi^2}, \,\,\, GM_s=4\pi^2\]
因此在這個單位系統中\(GM_s=4\pi^2\),地球在某一個時刻的坐標為\(\vec{r}=(1,0)\),而這個時刻的速度為\(\vec{v}=(0,2\pi) \,\, v=\frac{2\pi r}{T}=\frac{2\pi \cdot 1}{1}=2\pi\)。在下面的程式中我們就體現了這個單位系統,先將它運用在地球繞日的軌道運動中。依據上述的單位系統地球繞日的週期為1,地球與太陽的距離也是1,軌道將是圓。
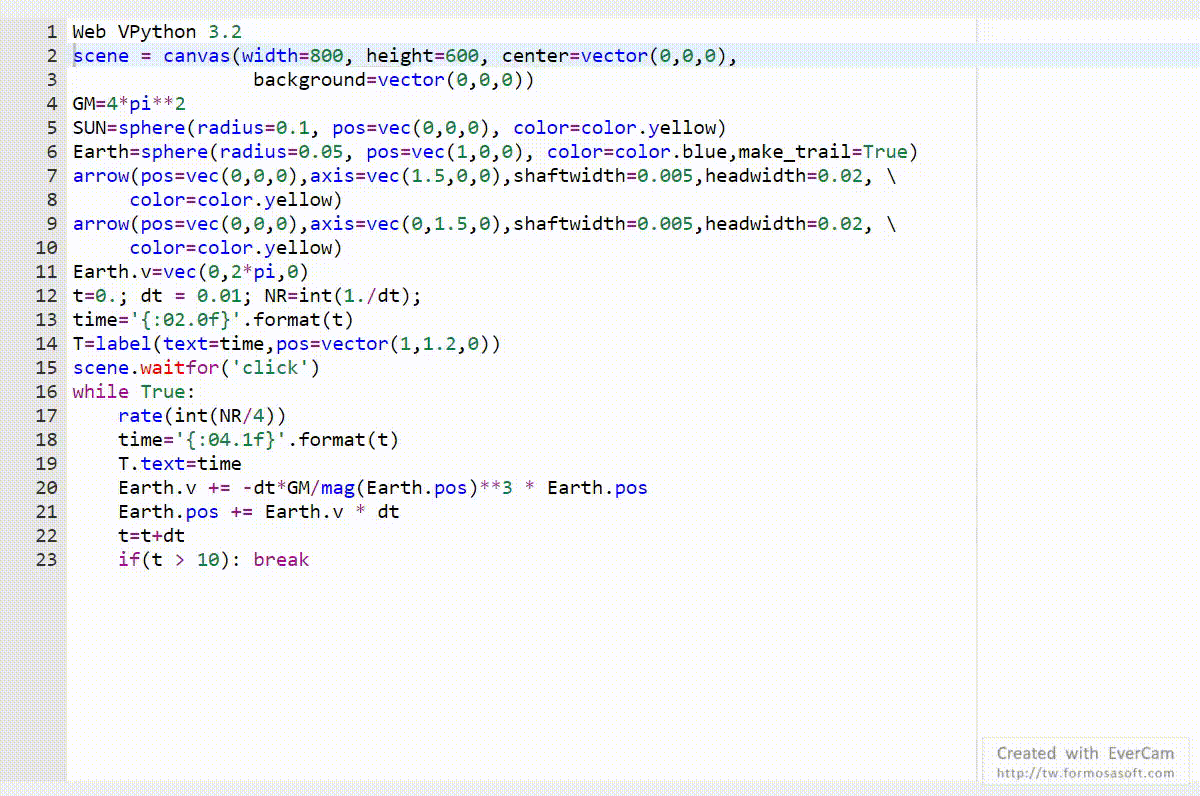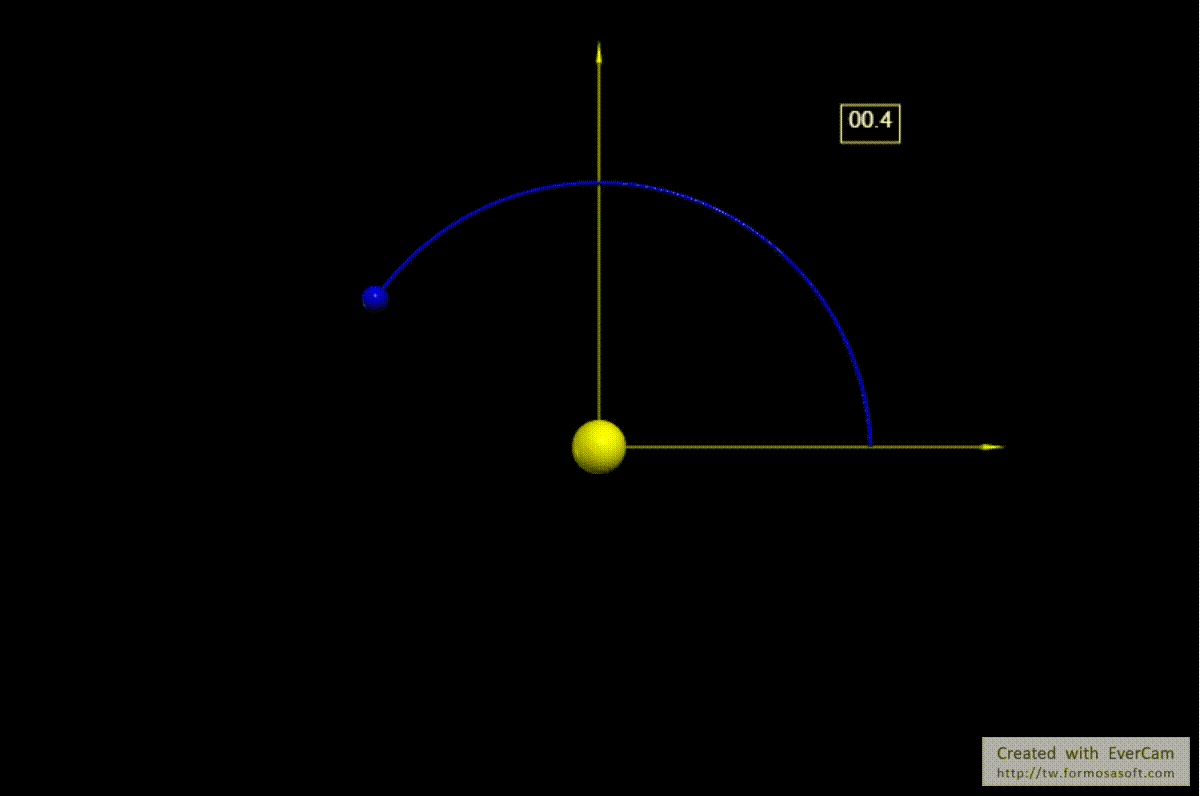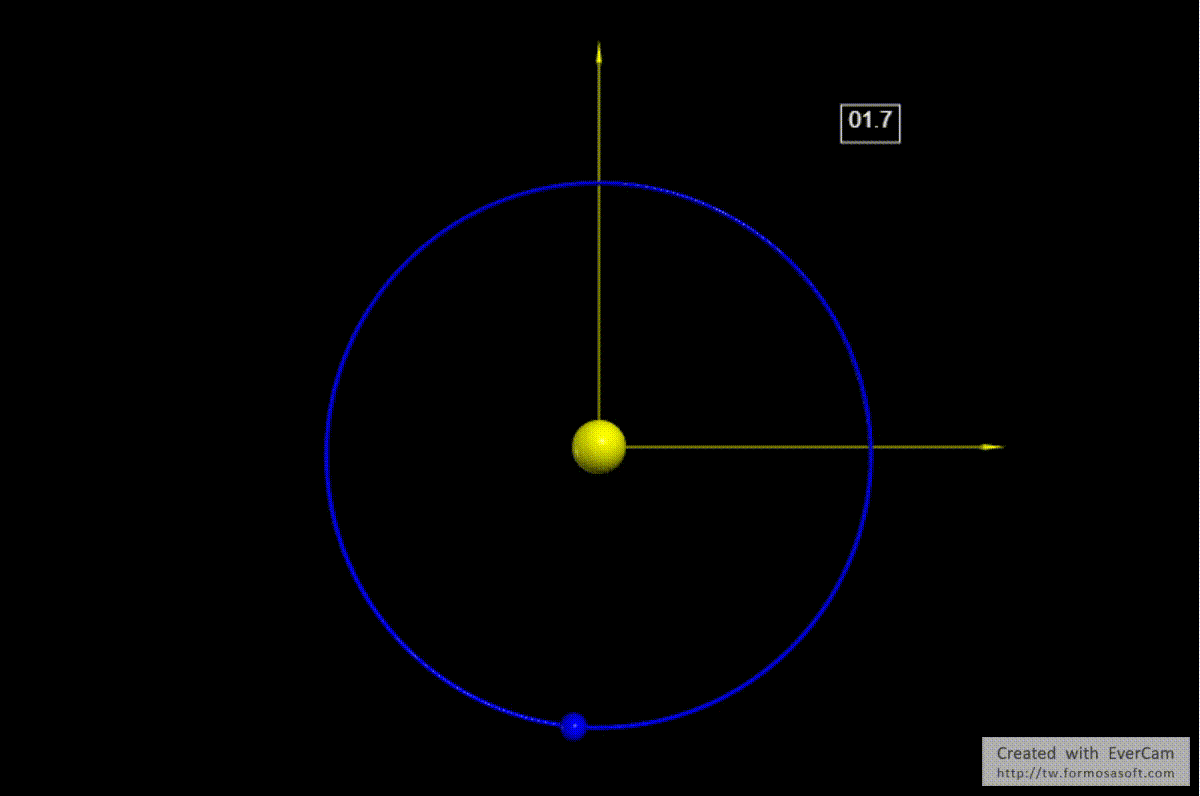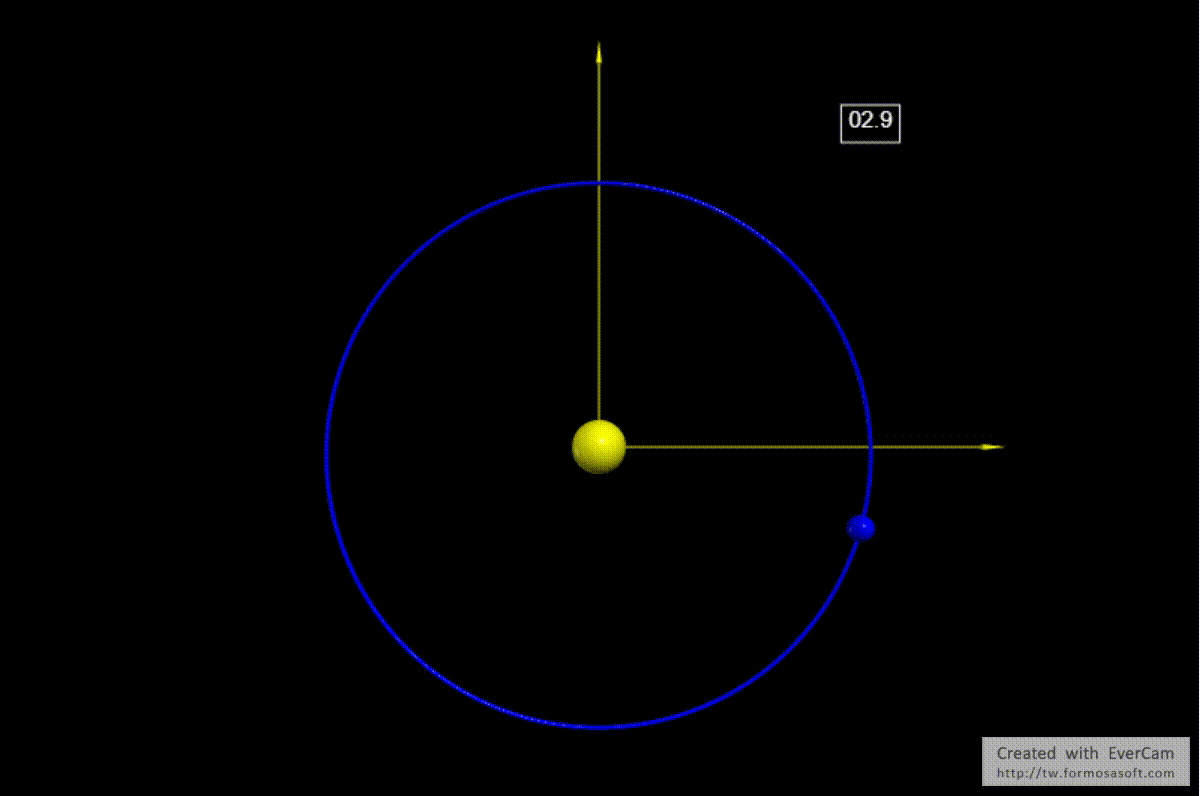
Web VPython 3.2
scene = canvas(width=800, height=600, center=vector(0,0,0),
background=vector(0,0,0))
GM=4*pi**2
SUN=sphere(radius=0.1, pos=vec(0,0,0), color=color.yellow)
Earth=sphere(radius=0.05, pos=vec(1,0,0), color=color.blue,make_trail=True)
arrow(pos=vec(0,0,0),axis=vec(1.5,0,0),shaftwidth=0.005,headwidth=0.02, \
color=color.yellow)
arrow(pos=vec(0,0,0),axis=vec(0,1.5,0),shaftwidth=0.005,headwidth=0.02, \
color=color.yellow)
Earth.v=vec(0,2*pi,0)
t=0.; dt = 0.01; NR=int(1./dt);
time='{:02.0f}'.format(t)
T=label(text=time,pos=vector(1,1.2,0))
scene.waitfor('click')
while True:
rate(int(NR/4))
time='{:04.1f}'.format(t)
T.text=time
Earth.v += -dt*GM/mag(Earth.pos)**3 * Earth.pos
Earth.pos += Earth.v * dt
t=t+dt
if(t > 10): break
|
 |
行星繞日的軌道是橢圓形
Web VPython 3.2
orb=['mercury','venus','earth','mars']
ra=[0.467,0.728,1.017,1.666]
rp=[0.307,0.719,0.983,1.381]
NP=len(ra)
GMs=4*pi**2; dt=0.0001; NR=int(1/dt)/4; V=[] #pi=math.pi
for i in range(NP):
ai=(ra[i]+rp[i])/2.
rat=rp[i]/ra[i]/((rp[i]+ra[i])/2.)
vir=rat**0.5
V.append(vir*2*pi)
ei=abs(1-((vir*2*pi)**2*(ra[i])/4/pi**2))
Ti=ai**1.5
PL='{:4d}'.format(i)+' {:10s}'.format(orb[i])+'{:9.3f}'.format(ra[i]) \
+'{:9.3f}'.format(rp[i])+'{:9.3f}'.format(ai)+'{:9.3f}'.format(vir) \
+'{:9.3f}'.format(V[i])+'{:9.3f}'.format(ei)+'{:9.3f}'.format(Ti)
print(PL)
scene=canvas(width=800, height=700, center=vector(0,0,0),
background=vector(0,0,0))
SUN = sphere(radius=0.1,pos=vector(0,0,0),color=color.yellow)
planets=[sphere(radius=0.2, pos=vector(ra[i],0,0), make_trail=True) \
for i in range(NP)]
planets[0].radius=0.03; planets[0].color=vec(0.5,0.5,0.5)
planets[1].radius=0.05; planets[1].color=vec(0.8,0.8,0.8)
planets[2].radius=0.1; planets[2].color=color.cyan
planets[3].radius=0.05; planets[3].color=color.orange
for i in range(NP):
planets[i].trail_color=planets[i].color
planets[i].v=vector(0,V[i],0)
t=0.
time='{:4.1f}'.format(t)
T=label(text=time,pos=vector(1.5,1.5,0))
scene.waitfor('click')
while True:
rate(NR)
time='{:4.1f}'.format(t)
T.text=time
for i in range(NP):
a=-GMs/mag(planets[i].pos)**3 * planets[i].pos
planets[i].v += a*dt
planets[i].pos += planets[i].v * dt
t=t+dt
if(t > 8): break
|
 |
哈雷彗星的軌道
 |
GlowScript 3.0 VPython
orb=['mercury','venus','earth','mars','jupiter','saturn','uranus','neptune','pluto','halley']
ra=[0.467,0.728,1.017,1.666,5.459,10.124,20.078,30.386,49.304,35.082]
rp=[0.307,0.719,0.983,1.381,4.95,9.041,18.324,29.709,29.658,0.586]
a=[0.387,0.724,1,1.523,5.204,9.582,19.201,30.047,39.481,17.834]
va=[1.303,1.168,0.983,0.738,0.417,0.305,0.218,0.18,0.123,0.031]
e=[0.207,0.006,0.017,0.094,0.049,0.057,0.046,0.011,0.249,0.967]
T=[0.241,0.615,1,1.88,11.86,29.46,84.01,164.8,247.7,75.32]
NP=len(rp)-2; NP=10
RE=1.5e11; TE=365*86400; VE=2.*pi*RE/TE
MS=1.989e30; ME=5.972e24; G=6.67e-11; V=[]
Ns=1000; dt = TE/Ns; NR=Ns*2
print(' i planets ra rp a va e T')
for i in range(NP):
ai=(ra[i]+rp[i])/2.
rat=rp[i]/ra[i]/((rp[i]+ra[i])/2.)
vir=sqrt(rat)
ei=abs(1-((vir*2*pi)**2*(ra[i])/4/pi**2))
PL='{:4d}'.format(i)+'{:10s}'.format(orb[i])+'{:9.3f}'.format(ra[i]) \
+'{:9.3f}'.format(rp[i])+'{:9.3f}'.format(ai)+'{:9.3f}'.format(vir) \
+'{:9.3f}'.format(ei)+'{:9.3f}'.format(T[i])
print(PL)
vi=VE*vir
V.append(vi)
ran=random
scene = canvas(width=800, height=700, center=vector(0,0,0),
background=vector(0,0,0))
SUN = sphere(radius=0.1*RE,pos=vector(0,0,0),color=color.yellow)
planets=[sphere(radius=0.2*RE, pos=vector(ra[i]*RE,0,0), make_trail=True) for i in range(NP)]
planets[0].radius=0.02*RE
planets[1].radius=0.05*RE
planets[2].radius=0.1*RE
planets[3].radius=0.05*RE
planets[4].radius=0.3*RE
planets[0].color=color.cyan
planets[1].color=color.orange
planets[2].color=color.blue
planets[3].color=color.red
planets[4].color=color.orange
planets[5].color=color.green
planets[6].color=color.white
planets[7].color=color.purple
planets[8].color=color.white
planets[9].color=color.yellow
for i in range(NP):
planets[i].trail_color=planets[i].color
planets[i].v=vector(0,V[i],0)
t=0.
time='{:4.0f}'.format(t/TE)
T=label(text=time,pos=vector(40*RE,10*RE,0))
scene.waitfor('click')
while True:
rate(NR)
time='{:4.0f}'.format(t/TE)
T.text=time
for i in range(2,NP):
planets[i].v += -dt*G*MS/mag(planets[i].pos)**3 * planets[i].pos
planets[i].pos += planets[i].v * dt
t=t+dt
if(t/TE > 80): break
等面積定律
 |