拋體運動

1. 拋體運動之精確解
當我們考慮自由落體運動的時候，物體所受到的重力與其初速度的方向相同，因此後續的運動維持在同一個線上，是一個一維運動。如果物體的初始速度與重力的方向不同，運動的形態將會成為一個二維的運動，因此我們把所有的物理量都寫成兩個分量的向量形式如下： \[a_x = 0\] \[a_y = g\] \[v_x(t)=v_0 \cos(\theta) t\] \[v_y(t)=v_0 \sin(\theta) t - g t\] \[ x(t)=v_0 \cos(\theta) t, \] \[ y(t)=v_0 \sin(\theta) t-\frac{1}{2} g t^2 \] 可以看得出來物體的運動方式，就是x方向的等速度運動與y方向的等加速度運動的合成，運動的軌跡就是一個拋物線方程式所描述的軌跡。因為已經可以精確的推導出物體的位置向量隨著時間變化的函數關係。我們可以直接將這兩個方程式\( x(t)=v_0 \cos(\theta) t; \,\,\,\, y(t)=v_0 \sin(\theta) t-\frac{1}{2} g t^2 \)放進vpython的程式當中，直接進行拋體運動的物理模擬。依此想法所完成的程式如下：

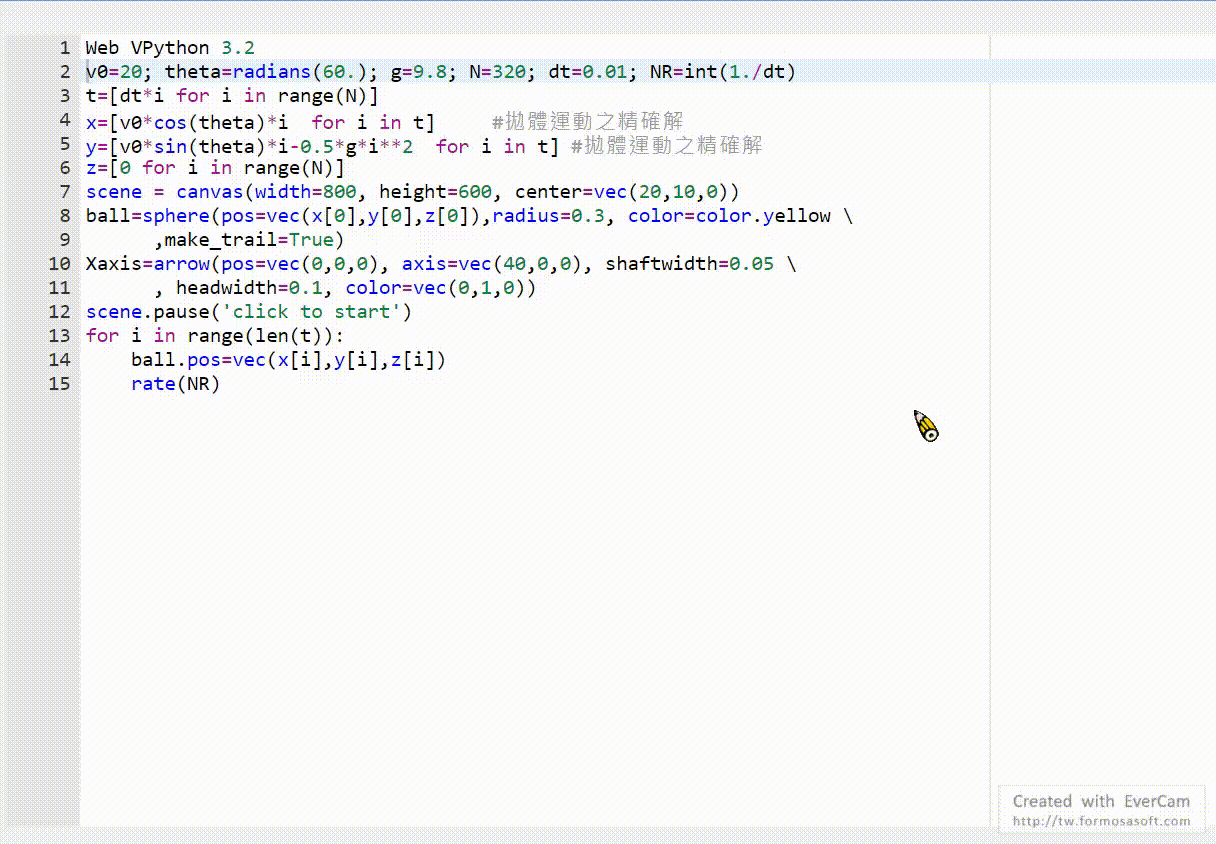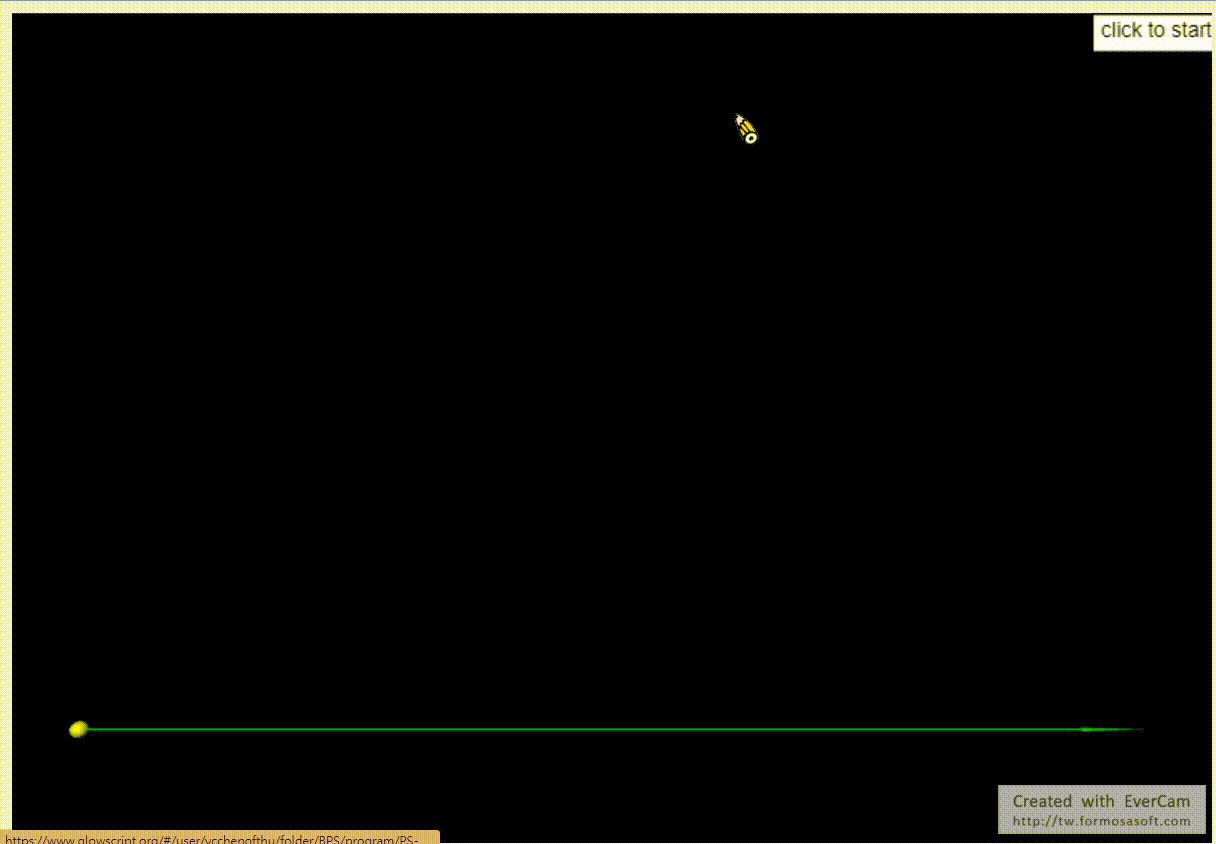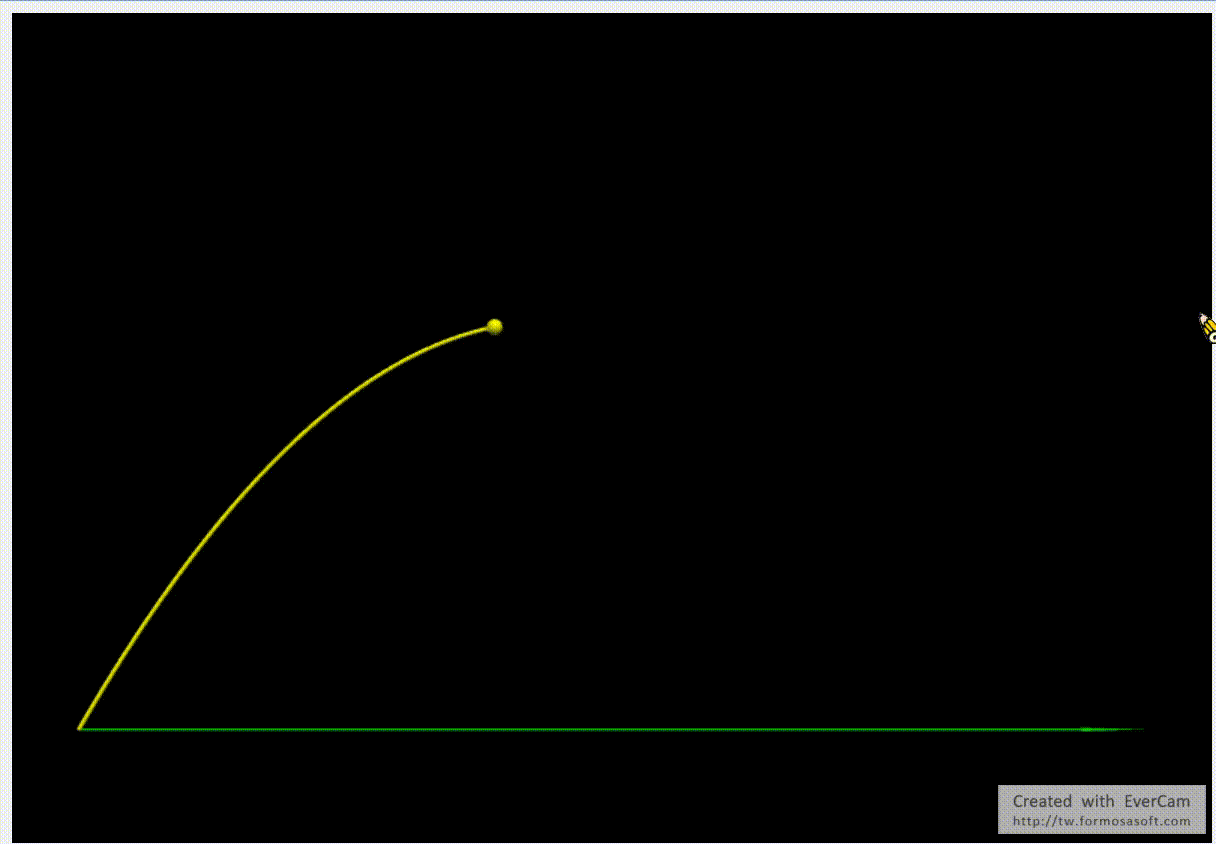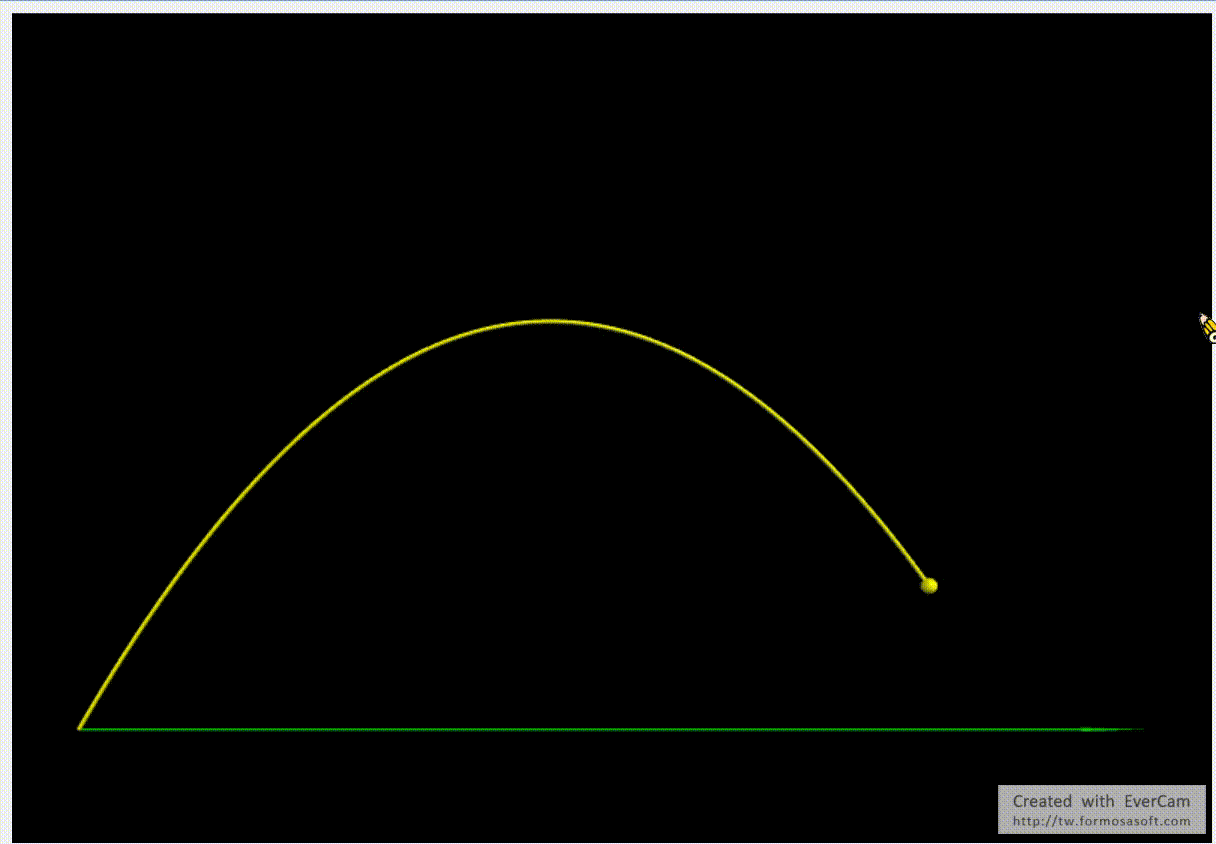
Web VPython 3.2 v0=20; theta=radians(60.); g=9.8; N=320; dt=0.01; NR=int(1./dt) t=[dt*i for i in range(N)] x=[v0*cos(theta)*i for i in t] #拋體運動之精確解 y=[v0*sin(theta)*i-0.5*g*i**2 for i in t] #拋體運動之精確解 z=[0 for i in range(N)] scene = canvas(width=800, height=600, center=vec(20,10,0)) ball=sphere(pos=vec(x[0],y[0],z[0]),radius=0.3, color=color.yellow \ ,make_trail=True) Xaxis=arrow(pos=vec(0,0,0), axis=vec(40,0,0), shaftwidth=0.05 \ , headwidth=0.1, color=vec(0,1,0)) scene.pause('click to start') for i in range(len(t)): ball.pos=vec(x[i],y[i],z[i]) rate(NR)



glowscript(PS-projectile-1.py)





---



2. 拋體運動數值模擬(差分近似)

三維運動方程式的差分近似:

\[ \vec{v}(t+dt)=\vec{v}(t)+\vec{a}dt \] \[ \vec{r}(t+dt)=\vec{r}(t)+\vec{v}dt \] 物體在三維空間中運動的時候，它所受到的力量是一個向量，所以加速度向量，速度向量和位置向量的更新都必須考慮三個分量。也就是這樣的差分方程式總共有下列6個： \[ v_x(t+dt)=v_x(t)+ a_x dt \] \[ v_y(t+dt)=v_y(t)+ a_y dt \] \[ v_z(t+dt)=v_z(t)+ a_z dt \] \[ x(t+dt)=x(t)+ v_x dt \] \[ y(t+dt)=y(t)+ v_y dt \] \[ z(t+dt)=z(t)+ v_z dt \]

對於拋體運動而言，它是一個二維的運動所以只有4個差分方程。 拋體運動只受到重力往下作用所以x方向的加速度為0，\(a_x=0\)。也就是在x方向位置隨時間的變化是線性關係的等速度運動。所以在整個程式的設計當中只用到下面3個差分方程：
\[ x(t+dt)=x(t)+ v_x dt \] \[ v_y(t+dt)=v_y(t) - 9.8 dt \] \[ y(t+dt)=y(t)+ v_y dt \]

Web VPython 3.2 Web VPython 3.2 v0=20; theta=radians(60.); g=9.8; gv=vec(0,-g,0); N=600; tm=0; dt=0.02; NR=int(1./dt) t=[dt*i for i in range(N)] x=[v0*cos(theta)*i for i in t] #拋體運動之精確解 y=[v0*sin(theta)*i-0.5*g*i**2 for i in t] #拋體運動之精確解 z=[0 for i in range(N)] scene = canvas(width=800, height=600, center=vec(20,10,0)) ball1=sphere(pos=vec(x[0],y[0],z[0]),radius=0.3, color=color.yellow \ ,make_trail=True) Xaxis=arrow(pos=vec(0,0,0), axis=vec(40,0,0), shaftwidth=0.05 \ , headwidth=0.1, color=vec(0,1,0)) ball2=sphere(pos=vec(x[0],y[0],z[0]),radius=0.3, color=color.cyan \ ,make_trail=True, opacity=0.5) ball2.v=vec(v0*cos(theta),v0*sin(theta),0) scene.pause('click to start') i=0 while tm < 10: rate(NR) ball1.pos=vec(x[i],y[i],z[i]) ball2.v+=gv*dt #拋體運動之差分近似 ball2.pos+=ball2.v*dt #拋體運動之差分近似 if(ball2.pos.y < 0): break tm+=dt; i+=1



glowscript(PS-projectile-2.py)





---



3. 拋體運動加入空氣阻力
假設阻力的大小可以表示為下面的公式: \(\vec{f}_r=-mC\vec{v}\), \(m\)=落體質量，\(C\)=阻力係數, \(\vec{v}\)=速度向量。請注意到阻力的方向總是與物體運動的方向相反，所以他會削減掉速度的大小，動能就會損失。
\[\vec{f}=\vec{f}_g+\vec{f}_r=m\vec{g}-mC\vec{v} \] \[\vec{a}=\frac{\vec{f}}{m}=\vec{g}-C\vec{v} \] \[\frac{d\vec{v}}{dt}=\vec{g}-C\vec{v} \]



Web VPython 3.2 v0=20; theta=radians(60.); g=9.8; gv=vec(0,-g,0); N=600; C=0.3 t=0; dt=0.02; NR=int(1./dt) scene = canvas(width=800, height=600, center=vec(20,10,0)) Xaxis=arrow(pos=vec(0,0,0), axis=vec(40,0,0), shaftwidth=0.05 \ , headwidth=0.1, color=vec(0,1,0)) ball1=sphere(pos=vec(0,0,0),radius=0.3, color=color.yellow \ ,make_trail=True) ball1.v=vec(v0*cos(theta),v0*sin(theta),0) ball2=sphere(pos=vec(0,0,0),radius=0.3, color=color.cyan \ ,make_trail=True, opacity=0.5) ball2.v=vec(v0*cos(theta),v0*sin(theta),0) scene.pause('click to start') i=0 while t < 10: rate(NR) ball1.v+=gv*dt ball1.pos+=ball1.v*dt ball2.v+=(gv-C*ball2.v)*dt ball2.pos+=ball2.v*dt if(ball2.pos.y < 0): break t+=dt



glowscript(PS-projectile-3.py)





---