GP1-L06
the distance=______m
01: ANS:=36
Solution:
\(a=\dfrac{f_{s,max}}{m}=\mu_s g=(0.25)(9.8m/s^2)=2.45m/s^2\)
\(|\Delta x|=\dfrac{v^2}{2a}=\dfrac{(13.3m/s)^2}{2(2.45m/s^2)}=36m\)
\(\mu_k\)=______
02: ANS:=0.6
Solution:
\(a=\dfrac{v^2}{2\Delta x}=\dfrac{(1.75m/s)^2}{2(1.2m)}=1.28m/s^2\)
\(F-\mu_k mg=ma\)
\(\mu_k=\dfrac{F-ma}{mg}=\dfrac{25N-(3.5kg)(1.28m/s^2)}{(3.5kg)(9.8m/s^2)}=0.6\)
A \(2.5\) kg block is initially at rest on a horizontal surface. A horizontal force \(\vec{F}\) of magnitude \(6\) N and a vertical force are \(\vec{P}\) are then applied to the block (in the Fig). The coefficients of friction for the block and surface are \(\mu_s=0.4\) and \(\mu_k=0.25\) . Determine the magnitude of the frictional force acting on the block if the magnitude of \(\vec{P}\) is (a) 8N, (b) 10N, and (c) 12N. (03小題)
(a)f=______N
03: ANS:=6
(b)f=______N
04: ANS:=3.6
(c)f=______N
05: ANS:=3.1
Solution:
\(F_N=mg-P\)
\(f_{s,max}=\mu_s F_N\)
(a)\(P=8N\)
\(F_N=mg-P=(2.5)(9.8)-8=16.5N\)
\(f_{s,max}=\mu_s F_N=(0.4)(16.5)=6.6N \gt 6N\)
\(f=F=6N\)
(b)\(P=10N\)
\(F_N=mg-P=(2.5)(9.8)-10=14.5N\)
\(f_{s,max}=\mu_s F_N=(0.4)(14.5)=5.8N\)
最大淨摩擦\(f_{s,max}=5.8N\)小於\(F=6N\)，因此積木開始移動
\(f_k=\mu_k F_N=(0.4)(14.5)=3.6N\)
(c)\(P=12N\)
\(F_N=mg-P=(2.5)(9.8)-12=12.5\)
\(f_{s,max}=\mu_s F_N=(0.4)(12.5)=5N\)
最大淨摩擦\(f_{s,max}=5.8N\)小於\(F=6N\)，因此積木已經移動
\(f_k=\mu_k F_N=(0.25)(12.5)=3.1N\)
\(\mu_k\)=______
06: ANS:=0.6
Solution:
\(\mu_k=\dfrac{f}{mg}=\dfrac{485N}{(83kg)(9.8m/s^2)}=0.6\)
A \(12 \) N horizontal force \(\vec{F}\) pushes a block weighing 5 N against a vertical wall ( see the figure). The coefficient of static friction between the wall and the block is 0.6, and the coefficient of kinetic friction is 0.4. Assume that the block is not moving initially. (a) Will the block move? (b) In unit-vector notation, what is the force on the block from the wall? (03小題)
(a)yes=1, no=2
07: ANS:=2
(b)\(\vec{F}=a\hat{i}+b\hat{j}\), a=______
08: ANS:=-12
b=______
09: ANS:=5
Solution:
\(f_{s,max}=\mu_s F_N=(0.6)(12)=7.2N \lt 5N\)，積木不會移動
(b)\(\vec{F}_{wall}=-F_N\hat{i}+f\hat{j}=-12\hat{i}+5\hat{j}\)
In the figure, a box of Cheerios (mass \(m_C=1 \) kg ) and a box of Wheaties (mass \(m_W=3 \) kg ) are accelerated across a horizontal surface by a horizontal force \(\vec{F}\) applied to the Cheerios box. The magnitude of the frictional force on the Cheerios box is \(2.0 \) N, and the magnitude of the frictional force on the Wheaties box is \(3.5 N\). If the magnitude of \(\vec{F}\) is \(12\) N, what is the magnitude of the force on the Wheaties box from the Cheerios box? (01小題)
F'=______N
10: ANS:=8.3
Solution:
\(f_{total}=2N+3.5N=5.5N\)
\(F-f=ma\)
\(a=\dfrac{12N-5.5N}{1kg+3kg}=1.6m/s^2\)
\(F'-f_W=m_W a\)
\(F'=m_W a+f_W=(3kg)(1.6m/s^2)+3.5N=8.3N\)
When the three blocks in the figure are released from rest, they accelerate with a magnitude of \(0.5\) m/s2. Block 1 has mass M, block 2 has 2M, and block 3 has 2M. What is the coefficient of kinetic friction between block 2 and the table? (01小題)
\(\mu_k\)=______
11: ANS:=0.372
Solution:
\(2Mg-\mu_k(2Mg)-Mg=(M+2M+2M)(0.5 m/s^2)\)
\(\mu_k=\dfrac{M(9.8-2.5)}{2M(9.8)}=0.372\)
Block B in the figure weighs \(711 N\). The coefficient of static friction between block and table is 0.25; angle \(\theta\) is \(30^0\); assume that the cord between B and the knot is horizontal. Find the maximum weight of block A for which the system will be stationary. 圖中木塊B重711N。木塊與桌面的靜摩擦係數為0.25。角度為30度。假設木塊B與繩結之間的繩子是水平的。問系統靜止條件下木塊A的最大重量為何？ (01小題)
the maximum weight of block A=______N
12: ANS:=103
Solution:
\(T_2 \cos\theta-T_1=0\)
\(W_A=T_2 \sin\theta=\dfrac{T_1}{\cos\theta} \sin\theta=\mu_k W_B \dfrac{\sin\theta}{\cos\theta}\)
\(W_A=(0.25)(711)(\dfrac{\sin30^0}{\cos30^0})=103\) N
Body A in the figure weighs \(102\),N and body B weighs \(32\) N. The coefficients of friction between A and the incline are \(\mu_s=0.56\) and \(\mu_k=0.25\) . Angle \(\theta\) is 40°. Let the positive direction of an x axis be up the incline. In unit-vector notation, what is the acceleration of A if A is initially (a) at rest, (b) moving up the incline, and (c) moving down the incline? (03小題)
(a)a=______\(m/s^2\)
13: ANS:=0
(b)a=______\(m/s^2\)
14: ANS:=-3.9
(c)a=______\(m/s^2\)
15: ANS:=-1
Solution:
(a)A靜止，所以\(a=0\)(b)\(T-f_k-W_A \sin \theta=m_A a\)
\(f_k=\mu_k F_N\)
\(f_k=\mu_k F_N\)
\(F_N=W_A \cos \theta\)
\(W_B-T=m_B a\)
\(a=\dfrac{W_B-W_A \sin\theta-\mu_k W_A \cos\theta}{m_B+m_A}=\dfrac{32-102 \sin40^0-0.25 (102)-\cos 40^0}{\dfrac{32+102}{9.8}}=-3.9\)
(c)\(T+f_k-W_A \sin\theta=m_A a\)
\(a=\dfrac{W_B-W_A \sin \theta +\mu_k W_A \cos \theta}{m_B+m_A}=\dfrac{32-102 \sin40^0+0.25(102)\cos 40^0}{\dfrac{32+102}{9.8}}=-1\)
R=______m
16: ANS:=20.7
Solution:
摩擦力\(f_{s,max}=\mu_s F_N=\mu_s m g\)
向心力\(f=\dfrac{mv^2}{R}\)
\(f \le f_{s,max}\)
\(\dfrac{mv^2}{R} \le \mu_s m g\)
\(R \ge \dfrac{v^2}{\mu_s g}=\dfrac{(8.06m/s)^2}{(0.32)(9.8m/s^2)}=20.7m\)
nprob= 11 11
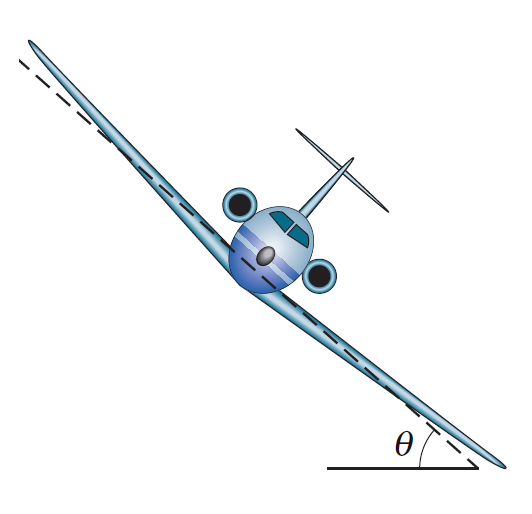An airplane is flying in a horizontal circle at a speed of v (figure). If its wings are tilted at angle \(\theta\)(=theta) to the horizontal, what is the radius of the circle in which the plane is flying? Assume that the required force is provided entirely by an “aerodynamic lift” that is perpendicular to the wing surface. (01小題)
the radius of the circle \(r\)=_____ [g,v,theta]
17: ANS:=v**2/(g*tan(theta))
Solution:
nprob= 12 12
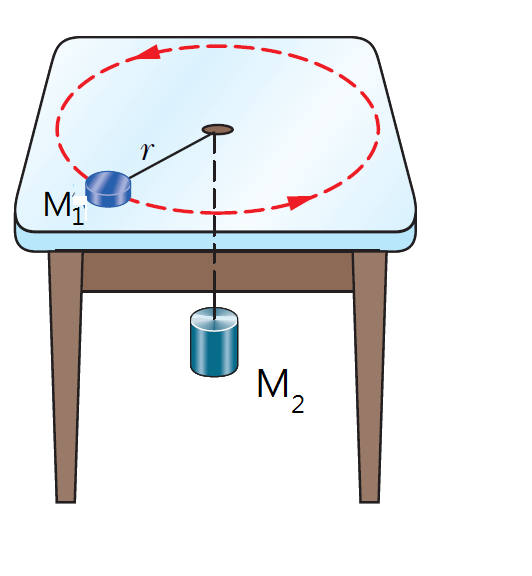A puck(冰球) of mass M_1 slides in a circle of radius r on a frictionless table while attached to a hanging cylinder of mass M_2 by a cord through a hole in the table (figure). What speed keeps the cylinder at rest? (01小題)
the speed v=_____ [M_1, M_2, r, g]
18: ANS:=sqrt(M_2*g*r/M_1)
Solution: