GP1-L07

Problem 1
A father racing his son has half the kinetic energy of the son, who has half the mass of the father. The father speeds up by 1 m/s and then has the same kinetic energy as the son. What are the original speeds of (a)the father and (b) the son?父親和兒子賽跑，其動能為兒子動能的一半，兒子質量只有父親質量的一半。父親速度增加\(1m/s\) 時，具有和兒子一樣的動能。問（a）父親和（b）兒子原來的速度？ (02小題)

(a)\(v_{father}\)=______m/s

01: ANS:=2.4

(b)\(v_{son}\)=______m/s

02: ANS:=4.8

Solution:

\(\frac{1}{2}m_f v_f^2=\frac{1}{2}(\frac{1}{2}m_s v_s^2)\)

\(\frac{1}{2}m_f=m_s\)

\(\frac{1}{2}m_f(v_f+1)^2=\frac{1}{2}m_s v_s^2\)

\(v_f^2-2v_f+1=0\)

\(v_f=2.4m/s\)

\(v_s=4.8m/s\)
Problem 2
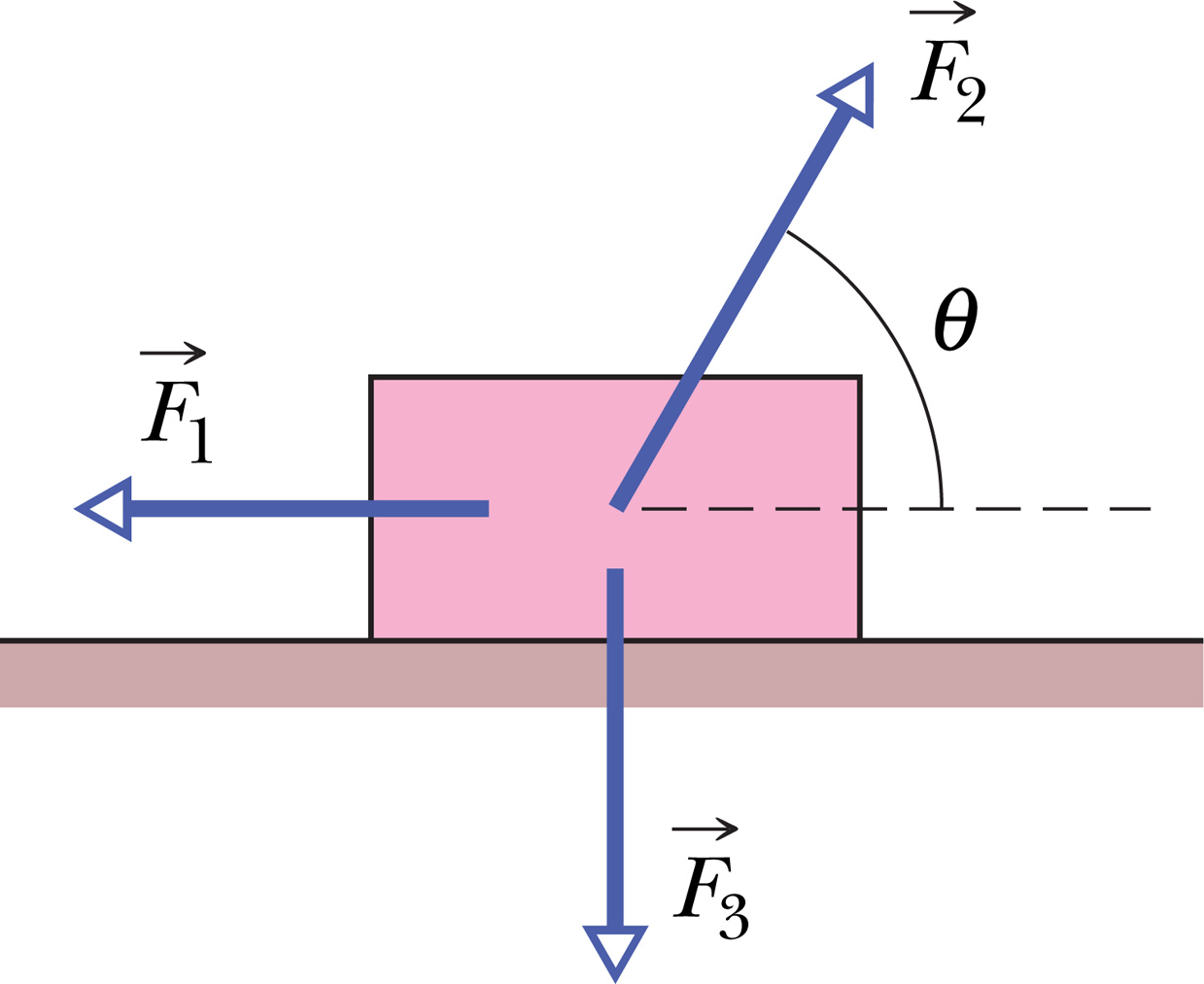The figure shows three force applied to a truck that moves leftward by 3 m over a frictionless floor. The force magnitudes are \(F_1=5\) N, \(F_2=9\) N,and \(F_3=3\) N , and the indicated angle is \(\theta=60^0\) . During the displacement, (a) what is the net work done on the truck by the three forces and (b) does the kinetic energy of the truck increase or decrease?
圖顯示了施加在無摩擦地板上向左移動3 m的卡車的三個力。力的大小為\(F_1 = 5 \)N，\(F_2 = 9 \)N和\(F_3 = 3 \) N，並且指示的角度為\(\theta = 60^o\)。 在位移期間，計算(a)卡車在這三個力的作用下的淨功，(b)卡車的動能是增加還是減少？ (02小題)

(a)work=_____J

03: ANS:=1.5

(b)increase=1, decrease=2

04: ANS:=1

Solution:

(a)\(W_1=(3)(5)=15J\)

\(W_2=(-9cos60^0)(3)=-13.5J\)

\(W_3=(3)(0)=0\)

\(W=15-13.5+0=+1.5J\)

(b)increase
Problem 3
A cord is used to vertically lower an initially stationary block of mass M at a constant downward acceleration of \(g/4\). When the block has fallen a distance d,find (a) the work done by the cord’s force on the block, (b) the work done by the gravitational force on the block, (c) the kinetic energy of the block, and (d) the speed of the block
繩索用於以恆定的向下加速度\(g/4\)垂直降低質量為M的初始物塊。當物塊下降了距離d時，計算(a)繩索在塊上的力所完成的功，(b)重力在物塊上的功所完成的功，(c)物塊的動能，以及(d)物塊速度。 (04小題)

(a)\(W_T\)=______Mgd

05: ANS:=-0.75

(b)\(W_g\)=______Mgd

06: ANS:=1

(c)K=______Mgd

07: ANS:=0.25

(d)if \(d=10m\), v=___m/s

08: ANS:=7

Solution:

(a)\(Mg-T=M\dfrac{g}{4}\)

\(T=\dfrac{3}{4}Mg\)

\(W_T=-Td=-\dfrac{3}{4}Mgd\)

(b)\(W_g=Mgd\)

(c)\(-\dfrac{3}{4}Mgd+Mgd=\dfrac{1}{4}Mgd\)

(d)\(E_K=\dfrac{1}{2}Mv^2=\dfrac{1}{4}Mgd\)

\(v=\sqrt{\dfrac{gd}{2}}=\sqrt{\dfrac{(9.8)(10)}{2}}=7m/s\)
Problem 4
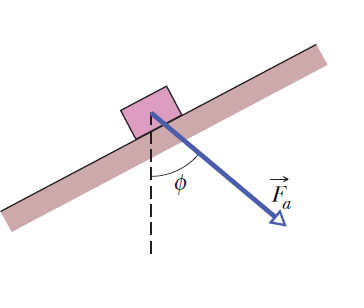In the figure, a constant force \(\vec{F}_a\) of magnitude 82 N is applied to a 3 kg shoe box at angle \(\phi=53^0\) , causing the box to move up a frictionless ramp at constant speed. How much work is done on the box by \(\vec{F}_a\) when the box has moved through vertical distance h=0.15 m ?
在圖中，大小為82 N的恆定力\(\vec{F}_a\)以角度\(\phi = 53^0 \)施加於3 kg的鞋盒，使鞋盒無摩擦地向上移動以恆定速度傾斜。當盒子經過垂直距離h = 0.15 m時，\(\vec{F}_a \)在盒子上做了多少功？ (01小題)

W=______J

09: ANS:=4.41

Solution:

\(W_a=+mgh=(3kg)(9.8m/s^2)(0.15m)=4.41J\)
Problem 5
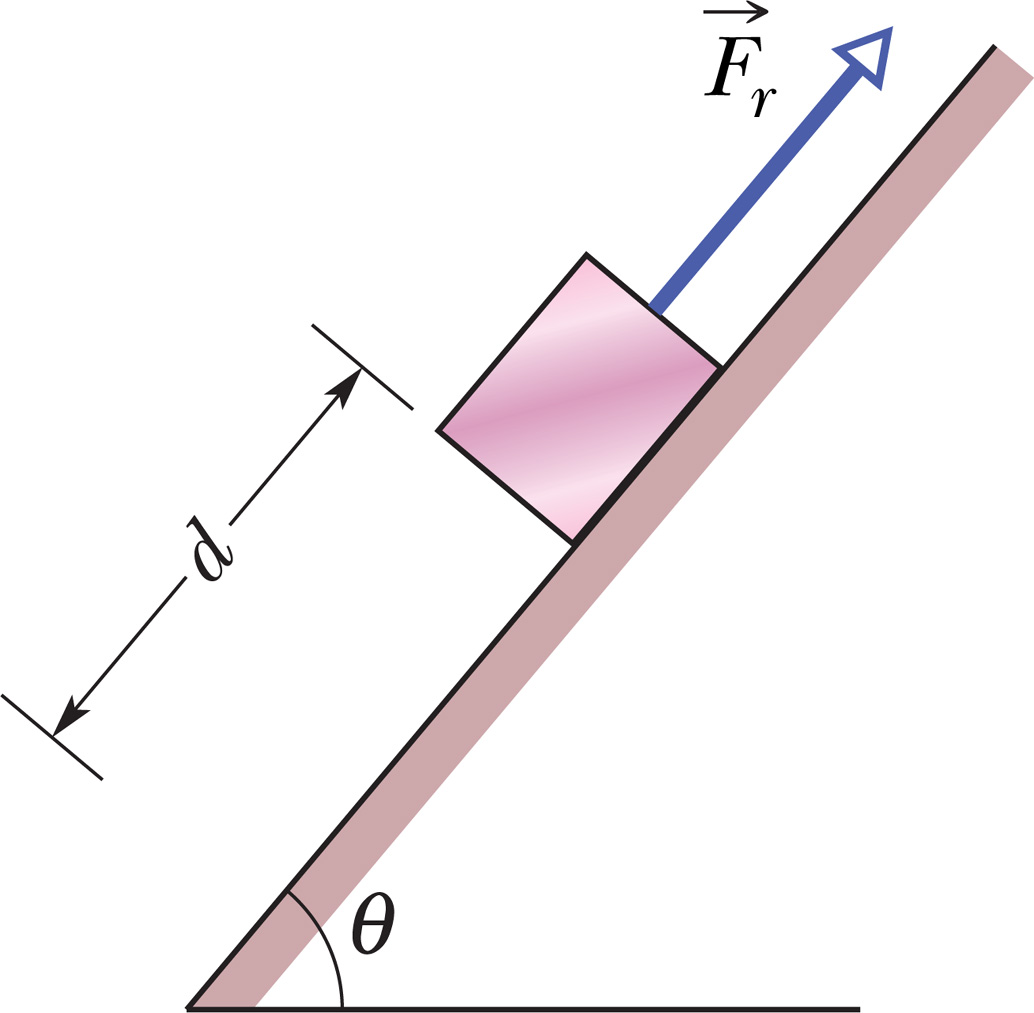In the figure, a block of ice slides down a frictionless ramp at angle \(\theta=50^0\) while an ice worker pulls on the block (via a rope) with a force \(\vec{F}_r\) that has a magnitude of \(50 N\) and is directed up the ramp. As the block slides through distance \(d=0.5m\) along the ramp, its kinetic energy increases by \(80 J\). How much kinetic energy will the block increase if the rope had not been attached to the block?
在圖中，一塊冰塊以無摩擦的坡度滑過角度\(\theta = 50^0 \)，而製冰工人利用繩索施力\(\vec{F}_r \)拉動一塊冰塊，其大小為50 N ，方向為沿著斜面向上。 當冰塊沿坡滑過距離d = 0.5 m時，其動能增加80 J。 如果未將繩索連接冰塊，其動能將會增加多少？ (01小題)

the kinetic energy will increase ______ J

10: ANS:=105

Solution:

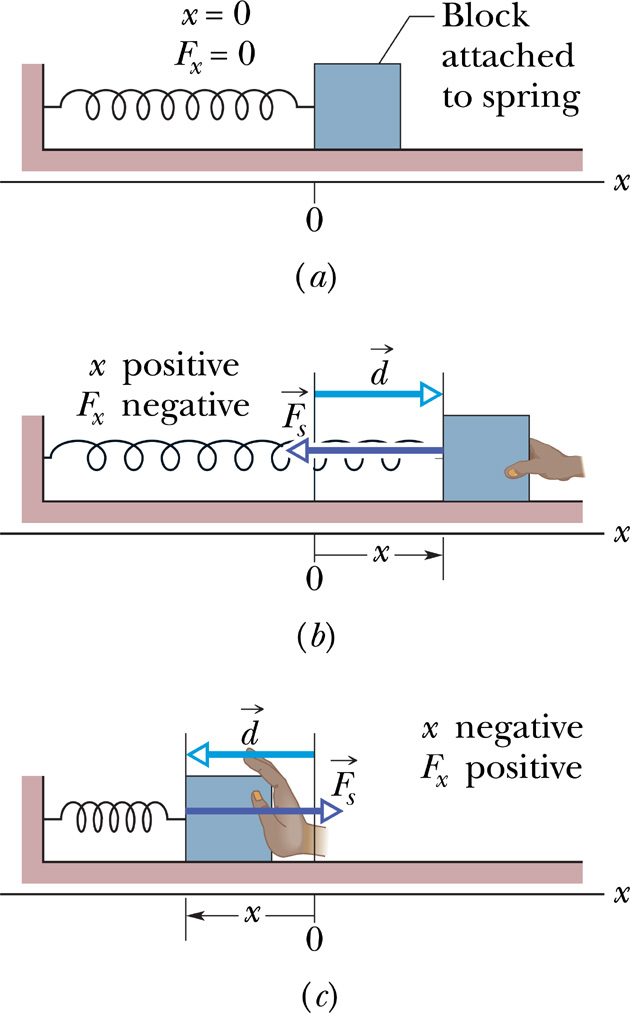the work by the rope:\(W=(-50N)(0.5m)=-25J\). The kinetic energy will be 25J greater if it is not attached to the rope. So the increase will be 80+25=105 J
Problem 6
A spring and block are in the arrangement of the figure. When the block is pulled out to x= +4 cm , we must apply a force of magnitude 360 N to hold it there. We pull the block to x= 11 cm and then release it. How much work does the spring do on the block as the block moves from +5 cm to (a) +3 cm , (b) -3 cm , (c) -5 cm, and (d) -9 cm ?
彈簧和滑塊處於該圖的佈置中。 當將塊拉出到x = +4 cm時，我們必須施加360 N的力將其固定在那裡。 我們將塊拉到x = 11厘米，然後釋放它。 當彈簧塊從+5 cm移動到（a）+3 cm，（b）-3 cm，（c）-5 cm和（d）-9 cm時，彈簧在彈簧塊上做了多少工作？ (04小題)

(a)\(W_s\)=______J

11: ANS:=7.2

(b)\(W_s\)=______J

12: ANS:=7.2

(c)\(W_s\)=______J

13: ANS:=0

(d)\(W_s\)=______J

14: ANS:=-25

Solution:

\(F=kx\)

\(k=\dfrac{F}{x}=\dfrac{360N}{4cm}=90N/cm=9 \times 10^3 N/m\)

彈簧做的功\(W_s=\dfrac{1}{2}k(x_i^2-x_f^2)\)

(a)\(W_s=\frac{1}{2}(9 \times 10^3 N/m)[(0.05m)^2-(0.03m)^2]=7.2J\)

(b)\(W_s=\frac{1}{2}(9 \times 10^3 N/m)[(0.05m)^2-(-0.03m)^2]=7.2J\)

(c)\(W_s=\frac{1}{2}(9 \times 10^3 N/m)[(0.05m)^2-(-0.05m)^2]=0J\)

(d)\(W_s=\frac{1}{2}(9 \times 10^3 N/m)[(0.05m)^2-(-0.09m)^2]=-25J\)
Problem 7
The only force acting on a 2 kg body as it moves along a positive x axis has an x component \(F_x=-6x \) N , with x in meters. The velocity at x=3 m is 8 m/s . (a) What is the velocity of the body at x=4 m? (b) At what positive value of x will the body have a velocity of 5 m/s ?
沿正x軸移動時作用在2 kg物體上的唯一力是x分量\(F_x = -6x \) N ，其中x以米為單位。(x = 3 m 處的速度為8 m/s。 (a)物體在x=4 m 處的速度是多少？ (b)x在哪個正值處，物體的速度為5 m/s? (02小題)

(a)v=______m/s

15: ANS:=6.6

(b)x=______m

16: ANS:=4.7

Solution:

(a)從 \(x=3m\) 移動到 \(x=4m\) 做功

\(W=-3(x_2^2-x_1^2)=-3(4^2-3^2)=-21J\)

\(W=\Delta K=\dfrac{1}{2}m(v_2^2-v_1^2)\)

\(v_2=\sqrt{\dfrac{2W}{m}+v_1^2}=\sqrt{\dfrac{2(-21J)}{2kg}+(8m/s)^2}=6.6m/s\)

(b)\(W=-3(x_2^2-x_1^2)=\dfrac{1}{2}m(v_2^2-v_1^2)\)

\(x_2=\sqrt{-\dfrac{m}{6}(v_2^2-v_1^2)+x_1^2}=\sqrt{-\dfrac{2kg}{6}[(5m/s)^2-(8m/s)^2]+(3m)^2}=4.7m\)
Problem 8
A single force acts on a \(3\) kg particle-like object whose position is given by \(x=3t-4t^2+1t^3\) , with \(x\) in meters and \(t\) in seconds. Find the work done on the object by the force from \(t=0\) to \(t=4\) s.
單一力作用於\(3\) kg物體，其位置的時間函數\(x = 3t-4t ^ 2 + 1t ^ 3 \)，其中\(x \)以m為單位，而\(t \) 以秒為單位。 計算從\(t = 0 \)到\(t = 4 \)秒，力在物體上所做的功。 (01小題)

W=___J

17: ANS:=528

Solution:

\(v=\dfrac{dx}{dt}=3-8t+3t^2\)

\(v(t=0)=3m/s\)

\(v(t=4)=19m/s\)

\(\Delta K=\dfrac{1}{2}m(v_f^2-v_i^2)=528J\)...動能變化即所做的功

\(W=528J\)
Problem 9
A 0.30 kg object sliding on a horizontal frictionless surface is attached to one end of a horizontal spring (k = 500 N/m) whose other end is fixed. The object has a kinetic energy of 10 J as it passes through its equilibrium position (the point at which the spring force is zero). (a) At what rate is the spring doing work on the object as the object passes through its equilibrium position? (b) At what rate is the spring doing work on the object when the spring is compressed 0.10 m and the object is moving away from the equilibrium position?
將在水平無摩擦表面上滑動的0.30千克物體連接到水平彈簧（k = 500 N/m）的一端，另一端固定。 當物體通過其平衡位置（彈簧力為零的點）時，其動能為10J。 （a）當物體通過其平衡位置時，彈力作用於物體的功率？ （b）當彈簧被壓縮0.10 m並且物體在遠離平衡位置的方向運動，彈力作用於物體的功率？ (02小題)

(a)as the object passes through equilibrium position, power P=____ W

18: ANS:=0

(b)when the spring is compressed 0.10 m, the power P=____ W

19: ANS:=-350

Solution:

Problem 10
A force of 5.0 N acts on a 15 kg body initially at rest. Compute the work done by the force in (a) the first, (b) the second, and (c) the third seconds and (d) the instantaneous power due to the force at the end of the third second.
5.0 N的力最初在靜止時作用在15公斤的物體上。 計算在(a)第一秒內，(b)第二秒內，(c)第三秒內力所做的功。(d)第3秒結束時的力造成的瞬時功率。 (04小題)

(a)P=____ W

20: ANS:=0.83

(b)P=____ W

21: ANS:=2.5

(c)P=____ W

22: ANS:=4.2

(d)P=____ W

23: ANS:=5.0

Solution: