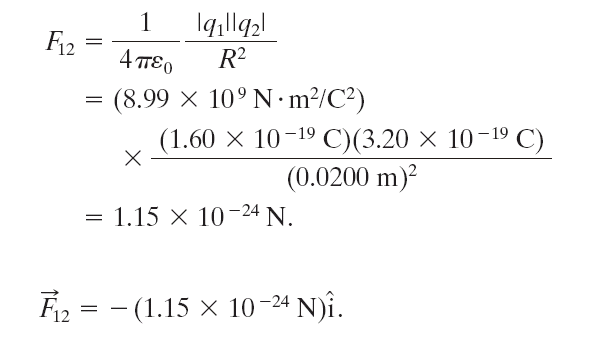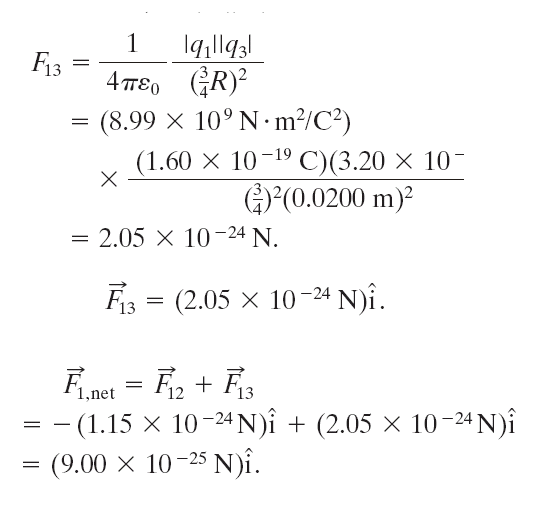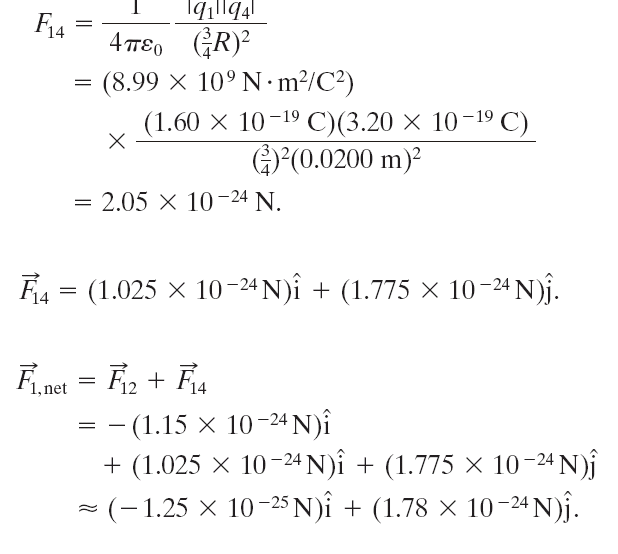電力也稱庫倫力
物質在摩擦起電後會帶了兩種不同的電性
用玻璃與絲巾摩擦以後玻璃棒上所帶的電與毛皮摩擦琥珀所得的電不一樣,帶同類電性的物體會互相排斥,帶有不同電性的物體之間會相互吸引。法國科學家杜菲認為每一種物體帶有兩種流體,各有不同的電性,當摩擦兩個物體的時候,帶有不同電性的流體會在物體之間流動。當物體的兩種流體的量不相等的時候,就會讓物體帶電。現在我們知道這種流體被稱為電荷,並且當我們磨擦兩種物體的時候,會轉移的電荷稱為電子。所有的物體都是由原子構成,而原子的主要成員是位於原子的正中央帶正電的原子核,吸引外圍的帶負電的電子。原子核由兩種基本的粒子組成,其中質子帶正電,中子不帶電,原子核的正電就是來自於質子。磨擦兩個不同物體的時候,原子外圍的電子會從一個物體轉移到另外一個物體,具有過多電子的物體就帶了負電,失去電子的物體就帶的正電。電荷守恆
電子的轉移造成物體帶電,但是整體電荷的總量並沒有改變,這個現象稱為電荷守恆。電荷守恆與能量守恆、動量守恆、角動量守恆一樣都是物理世界中非常重要的守恆定律。基本電量
電量又是一個新的物理量,描述這個物理量我們所使用的單位是庫倫,這是Si國際單位系統認定的單位。電子是一個基本粒子,它所帶的電量也是一個基本電量,電量的大小是\(1.6 \times 10^{-19}\) C(庫倫)。基本電量是一個物體所能帶電的最小電量,並且也是不可分割的電量,所有物體所帶的電量都是這個基本電量的整數倍。證實這個結果的重要實驗就是密立根根的油滴實驗。質子所帶的電量與電子相同都是基本電量,但是質帶的是正電。懸掛起來的棒子
當玻璃與絲巾摩擦的時候,電子會從玻璃轉移到絲巾,所以摩擦後的玻璃會帶正電。相對的,琥珀與毛皮摩擦之後,會從毛皮獲得電子,所以會帶負電。若將摩擦過後的玻璃棒靠近琥珀會發現玻璃棒吸引琥珀,這就是異性電相吸。如果將磨擦過後的玻璃棒懸掛起來,用另外一個摩擦過後的玻璃棒與懸掛起來的棒子靠近,可以觀察到兩個玻璃棒互相排斥,這就是同性電互相排斥。庫倫定律
電荷與電荷之間的交互作用力也稱為庫倫力,因為第一個對這個力量做出定量測量的科學家,就是法國科學家庫倫,他在1785年的時候測量出兩個電荷之間的交互作用力所滿足的定律,如下面的公式所呈現 \[\vec{F}=\dfrac{k q_1 q_2}{r^2} \hat{r}; \quad 8.99 \times 10^9 \,kg⋅m^3⋅s^{−2}⋅C^{−2}\] 其中k稱為庫倫常數,\(q_1, \, q_2\)是兩個電荷所帶的電量,\(r\)是兩個電荷之間的距離,其中的單位向量\(\hat{r}\)是兩個點電荷連線的單位向量。電力也是一個向量,不但有大小也有方向,電力的方向在電荷的連線上,也是一種向心力。電力的大小與電量成正比與距離的平方成反比,這個平方反比定律在牛頓的重力定律當中已經出現過,大自然非常有趣,再一次選擇距離的平方反比定律來實現兩個電荷之間的交互作用力。庫倫常數又可寫成下面的形式: \[k=\dfrac{1}{4 \pi \varepsilon_0}\] 其中\(\varepsilon_0\)稱為真空的電容率(permittivity of vacuum),或「真空介電常數」,其數值\[\varepsilon_0=8.85 \times 10^{-12}.\]重力和庫倫力比較
我們可以考慮電子與質子結合的兩種吸引的力量:重力和庫倫力。考慮他們之間的重力,我們要先知道電子與質子的質量和他們之間的距離,同樣的我們可以利用電子與質子所帶的電量,利用庫倫定律來計算庫倫吸引力,兩者計算的公式如下: \[\dfrac{F_e}{F_g}=\dfrac{k e^2}{G m_e m_p} \simeq 2 \times 10^{40}\] 我們的計算結果顯現,庫侖的電荷之間的吸引力(庫倫力)比因為質量而來的重力吸引大的10的40次方倍也就是庫倫力比重力大了40個數量級這個結果顯示形成物質的基本結構是有比較強的電力交互作用所決定但是因為這種力量也有可能是排斥的力量(同性電荷),因此如果我們要考慮天文現象或者宇宙結構等問題,就必須考慮只有吸引力的重力。線性疊加原理
上面公式所呈現的庫侖定律是針對兩個電荷之間的電力作用,但是如果空間中有許多的電荷,那麼其中一個電荷所受的所有電力的總和,是該電荷與其他所有電荷的庫侖力的向量總和,這個性質非常重要,稱為線型疊加原理。導體和絕緣體
我們一般可以根據電荷穿過材料的能力對材料進行分類。 導體是電荷可以自由移動的材料,包括金屬(如普通燈線中的銅)、人體和自來水。非導體-也稱為絕緣體-是電荷不能自由移動的材料。 例如包括橡膠(例如普通燈線上的絕緣層)、塑料、玻璃。半導體是介於導體和絕緣體之間的材料;例如包括計算機晶片中的矽和鍺。超導體是完美的導體材料,可以讓電荷不受阻礙地移動。導體和絕緣體的特性取決於原子的結構和電學性質。原子由帶正電的質子、帶負電的電子和電中性中子組成。質子和中子緊密地聚集在一個中央原子核中。單個電子的電荷和單個質子的電荷大小相同,但符號相反。因此,電中性原子包含相等數量的電子和質子。電子被保持在原子核附近,因為它們的電符號與原子核中的質子相反,因此被原子核吸引。當像銅這樣的導體的原子聚集在一起形成固體時,它們的一些最外層(也是最鬆散的)電子會在固體內自由遊蕩,留下帶正電的原子(正離子)。我們稱移動電子為傳導電子(導電電子,conducting electrons)。非導體中的自由電子很少。
導體的感應生電
 利用圖中的實驗我們可以證明電荷在導體中的遷移現象。在圖中我們把一個電中性的銅棒用絕緣的細線懸掛起來,因此銅棒處在一個隔離的狀態,不會因為自己是導體而流失傳導電子。將一帶負電的塑料棒靠近金屬銅棒的左端,塑膠棒上的負電荷會排斥銅棒左端的傳導電子。部分傳導電子因排斥而移動到銅棒的遠端,使近端電子缺乏,因此帶有不平衡的正電荷。該正電荷被塑料棒中的負電荷吸引,因此這兩端會彼此吸引而互相靠近。儘管銅棒仍然是中性的,但它具有感應電荷(induced charges),意味著銅棒中的部分電荷由於附近存在電荷而被分離。類似地,如果將帶正電的玻璃棒靠近電中性銅棒的一端,銅棒中的傳導電子會被吸引到該端。該端帶負電,另一端帶正電,因此再次重置銅棒上的感應電荷 。雖然銅棒仍然是中性的,但是因為異性電相吸近,近端的銅棒仍然會向帶正電玻璃棒靠近。請注意,只有帶負電荷的傳導電子才能移動;正離子固定在位,因此,銅棒只有通過去除負電荷才能使其帶正電。
利用圖中的實驗我們可以證明電荷在導體中的遷移現象。在圖中我們把一個電中性的銅棒用絕緣的細線懸掛起來,因此銅棒處在一個隔離的狀態,不會因為自己是導體而流失傳導電子。將一帶負電的塑料棒靠近金屬銅棒的左端,塑膠棒上的負電荷會排斥銅棒左端的傳導電子。部分傳導電子因排斥而移動到銅棒的遠端,使近端電子缺乏,因此帶有不平衡的正電荷。該正電荷被塑料棒中的負電荷吸引,因此這兩端會彼此吸引而互相靠近。儘管銅棒仍然是中性的,但它具有感應電荷(induced charges),意味著銅棒中的部分電荷由於附近存在電荷而被分離。類似地,如果將帶正電的玻璃棒靠近電中性銅棒的一端,銅棒中的傳導電子會被吸引到該端。該端帶負電,另一端帶正電,因此再次重置銅棒上的感應電荷 。雖然銅棒仍然是中性的,但是因為異性電相吸近,近端的銅棒仍然會向帶正電玻璃棒靠近。請注意,只有帶負電荷的傳導電子才能移動;正離子固定在位,因此,銅棒只有通過去除負電荷才能使其帶正電。
導體球
如果將多餘電荷(過多的正電荷和負電荷,造成導體正負電荷不平衡的多餘電荷)放置在由導電材料製成的球上,則多餘電荷會均勻地分佈在(外)表面上。例如,如果我們將多餘的電子放在球形金屬球上,這些電子會相互排斥並趨於分開,在可用表面上擴散,直到它們均勻分佈。這種分布使所有多餘電子對之間的距離最大化,以降低彼此之間的排斥力。根據球殼定理,殼將吸引或排斥外部電荷,就好像殼上所有多餘的電荷都集中在其中心一樣。如果我們從球形金屬殼中去除負電荷,則所產生的殼的正電荷也會均勻地分佈在殼的表面上。例如,如果我們移除 \(n\)個電子,則有\(n\)個正電荷位點(缺少一個電子的位點)均勻分佈在殼上。根據球殼定理,殼將再次吸引或排斥外部電荷,就好像所有殼的多餘電荷都集中在其中心一樣。數學工具
我們即將開始電磁學的學習再學習之初,同學們一定要先複習一些數學工具,否則在後面的學習中你會經常犯下一些計算上的錯誤,甚至會導致觀念上的錯誤。第一個要注意的重點就是電力、電場磁力和磁場都是向量,所以同學們務必要熟悉向量的計算,包括向量的內積、向量的投影、向量的長度、向量的夾角、單位向量的概念、向量的外積等等。並且要有場的觀念。場的觀念又跟我們在波動現象當中所學到的有關,因此同學們務必熟悉這些數學工具。首先我們先強調場的概念。在電學當中我們已經知道電荷是造成電力的原因,即使空間中只有一個電荷存在,我們都相信這個電荷會在空間中建立起一個電場。雖然我們要到下一個單元才會介紹電場,但是我們在普通物理1已經學過重力和重力場,因此我們對電場的想像可以從重力場的概念加以延伸。只要有電荷存在空間中任何一個位置都可能有電場存在,因此我們想像空間中有許多的箭頭,這個箭頭的方向的大小就在描述這個電場向量。通常我們會用兩個向量分別用來描述場的源頭跟場的位置。場的源頭就是電荷的位置向量,場的位置就用一個從坐標原點延伸到場點的向量來表示,同學們不要弄混了這兩個位置向量。如同我們前面所講的,電力具有線性疊加原理,因此如果空間中有許多電荷存在,對空間中任何一個場位置計算其電場,就要對所有這些電荷進行加法或積分。當我們在進行電荷的加法的時候,請注意場點的位置向量是固定的,而不同的電荷隨著所在位置的不同,所貢獻的電場也有所不同,因此在進行求和(積分)的時候電荷的位置向量是一個變量。
向量運算的複習
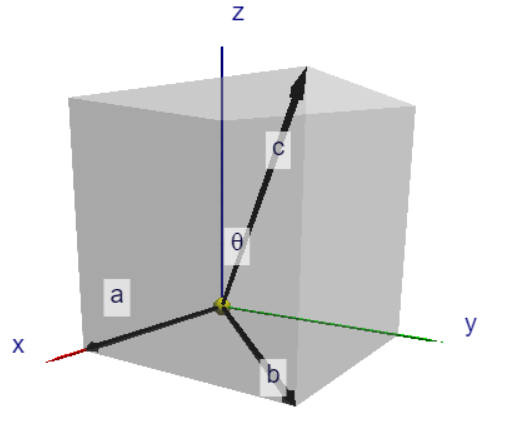 假設我們有邊長為1的立方體,如圖所示。其中向量\(\vec{a}, \, \vec{b}, \, \vec{c}\)分別是邊長向量,面對角線向量和體對角線向量。我們可以針對這些向量進行下面的向量運算:
假設我們有邊長為1的立方體,如圖所示。其中向量\(\vec{a}, \, \vec{b}, \, \vec{c}\)分別是邊長向量,面對角線向量和體對角線向量。我們可以針對這些向量進行下面的向量運算:
- \(\vec{a}=(1,0,0), \,\, \vec{b}=(1,1,0) \,\, \vec{c}=(1,1,1)\)
- \(|\vec{c}|=\sqrt{1^2 + 1^2 + 1^2}=\sqrt{3}\)
- \(\hat{c}=\dfrac{\vec{c}}{|\vec{c}|}=\dfrac{1}{3}(\hat{i}+\hat{j}+\hat{k})\)
- \(\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}| \cos \theta = a_x b_x +a_y b_y +a_z b_z=1+0+0=1 \\ \theta 是\vec{a}與\vec{b}的夾角\)
- \(\vec{a}與\vec{b}的夾角,\theta=\cos^{-1} \left[\dfrac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|} \right] \)
- \( \vec{d}=\vec{b} \times \vec{c} = \begin{vmatrix} \hat{i}&\hat{j}&\hat{k}\\ b_x&b_y&b_z \\ c_x&c_y&c_z\end{vmatrix} =(b_y c_z - b_z c_y) \hat{i} + (b_z c_x - b_x c_z) \hat{j} + (b_x c_y - b_y c_x) \hat{k} \\ = \begin{vmatrix} \hat{i}&\hat{j}&\hat{k}\\ 1&1&0 \\ 1&1&1 \end{vmatrix} = \hat{i} - \hat{j} \)
範例-1:點電荷的靜電力
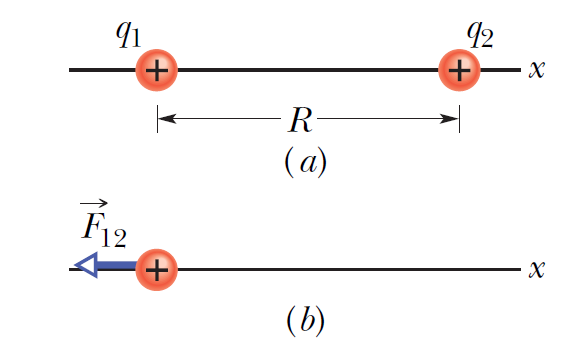
|
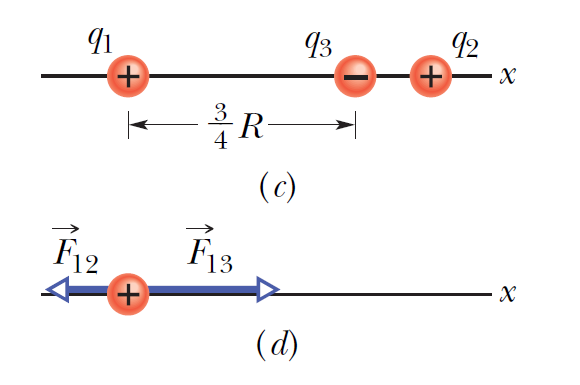
|
|
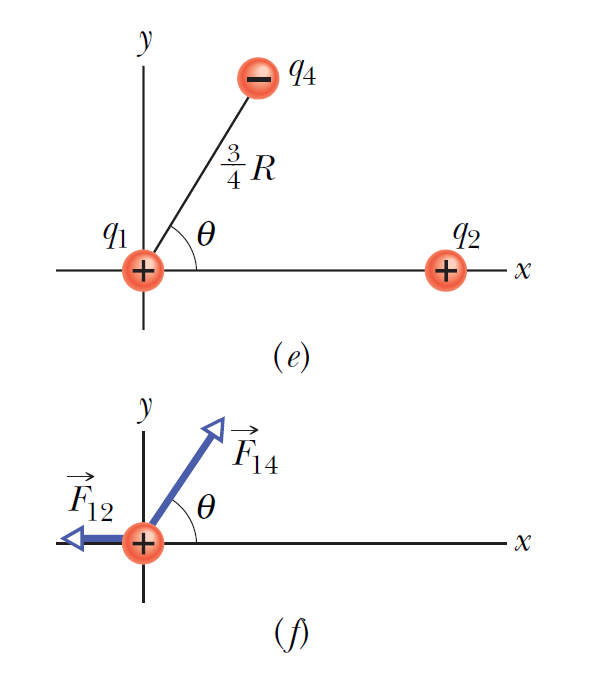 |
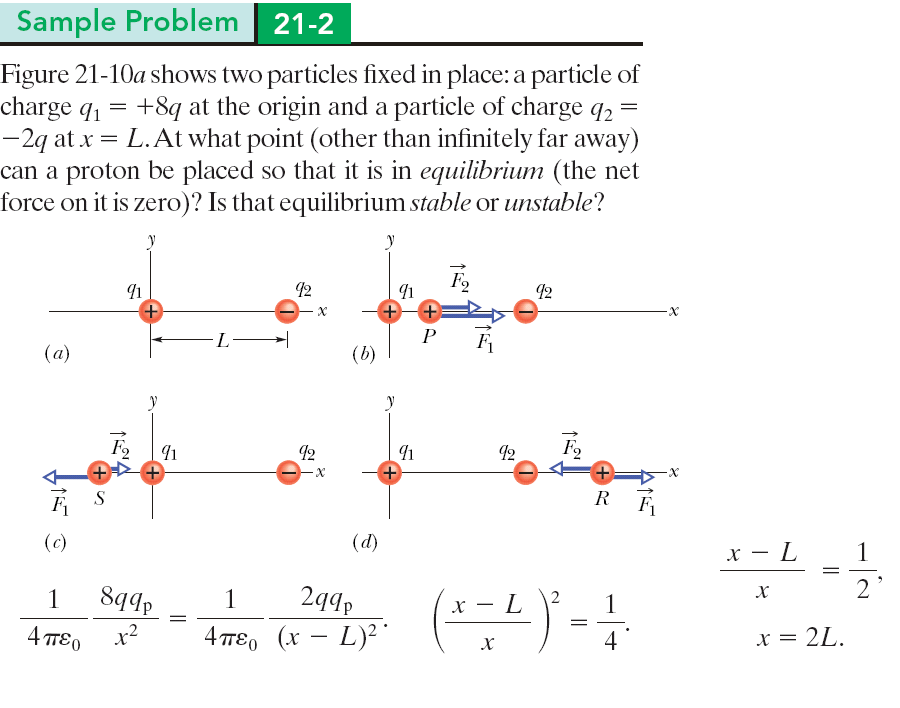
範例-2:點電荷的平衡
|
The figure shows two particles fixed in place: a particle of charge \(q_1=+8q\) at the origin and a particle of charge \(q_2=-2q\) at \(x=L\). At what point (other than infinitely far away) can a proton be placed so that it is in equilibrium (the net force on it is zero)? Is that equilibrium stable or unstable? 該圖顯示了兩個固定在適當位置的粒子:原點處的帶電粒子 \(q_1=+8q\) 和 \(x=L\) 處的帶電粒子 \(q_2=-2q\)。 在什麼點(除了無限遠)可以放置一個質子以使其處於平衡狀態(其上的合力為零)? 這種平衡是穩定的還是不穩定的? |
|
範例-3:導電球體的電荷移動
|
In Fig. a, two identical, electrically isolated conducting spheres \(A\) and \(B\) are separated by a (center-to-center) distance \(a\) that is large compared to the spheres. Sphere \(A\) has a positive charge of \(+Q\), and sphere \(B\) is electrically neutral. Initially, there is no electrostatic force between the spheres. (Assume that there is no induced charge on the spheres because of their large separation.) (a) Suppose the spheres are connected for a moment by a conducting wire. The wire is thin enough so that any net charge on it is negligible. What is the electrostatic force between the spheres after the wire is removed? (b) Next, suppose sphere \(A\) is grounded momentarily, and then the ground connection is removed. What now is the electrostatic force between the spheres? 在圖 a 中,兩個相同的、電隔離的導電球體 \(A\) 和 \(B\) 被(中心到中心)距離 \(a\) 隔開,該距離比球體大。 球體\(A\) 帶正電荷\(+Q\),球體\(B\) 是電中性的。 最初,球體之間沒有靜電力。 (假設球體上沒有感應電荷,因為它們的間距很大。) (a) 假設球體通過導線連接片刻。 電線足夠細,因此其上的任何淨電荷都可以忽略不計。 拆線後球體之間的靜電力是多少? (b) 接下來,假設球體 \(A\) 暫時接地,然後移除接地連接。 現在球體之間的靜電力是多少?
(a)\[F=\dfrac{1}{4 \pi \varepsilon_0} \dfrac{(Q/2)(Q/2)}{a^2}=\dfrac{1}{16 \pi \varepsilon_0} \dfrac{(Q^2)}{a^2}\]
(b)因為球體 A 帶正電,總電荷為 Q/2 的電子從地面向上移動到球體上(圖 d),使球體的電荷為 0(圖 e)。 因此,兩個球體之間沒有靜電力。
|
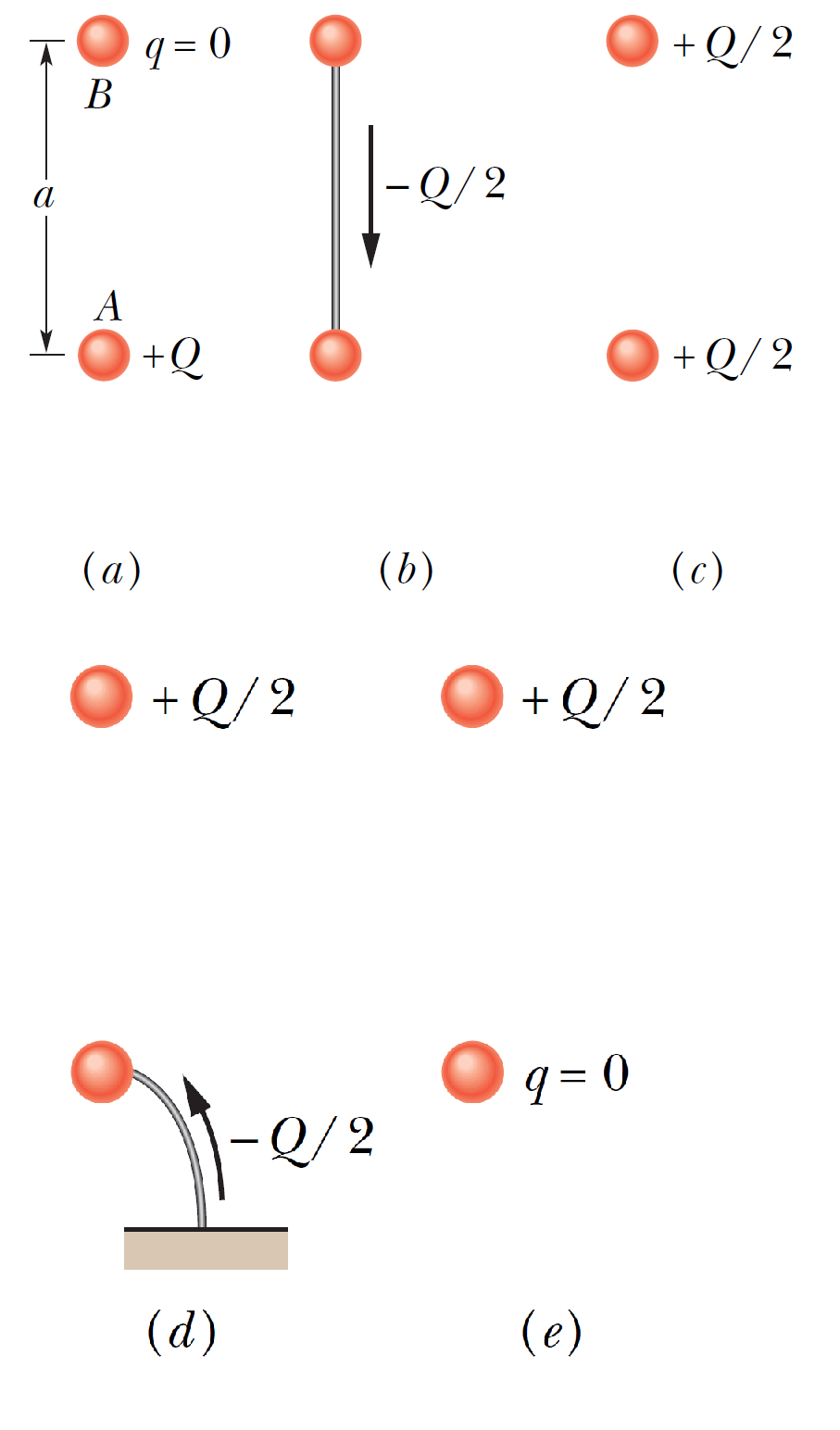
|
範例-4:點電荷的平衡
|
The nucleus in an iron atom has a radius of about \(4.0 \times 10^{-15}\) m and contains 26 protons. (a) What is the magnitude of the repulsive electrostatic force between two of the protons that are separated by \(4.0 \times 10^{-15}\) m? (b) What is the magnitude of the gravitational force between those same two protons? 鐵原子中的原子核的半徑約為 \(4.0 \times 10^{-15}\) m 並包含 26 個質子。 (a) 相隔 \(4.0 \times 10^{-15}\) m 的兩個質子之間的排斥靜電力的大小是多少? (b) 這兩個質子之間的引力有多大? |

|
授課教師
陳永忠 ycchen@thu.edu.tw