電場

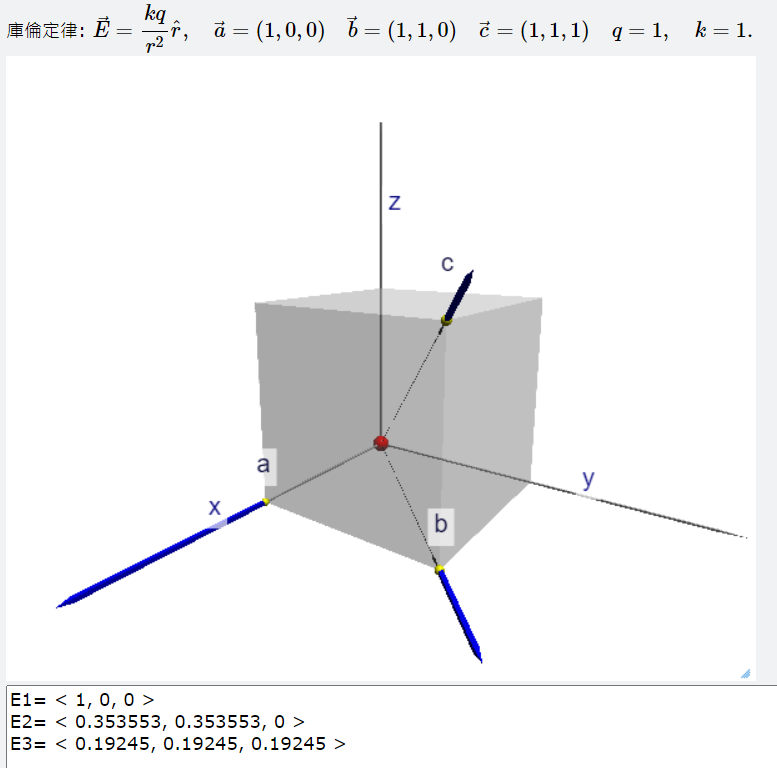
庫倫定律

我們知道電荷的存在會在空間中建立起一個電場，最簡單的電荷源就是電點荷。描述單一一個電荷所建立的電場的基本定律就是庫倫定律。最簡單形式的庫侖定律就是描述兩個點電荷\(q 與 q_1\)之間的靜電力其公式如下： \[\vec{F}=\frac{k q q_1}{r^2}\hat{r}=\frac{k q q_1}{r^3}\vec{r} \] 請注意在上面這個公式中我們用了一個非常重要的向量關係，那就是位置向量(\(\vec{r}\))的單位向量(\(\hat{r}\))等於位置向量除以位置向量的長度(\(|\vec{r})\))，而且還要注意到上面這個公式中，是以坐標系統的原點就在點電荷(\(q_1\)的位置，來描述\(q\)所受到的靜電力。如果我們在空間中有許多的電荷，那麼這個公式就不適合來描述這樣的情況。所以比較好的庫倫定律的寫法應該是下面的公式。

空間中有許多個電荷，每一個電荷的電量用\(q_i\)來表示，而座標的原點不在特定的點電荷\(q_i\)上面，而是可以根據我們的問題選擇一個適合的位置作為座標的原點，一旦選定了原點，點電荷\(q_i\)就有自己的位置向量(\(\vec{r}_i\))，電荷\(q\)位置向量是以\(\vec{r}\)來表示。電荷\(q\)受到所有其他電荷靜電力的總和\(\vec{F}\)可以的用線性疊加原理寫成： \[\vec{F}=\sum_{i} \frac{k q q _i}{|\vec{r}-\vec{r}_i|^3}(\vec{r}-\vec{r}_i)=q \left[ \frac{k q _i}{|\vec{r}-\vec{r}_i|^3}(\vec{r}-\vec{r}_i) \right] .\]

電場的定義

從空間中多個電荷對同一個點電荷\(q\)的庫倫作用力的公式可以看出來，如果我們把這個電荷的電量放在求和的外面，那麼剩下的向量與電荷\(q\)的電量無關，只跟電荷\(q\)的位置\(\vec{r}\)，還有其他所有電荷的電量\(q_i\)和位置\(\vec{r}_i\)有關，這個向量\(\vec{E}\)我們就稱為所有電荷在空間中所建立的電場。根據這個定義我們可以寫下下面這個公式： \[\vec{E}=\dfrac{\vec{F}}{q}.\] 根據電場的定義我們知道電場的SI單位是N/C，這個單位等同於伏特除以公尺，V/m，我們在後面介紹電位的時候還會再說明。
一個點電荷在空間中所建立的電場可以寫成 \[\vec{E}=\frac{kq_1}{r^2}\hat{r}=\frac{kq_1}{r^3}\vec{r} \] 其中座標的原點選擇在點電荷的位置。多電荷所建立的電場可以寫成： \[\vec{E}=\sum_{i} \frac{kq_i}{|\vec{r}-\vec{r}_i|^3}(\vec{r}-\vec{r}_i) \] 電場本身是一個向量(\(\vec{E}\))，其方向及大小與空間中的位置有關，在\(\vec{r}\)的位置點的電場向量是\(\vec{r}\)的函數，當然也是\(x, \, y, \, z\)的函數：\[\vec{E}=\vec{E}(\vec{r})=\vec{E}(x,y,z)=E_x(x,y,z)\hat{i}+E_y(x,y,z)\hat{j}+E_z(x,y,z)\hat{k}\] 在我們下面的計算中就是反覆的應用這個電場公式來計算單一一個點電荷，或是有多個電荷分佈成不同的幾何形狀時，在空間中分別建立起的電場。

電偶極矩的電場

如果我們有一個正電荷\(+q\)和一個負電荷\(-q\)分隔一段距離\(d\)形成一個所謂的電偶極\(\vec{p}\)，乘積 \(p=qd\)，涉及電偶極子的兩個固有屬性 \(q\) 和 \(d\)，是電偶極矩的向量的大小 \(|\vec{p}|\) 偶極子（單位是庫侖-米）， 向量\(\vec{p}\) 的方向被認為是從偶極子的負端到正端。我們可以使用此方向來指定電偶極子的方向。如果我們說考慮的場點位在\(+z\)的方向，也就是電偶極矩的直線方向上，那麼透過兩個電荷的電場向量加法，在遠離這個電偶極的地方去測量電場的話，我們可以得到電偶極矩在這個方向上的電場\(E=\dfrac{2kqd}{z^3}\)，電場的大小隨著遠離電偶極的距離是3次方反比定律： \[電偶極矩的電場行為:\quad E \propto 1/r^3\]如果我們所考慮的點是沿著\(+x\)軸方向，也就是電偶極矩的垂直平分線上，我們也會得到類似的結果：電場仍然會隨著距離三次方反比定律。


電荷圓環所產生的電場

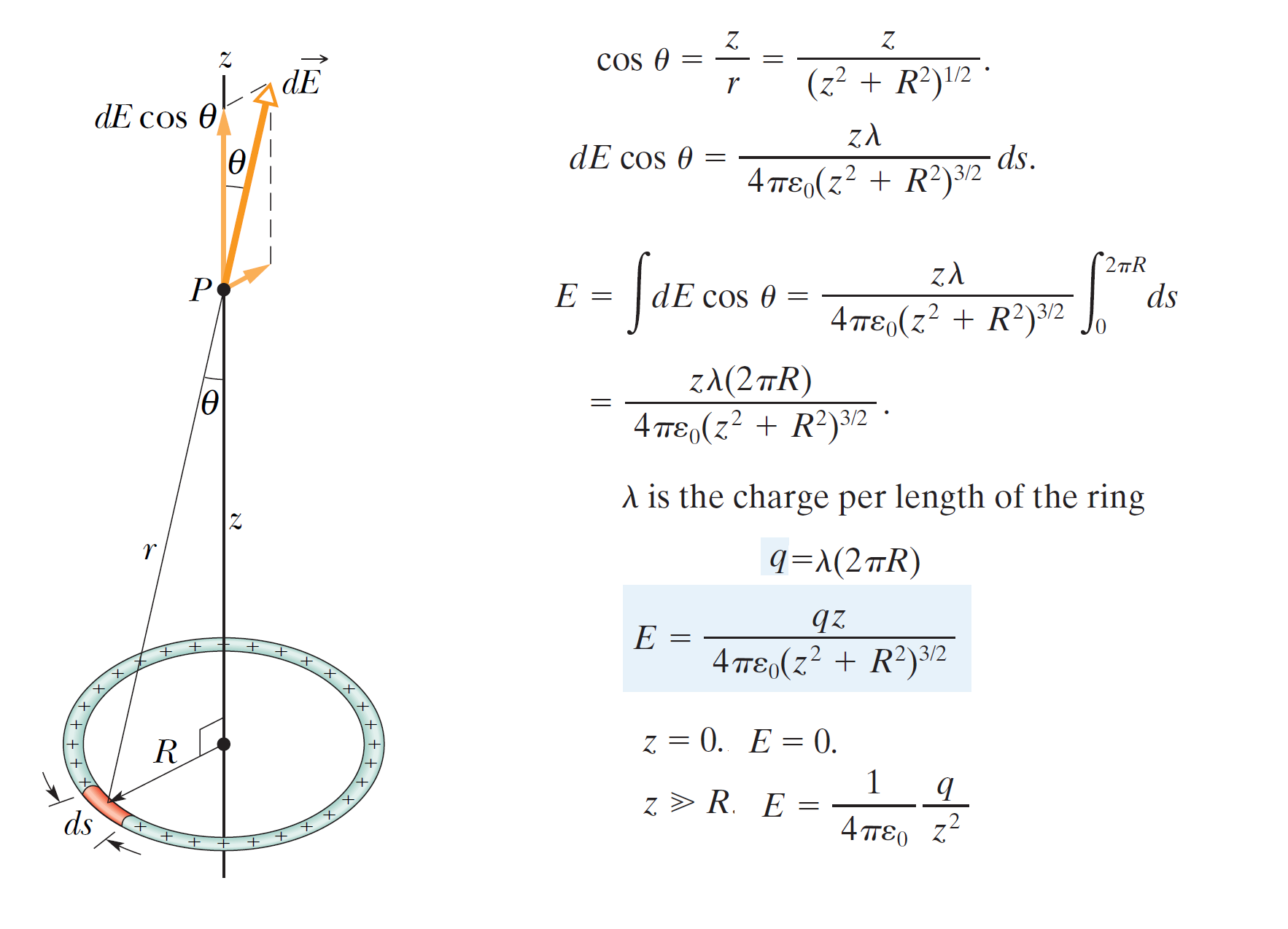如圖所示，如果我們有一個連續的電荷分佈在一個圓環上，圓環的半徑是\(R\)，總電量是\(q\)，也就是電荷的線密度\(\lambda=\dfrac{q}{2 \pi R}\)。我們可以利用積分計算通過這個圓環的中心並與圓環面垂直的中心軸，距離圓心\(z\)的位置的電場。從圖形中看到所有電荷相對於\(P\)點是對稱均勻分佈的，因此電荷在\(P\)點的電場貢獻只有\(+z\)軸方向的分量，與\(z\)軸垂直的\(x,\, y\)分量必然互相抵銷，沒有貢獻，也就是\(P\)點的電場方向必然是在\(+z\)的方向： \[ E=\dfrac{qz}{4 \pi \varepsilon_0 (z^2 + R^2)^{3/2}} \] 這個公式適用於任何在z軸上的坐標點，應用這個公式我們來考慮下面兩個極端情況：
  1. 如果\(P\)點的位置非常靠近圓環的中心點，也就是\(z \ll R, \,\, z^2+R^2 \simeq R^2\)，在這個極限下我們可以忽略分母\(z^2\)的貢獻。可以看出在這個位置附近，電場的大小與場的位置與圓心的距離\(z\)成正比。
  2. 相對的，在另外一個極限下，場的位置非常遠離圓環的中心點(\(z \gg R, \,\, z^2+R^2 \simeq z^2\))，電荷圓環在遠處的電場貢獻就會類似於一個點電荷的電場--電場的大小與距離的平方成反比。
  3. 根據對稱性我們知道圓心處的電場必然是0，我們的公式也滿足這個條件。


直線電荷所產生的電場

在前面一個例子當中電荷呈現一維連續分佈，但排列的形狀是圓，在這一個例子當中我們來考慮同樣是一維的直線電荷分佈，如圖所示，整個直線的長度是\(L\)，直線上的總帶電量\(Q\)在直線上均勻分佈。我們要計算\(P\)點的電場，\(P\)點的位置在整個線段的垂直平分線上，與垂足的距離是\(R\)。我們一樣要從一小段的電荷貢獻的電場開始計算，從圖中我們可以寫下距離\(r,l\)與角度\(\theta\)之間的關係：\(R=r\cos \theta\), \( r= R \sec \theta\), \( l=R \tan \theta \) ，而\(\lambda\)是單位長度內所含的電量，稱呼為線電荷密度，\(\lambda=Q/L\)。因為\(P\)點的位置在線段的垂直平分線上，因此電場的貢獻是對稱的，所有\(y\)方向的分量會互相抵銷，最後一定只留下電場的\(x\)方向分量，因此我們只需保留電場的x方向分量。這一小段電荷\(dq=\lambda dl\)的電場貢獻為： \[dE=\dfrac{k dq}{r^2}=\dfrac{k \lambda dl}{R^2 \sec^2 \theta} \] \[=\dfrac{k \lambda R \sec^2 \theta d\theta}{R^2 \sec^2 \theta}=\dfrac{k \lambda d\theta }{R}\] 其中使用了微分關係：\(\dfrac{d \tan \theta}{d \theta}=\sec^2 \theta\)。如前所述，我們只需要留下\(x\)方向分量，也就是要將\(dE\)乘上\(\cos \theta\)。將整個帶電線積分就可以得到整體的貢獻： \[ E= E_x = \int dE_x = \int \cos \theta dE = \int_{- \theta_1}^{\theta_2} \cos \theta \dfrac{k \lambda d\theta }{R} = \dfrac{k \lambda}{R} [\sin \theta_2 + \sin \theta_1]=\dfrac{2 k \lambda}{R} \sin \theta . \] 根據對稱，\(\theta_1=\theta_2=\theta\)。有趣的結果是當直線的長度延伸到無窮長時\(L \rightarrow \infty ; \quad \theta=\dfrac{\pi}{2}\)，整個公式獲得的非常大的簡化： \[ E= \dfrac{2 k \lambda}{R} = \dfrac{\lambda}{2 \pi \varepsilon_0 R}. \] 電場的大小與距離\(R\)成一次方反比定律，任何一點的電場方向必然與帶電直線垂直向外輻射(\(Q \gt 0\))。

平面電荷所產生的電場

在上面的計算中我們已經利用對稱上的好處，計算出在帶電圓環中央軸上的電場，利用這個結果，下面我們來考慮一個帶電圓盤在中央軸上的電場。假設圓盤的半徑是\(R\)，整個圓盤的整體電量是\(Q\)，電荷均勻分佈在整個盤面，因此整個帶電圓盤的面電荷密度\(\sigma=\dfrac{Q}{\pi R^2}\)。首先我們將整個圓盤切割為許多同心的圓環，圓環的寬度是d\(r\)，針對半徑\(r\)的圓環我們已經知道在\(P\)點的電場為 \[dE=\dfrac{z\text{d}q}{4 \pi \varepsilon_0 (z^2+r^2)^{3/2}}\] 其中dq該圓環的整體帶電量\(\text{d}q=\sigma (2 \pi r \text{d}r) \)。對整體圓盤而言，只要把這樣的圓環積分就可以得到整體的電場，積分的細節如下： \[E=\int \text{d}E= \int_0^R \dfrac{z \text{d}q}{4 \pi \varepsilon_0 (z^2+r^2)^{3/2}} = \int_0^R \dfrac{2 \pi r z \sigma \text{d}r}{4 \pi \varepsilon_0 (z^2+r^2)^{3/2}} \]
\(E(z)=\dfrac{\sigma}{2\varepsilon_0} \left[ 1 - \dfrac{z}{\sqrt{z^2 + R^2}} \right] \)這個公式適用於任何在z軸上的坐標點，應用這個公式我們來考慮下面兩個極端情況：
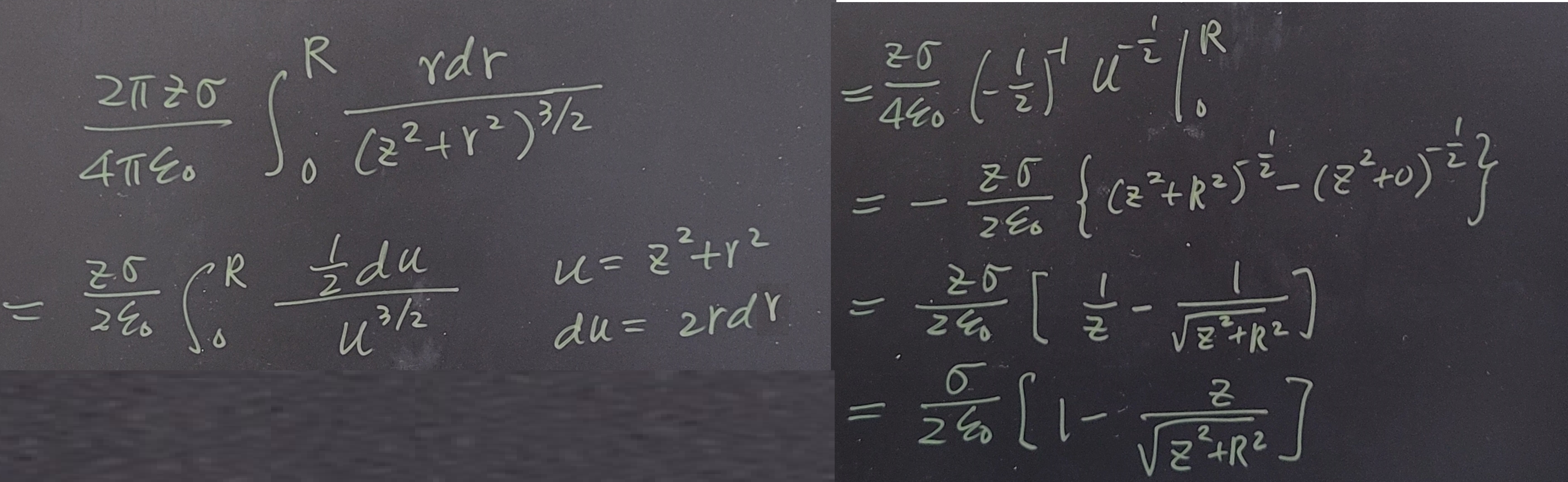
  1. 當\(P\)點非常接近圓心的時候(\(z \ll R\))，公式中分數的分子趨近0，分母卻是有限值\(R\)，因此整個分數趨近於0，則\(\left[ 1 - \dfrac{z}{\sqrt{z^2 + R^2}} \right] \simeq 1\)，也就是電場會是一個常數：\(E= \dfrac{\sigma}{2 \varepsilon_0}\)。這相當於一個無窮大的帶電平面板，電場的大小與\(z\)無關。換言之，當帶電平板的尺度非常大的時候，在板子上下兩側的電場是均勻的電場與距離無關。
  2. 當\(z \gg R\)，\(P\)點與圓心的距離遠大於面的尺度時， \[ \dfrac{z}{\sqrt{z^2+R^2}} = \dfrac{1}{\sqrt{1+(R/z)^2}} = [1+(R/z)^2]^{-1/2} \simeq [1 - 1/2 (R)^2] \] \[E \simeq \dfrac{\sigma}{2\varepsilon_0} \left[ 1 - [1 - 1/2 (R/z)^2] \right] = \dfrac{\sigma R^2}{4\varepsilon_0 z^2} = \dfrac{\sigma \pi R^2}{4 \pi \varepsilon_0 z^2} = \dfrac{Q}{4 \pi \varepsilon_0 z^2} \] 也就是當場點離帶電的平板非常遠，以至於整個圓盤可以視為一個點電荷的情況下，電場的行為當然又會恢復到點電荷的電場行為--電場的大小與距離的平方成反比。


各種電荷分佈的電場總結



電力線

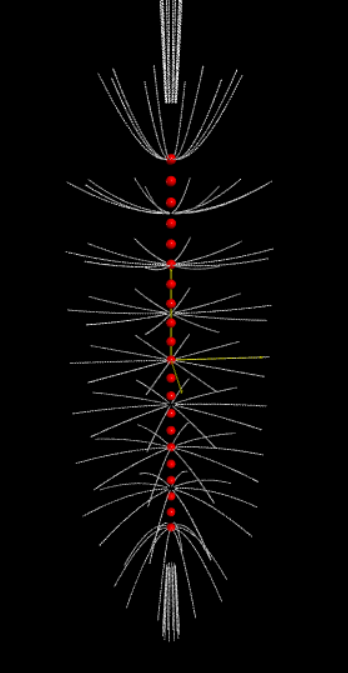
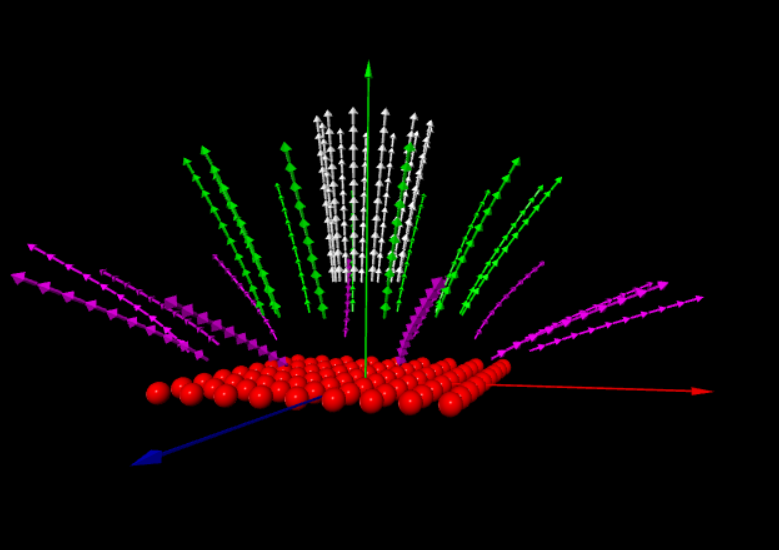
法拉第在19世紀引入了電場的概念，他認為帶電體周圍的空間充滿了力線。儘管我們不再對這些線（現在通常稱為電場線）賦予太多現實意義，但它們仍然提供了一種很好的方式來可視覺化電場中的模式。場線和電場矢量之間的關係是這樣的：(1)在任何一點，直線場線的方向或彎曲場線的切線方向給出了該點的方向，並且(2)繪製場線，以便在垂直於線的平面上測量的每單位面積的線數與電場的大小成正比。因此，電場E在場線靠近時較大，在場線較遠時較小分開。我們有以下規則：電場線從正電荷（它們起源的地方）指向負電荷（它們終止的地方）延伸。在下面的圖形中我們提供了三個電荷源所產生的電場，以及對應的電力線結構。它們分別是1.電偶極矩，2.排列成直線的電荷和3.排列成平面的電荷，並且我們提供了vpython語言的程式能夠計算並且畫圖。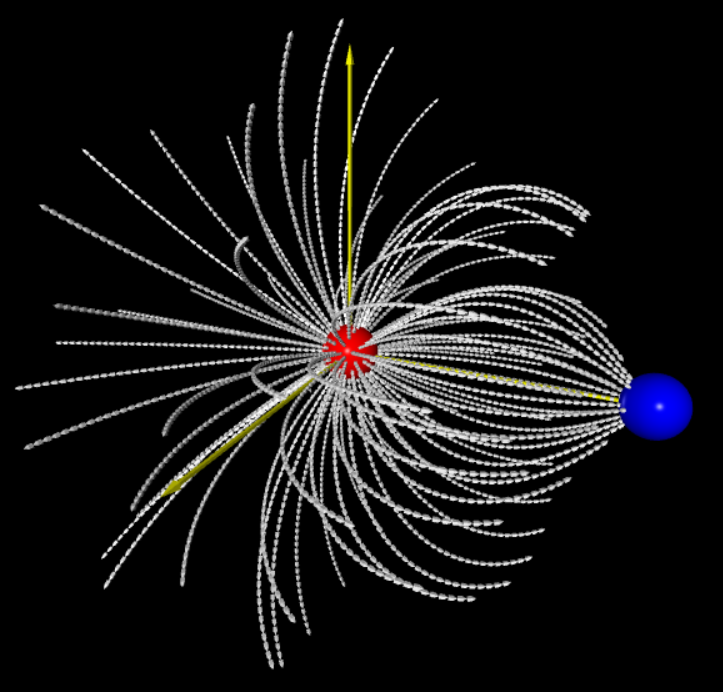




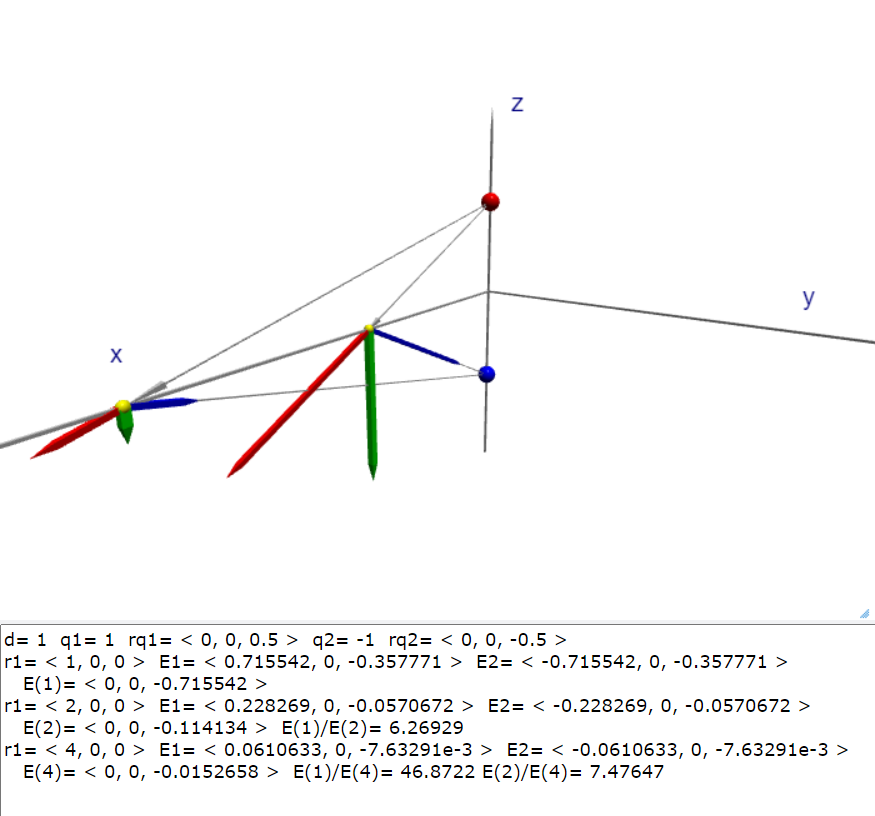
電偶極的電場計算

有一個電偶極放置在z軸上，正電荷和負電荷的位置分別是\( (0,0,d/2), \, \, (0,0,-d/2), \quad d=1\)，我們計算在x軸上兩個點位置\( (d,0,0) \, \,(2d,0,0)\)的電場，如圖形中所示。從這個計算我們得到重要的結論如下：
  • 正負電荷會給出兩個電場貢獻，但是因為對稱，最後這個電場會指向負z方向。
  • 場點在x軸的位置與原點的距離分別是1,2和4，當距離變化增大1倍，電場的大小幾乎衰減了1/8：
    \(E(1)/E(2)=6.27\)
    \(E(2)/E(4)=7.48 \simeq 8=2^3\)
    \(E(1)/E(4)=46.9 \simeq 64=4^3\)
    ，也就是與距離的三次方成反比，與我們在上面的計算是一致的。希望同學們可以從這個例子的計算當中體驗到用向量來計算電場的基本精神，如果你能夠善用vpython程式設計的話，那麼你可以用計算機來幫忙做計算，而且還可以畫出三維的立體圖。




點電荷在圓環中央軸進行簡諧運動

在上面的討論中我們已經討論過考慮過一個帶正電的圓環在中心軸上的電場如下： \[E(z)=\dfrac{qz}{4 \pi \varepsilon_0 (z^2+R^2)^{3/2}}\] 如果我們考慮\(z \ll R\)的情況下電場可以近似如下： \[ E(z) \simeq \dfrac{q}{4 \pi \varepsilon_0 R^3}z\] 如果考慮一個帶負電的電子初始的時候放置在+z-軸上方，電子將受到靜電力， \[ F(z)=-k z; \quad k=\frac{eq}{4 \pi \varepsilon_0 R^3} \] \(F\)大小與距離圓心的大小約略是正比關係，並且力量的方向始終指向圓心，所以這個力量就扮演了一個像彈性力一樣的恢復力，電子在這樣的靜電力作用下必然要進行簡諧運動。在下面的連結中我們使用vpython語言來模擬電子在帶電圓環中的簡諧運動，同學們可以驗證這個簡諧運動的週期，滿足了簡諧運動的週期公式： \[ T=2 \pi \sqrt{\dfrac{m}{k}} \]
glowscript:點電荷在圓環中央軸進行簡諧運動


範例-1：點電荷粒子的電場

The figure shows three particles with charges \(q_1=+2Q\), \(q_2=-2Q\), and \(q_3=-4Q\), each a distance \(d\) from the origin. What net electric field is produced at the origin?

該圖顯示了三個帶電荷的粒子 \(q_1=+2Q\)、\(q_2=-2Q\) 和 \(q_3=-4Q\)，每個粒子與原點的距離為 \(d\)。 原點產生的淨電場是多少？



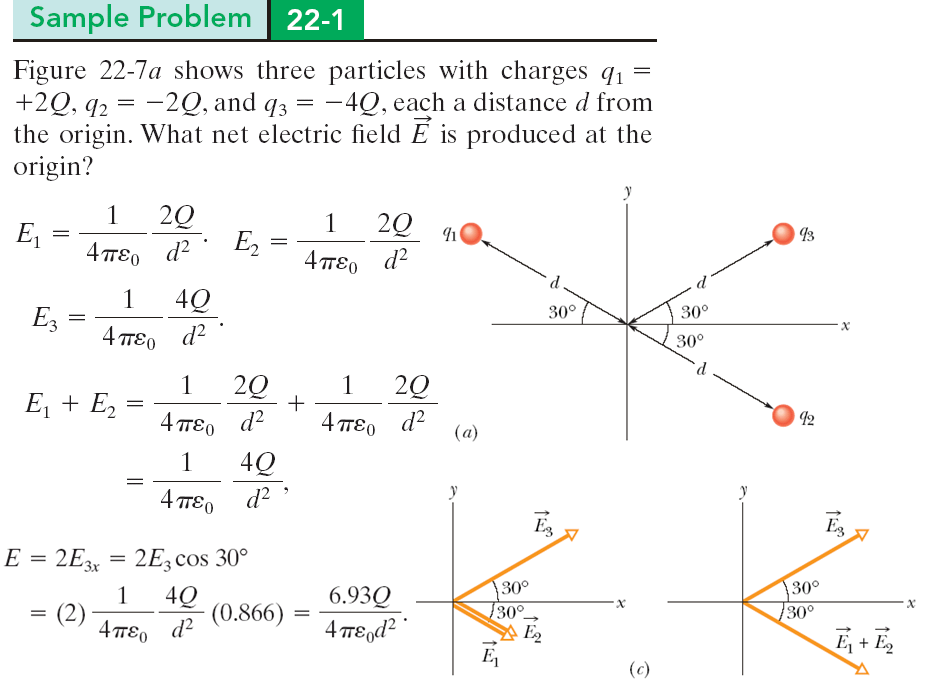
範例-2：電位差的計算(路徑積分)

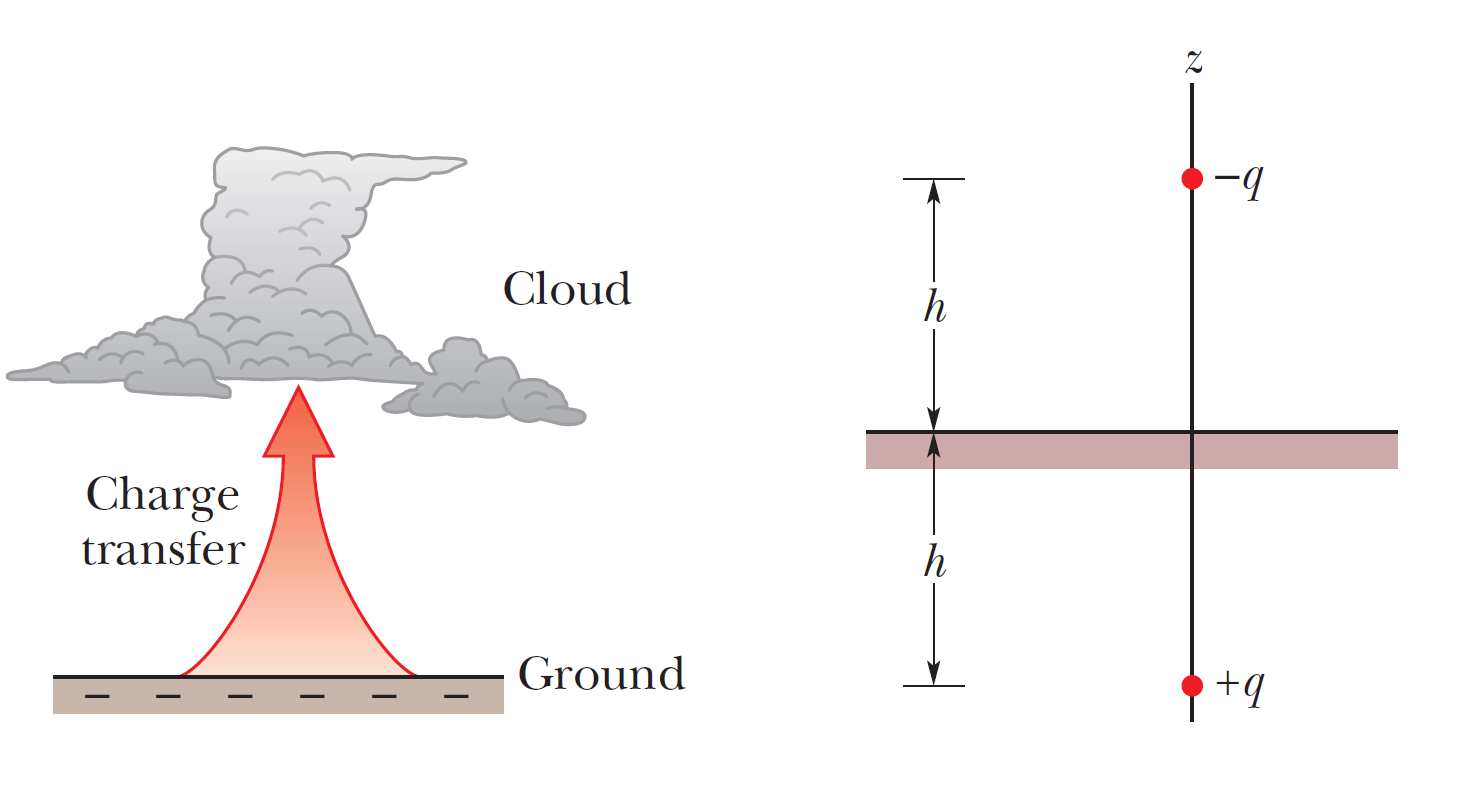
高空中出現的紅色精靈是發生在大雷暴上方的巨大閃光。數十年來，夜間飛行的飛行員一直看到它們，但它們是如此短暫和暗淡，以至於大多數飛行員認為它們只是幻覺。後來在 1990 年代，精靈被攝影機拍攝到。它們仍然不是很清楚，但被認為是在地面和暴風雲之間發生特別強大的閃電時產生的，特別是當閃電將大量的負電荷 \(-q\) 從地面轉移到雲底時。就在這樣的電荷轉移之後，地面具有復雜的正電荷分佈。但是，我們可以通過假設如圖所示，在地面與雲層之間存在鉛垂的電偶極子，在雲高度 \(h\) 處具有電荷 \(-q\) 並在地下深度\(h\)有電荷 \(+q\)。如果 \(q = 200\) C 和 \(h = 6.0\) km，在雲層上方 \(z_1 = 30 \) km 和高度 \(z_2 = 60\) 處偶極子電場的大小是多少）公里在平流層上方？

神秘的紅色精靈(許瑞榮，成功大學物理學系紅色精靈研究團隊)

電偶極子所產生的電場公式如下：

\(E=\dfrac{(2k)(q)(2h)}{z^3}\)

\(q=20 \, \text{C}, \quad h=6 \, \text{km}, \quad z=z_1,\,z_2\)

在坐標\(z_1=30 \times 10^3\)的電場\(E(z_1)=1.6 \times 10^3\) V/m，在坐標\(z_2=60 \times 10^3\)的電場\(E(z_2)=2.0 \times 10^2\) V/m。雖然高空\(z_2\)的電場比較小，但是在高空處的氣體密度更低，所以這樣的電場就已經達到氣體放電所需要的臨界電場\(E_c\)，因此使得\(z_2\)高空氣體放電。放電現象造成氣體原子發光，這就是紅色精靈的由來。
  • 左圖就是第一張由NASA拍攝到的紅色精靈相片。
  • 下圖左說明負電荷在閃電的過程中，從地面移動到雲層的下端。
  • 下圖右將電荷的分佈近似為一個電偶極矩，由電偶極矩所產生的電場說明紅色精靈發生的原因。


範例-3：帶電圓弧的電場

The figure (a) shows a plastic rod having a uniformly distributed charge \(-Q\). The rod has been bent in a 120° circular arc of radius \(r\). We place coordinate axes such that the axis of symmetry of the rod lies along the \(x\) axis and the origin is at the center of curvature \(P\) of the rod. In terms of \(Q\) and \(r\), what is the electric field due to the rod at point \(P\)?

圖 (a) 顯示了具有均勻分佈電荷 \(-Q\) 的塑料棒。 桿已彎曲成半徑為 \(r\) 的 120° 圓弧。 我們放置坐標軸，使桿的對稱軸位於 \(x\) 軸上，原點位於桿的曲率中心 \(P\)。 就 \(Q\) 和 \(r\) 而言，在點 \(P\) 處由棒產生的電場是多少？



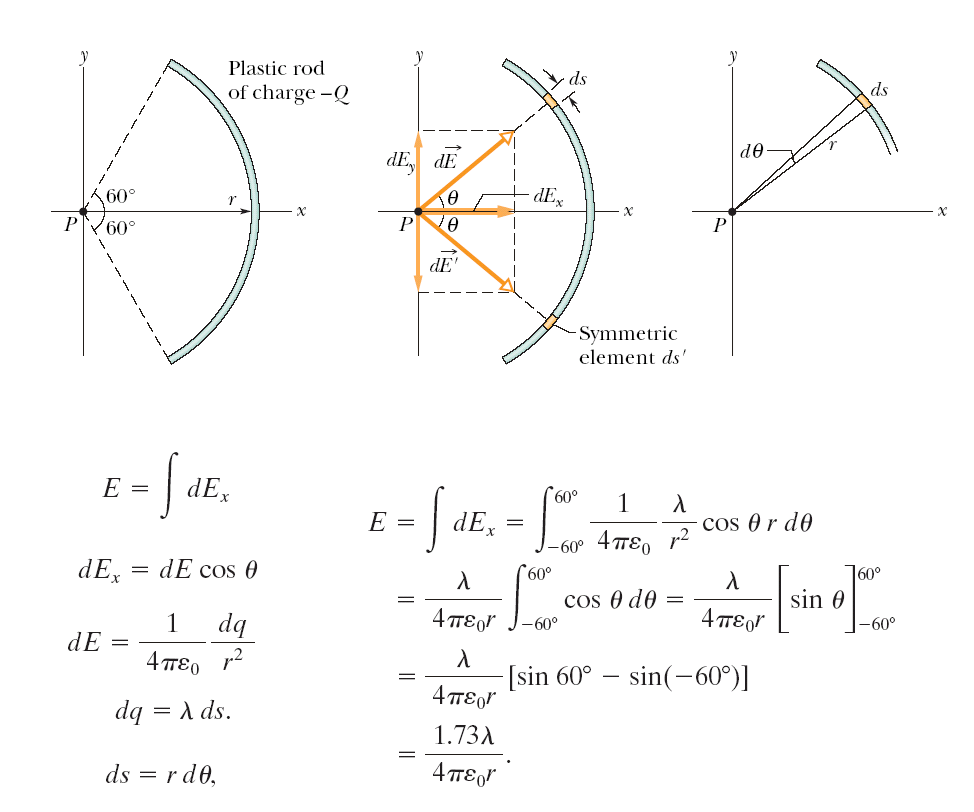
範例-4：噴墨式印表機

The figure shows the deflecting plates of an ink-jet printer, with superimposed coordinate axes. An ink drop with a mass \(m\) of \(1.3 \times 10^{-10}\) kg and a negative charge of magnitude \(Q =-1.5 \times 10^{-13}\) C enters the region between the plates, initially moving along the \(x\) axis with speed \(v_x = 18\) m/s. The length \(L\) of each plate is 1.6 cm. The plates are charged and thus produce an electric field at all points between them. Assume that field \(E\) is downward directed, is uniform, and has a magnitude of \(1.4 \times 10^6\) N/C. What is the vertical deflection of the drop at the far edge of the plates? (The gravitational force on the drop is small relative to the electrostatic force acting on the drop and can be neglected.) 該圖顯示了噴墨式印表機的偏轉板，坐標軸如圖所示。有一個質量為 \(m =1.3 \times 10^{-10}\) kg和帶電量為為\(Q =-1.5 \times 10^{-13}\) C 的負電荷的墨滴進入兩板之間的區域，最初沿 \(x\) 軸以速度 \(v_x = 18\) m/s 移動。 每個板的長度 \(L\) 為 1.6 cm。 兩板帶異性電，因此在它們之間的所有點處產生電場。假設電場\(\vec{E}\)的方向向下並且均勻，其大小 \(E=1.4 \times 10^6\) N/C 。計算電板遠端的液滴垂直的偏移輛？（液滴上的重力相對於作用在液滴上的靜電力極小，可忽略不計。）



glowscript:噴墨式印表機(glowscript)




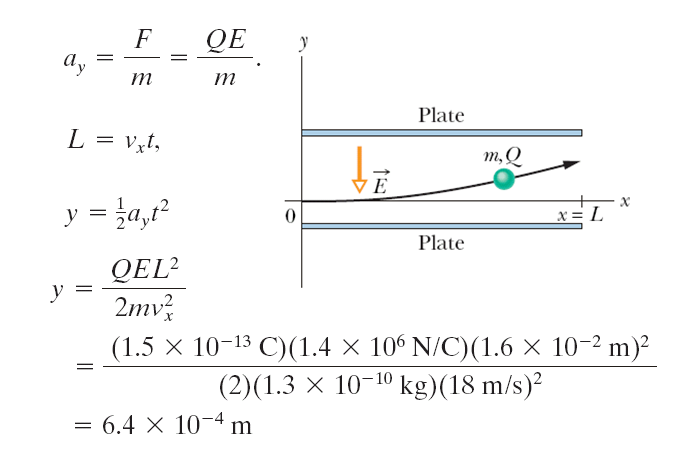
授課教師
陳永忠 ycchen@thu.edu.tw