電磁感應

在上一單元中，我們討論了電流產生磁場的事實。這一事實讓發現這種效應的科學家感到驚訝。或許更令人驚訝的是反向效應的發現：磁場可以產生可以驅動電流的電場。磁場與其產生（感應）的電場之間的這種聯繫現在稱為法拉第感應定律。邁克爾法拉第和其他科學家的觀察導致這一定律起初只是基礎科學，有趣的是它們揭示了我們宇宙如何運作的另一個方面。然而，今天，該基礎科學的應用幾乎無處不在。例如，感應是電吉他的基礎，它徹底改變了早期搖滾，今天仍然驅動重金屬和朋克。它也是為城市和交通線路供電的發電機的基礎。儘管用於廚房的感應爐尚未受到專業廚師或業餘廚師的歡迎，但大型感應爐在必須快速熔化大量金屬的鑄造廠中很常見。在我們討論電吉他這樣的應用之前，我們必須檢查兩個關於法拉第感應定律的簡單實驗。





法拉第感應定律

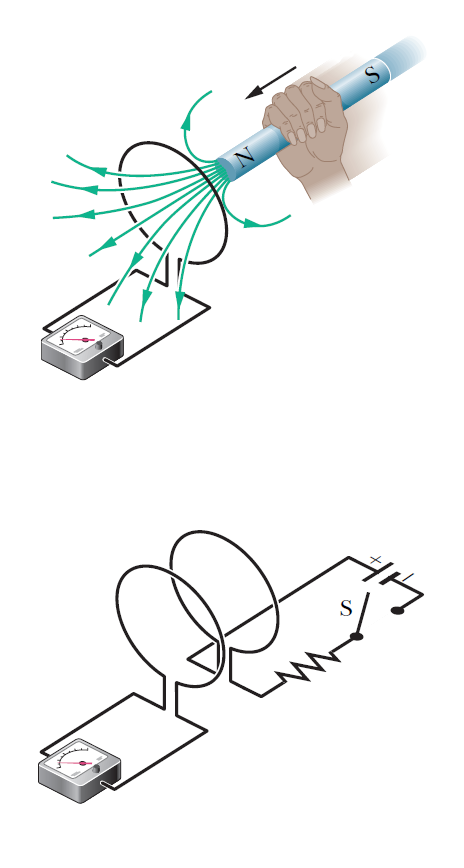為了讓我們能夠更清楚感應電動勢產生的現象，讓我們先觀察兩個簡單的實驗，為我們討論法拉第感應定律做準備。
這些實驗中的感應電動勢和感應電流顯然是在某些東西發生變化時引起的。但那個“東西”是什麼？法拉第意識到，通過改變通過環路的磁場量，可以在迴路中產生感應電動勢和電流，就像在我們上述的兩個實驗中一樣。 他進一步意識到，“磁場量”可以通過穿過迴路的磁場線來視覺化。法拉第感應定律可用實驗表述如下：

當通過迴路的磁力線數量發生變化時，迴路中感應出一個電動勢。

通過環路的實際磁力線數量無關緊要；感應電動勢和感應電流的值取決於磁通量的變化率。法拉第定律並未解釋為什麼在這兩個實驗中都會產生電流和電動勢，只是對感應電動勢產生的現象做一個歸納性的陳述。

磁通量與法拉第定律

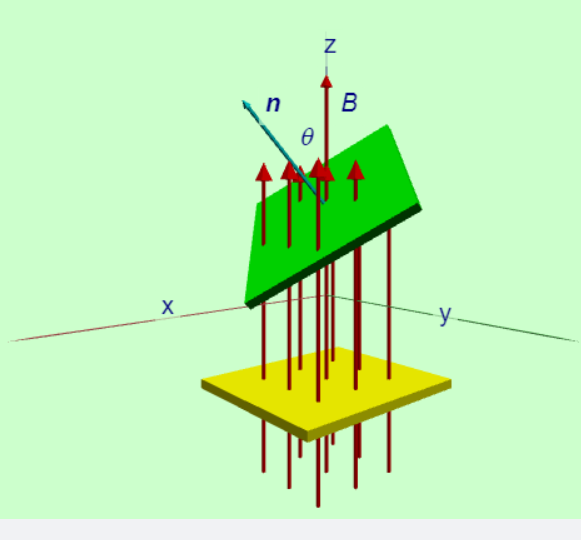為了使法拉第定律起作用，我們需要一種方法來計算通過環路的磁場量。 在第3單元中，在類似的情況下，我們需要計算通過表面的電場量，並且利用封閉曲面的電通量建立其與被包覆的電荷之間的關係。我們定義電通量 \(\Phi_E=\int \vec{E} \cdot d\vec{s}\)。 已知在空間中有一個磁場向量分佈在空間中的每一個位置，考慮在這個空間中有一個曲面\(S\)，這個曲面上各處的面積單元向量\(d\vec{s}\)由法線向量\(\hat{n}\)決定該面積單元的方向，\(d\vec{s}=ds \hat{n}\)。磁場穿越過每一個面積單元的角度\(\theta\)可能各自不同，我們可以對每一個面積單元計算磁場與面積單元的法線向量的內積來定義該面積單元的磁通量貢獻(\(d\Phi=\vec{B} \cdot d\vec{s}\))，將所有面積單元的磁通量貢獻積分之後，就可以得到整體曲面的磁通量。磁通量的定義： \[\Phi_B = \int_S d\Phi= \int_S \vec{B} \cdot d\vec{s}. \] 如右圖所呈現的，如果面的法線方向和磁場的方向相同那麼磁通量就是\(\Phi_B= BA\)。如果面與磁場的方向有一個夾角\(\theta\)，那麼磁通量\(\Phi_B=BA \cos \theta\)。

考慮一個面\(S\)，其周圍是一個封閉的曲線\(C\)，如果這個曲線就是一個導線迴路，法拉第的電磁感應定律告訴我們，如果這個面的磁通量\(\Phi_B\)隨著時間變化，那麼在這一個面的邊緣上的導線迴路\(C\)中將會產生一個感應電動勢\(\mathcal{E}\)，其關係如下： \[\mathcal{E}=-\dfrac{d \Phi_B(t)}{dt} =- \dfrac{d}{dt} \int_S d\Phi_B = -\dfrac{d}{dt} \int_S \vec{B} \cdot d\vec{s}. \] 在公式中我們看見感應電動勢有一個負號，這是依據上面的實驗結果而加入的。因為感應電流流動的方向總是與磁通量改變的方向相反：當磁鐵棒的N極向迴路靠近的時候，磁通量將要增加，這時在迴路線圈中的感應電流方向，會產生一個反方向的磁通量，阻擋磁鐵棒的磁通量增加。相對的當磁鐵棒的N極離開迴路線圈的時候，迴路磁通量逐漸減小，此時在迴路線圈中感應出的電流會倒過頭來，產生一個磁場要增加迴圈中的磁通量，也就是要阻擋因N極的離開所造成的磁通量下降。所以整體而言，感應電動勢的方向始終是為了要維持住迴路線圈中的磁通量，不讓磁通量發生改變。事實上這個負號是由冷次(Lenz)首先提出，因此也稱為冷次定律。若迴路線圈的圈數不只是1，而是有\(N\)個迴路構成，那麼上述的公式中乘以倍數\(N\)： \[\mathcal{E}=-N\dfrac{d \Phi_B(t)}{dt}. \]

感應和能量轉移

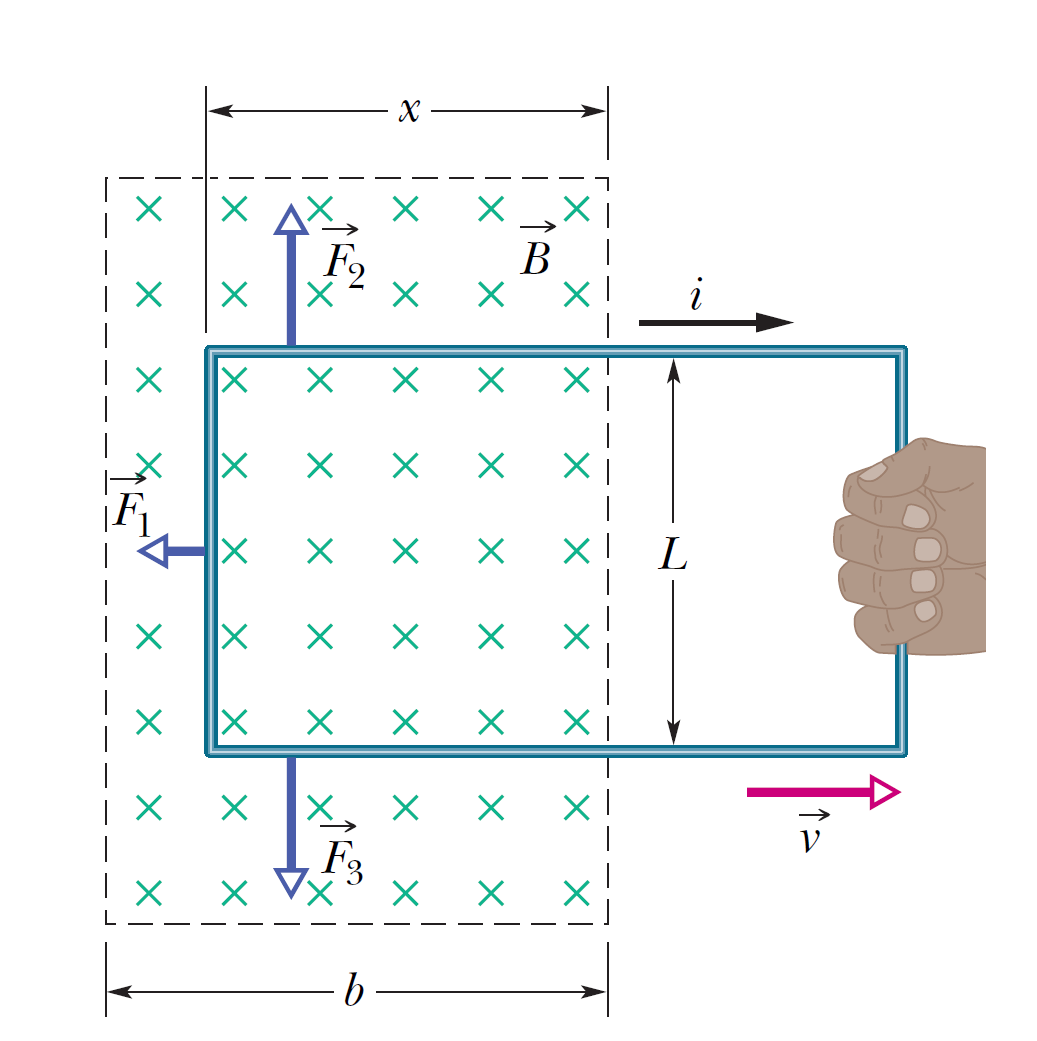如右圖所呈現的，有一個均勻磁場的方向垂直穿入紙面，在磁場中我們有一個長方形的導體迴路，如果我們要將這個迴路從磁場的區域中拉出，線圈要離開磁場會造成線圈中的磁通量減少，根據上一節所討論的冷次定律，我們知道導體迴路中會產生一個感應電流阻擋磁通量的減少，因此如果我們要讓這個導體迴路持續運動離開磁場，必須對這個導體迴路施加一個往外拉的力量。假設我們對這個導體施加了一個適當的力\(F\)，讓導體迴路可以等速度\(v\)的向右方運動離開磁場，那麼根據功率的定義，我們知道這個外力對線圈的功率為 \[P=Fv\] 為了要計算外力的大小，我們對整個問題定下一個座標系統：假設往右邊的方向是+x的方向，向上的方向是+y的方向，線圈在y方向的長度是\(L\)，速度是在+x方向。根據冷次定律感應電流的流向是順時針方向，感應電流來自於感應電動勢。根據法拉第定律為了計算感應電動勢，我們必須要計算磁通量對時間的微分。在任何時間磁場垂直穿過導線迴路，因此磁通量可磁通量可寫成： \[\Phi(t)=BLx(t)\] \[\mathcal{E}=-\dfrac{d \Phi(t)}{dt}=-\dfrac{d BLx(t)}{dt}=-BL-\dfrac{dx(t)}{dt}=-BLv\] 假設長方形的導體迴路的等效電阻為\(R\)，因此我們可以利用歐姆定律\(\mathcal{E}=iR\)算出感應電流的大小： \[i=\dfrac{\mathcal{E}}{R}=\dfrac{BLv}{R}\] 假如速度是常數這個力量也是常數，也就是以一個定力向右拉電流迴路，就可產生等速度的運動。力和速度的關係可以再進一步推導出來。因為電流在磁場中受到磁力的作用，在磁場中的三個電流部分所受磁力的方向分別如圖所標示。向\(\pm x\)流動的電流所受的磁力相等，但是方向相反，因此這兩個力量互相抵銷。最左側的電流受到的磁力向(-x)與向右的拉力平衡，使導線迴路維持等速度運動，因此我們計算出拉力的大小： \[F=iLB=\dfrac{BLv}{R} LB=\dfrac{B^2 L^2 v}{R}\] 因此外力對線圈的功率\(P\)： \[P=Fv=\dfrac{BLv}{R} LB=\dfrac{B^2 L^2 v^2}{R}\] 線圈中的電流發熱的功率\(P_R\)： \[P_R=i^2 R=\dfrac{\mathcal{E}}{R}=\dfrac{B^2 L^2 v^2}{R^2} R=\dfrac{B^2 L^2 v^2}R=P\] 線圈中的電流發熱的功率等於外力對線圈的功率，滿足能量守恆的條件。換言之，外力對線圈迴路所做的功全部轉換為電流所發出的歐姆熱。

感應電場

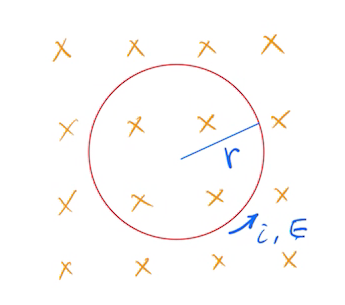我們將一個半徑為\(r\)的銅環置於一個均勻的外部磁場中，如右圖所示。假設我們以穩定的方式增加磁場的強度，例如以穩定的方式增加線圈中的電流，就可以穩定的增加磁場的大小。然後通過環的磁通量將以穩定的速率變化，並且根據法拉第定律銅環中將有感應電動勢及感應電流出現。根據冷次定律，我們可以推斷出感應電流的方向為逆時針方向。相對的如果我們穩定的減少線圈中的電流，就會穩定的減少磁場，進而減少通過圓環的磁通量，根據冷次定律就會在銅環當中產生順時針方向的電流。

如果銅環中有電流，則沿環必須存在電場，因為需要電場來完成移動傳導電子的工作。而且，電場一定是由變化的磁通量產生的。這個感應電場與靜電荷產生的電場一樣真實；任何一個場都會對帶電粒子 \(q_0\) 施加一個力。根據這些推理我們可以重新將法拉第定律陳述如下：

時變的磁場會產生電場。

在第四個單元我們定義電位差的時候，已經理解空間中兩點的電位差，可以透過選擇一條路徑，對電場在這一條路徑上進行路徑積分，可得到這兩點的電位差。但是對靜電場而言，庫倫力是一個保守力，這兩點的電位差的大小與所選取的路徑無關。更進一步，對於保守場中做封閉路徑的積分，必然得到電位差等於0，這是靜電場作為一個保守場，必然具備的特性。對感應電場而言我們得到一個截然不同的結果，感應電場在一個封閉的路徑的積分，我們會得到非零的電位差，也就是由於磁通量對時間的變化而產生的感應電動勢。所以我們知道我們上面所提到的感應電場，顯然和我們在之前所談到的靜電場具有截然不同的性質，感應電場不是一個保守場，因此在一個封閉的路徑中，對感應電場作路徑積分會得到有限值，這個數值就是感應電動勢，其公式如下： \[\oint_C \vec{E}_{ind} \cdot d\vec{s} = \mathcal{E} = - \dfrac{d\Phi_B}{dt}.\] 所以在上面的公式中我們對感應電場作路徑積分所得到的結果，已經不具有電位差的意義，電場的路徑積分對應到電位差的結論，只對靜電場是有意義的 ，對電磁感應產生的電場沒有意義的。

渦電流

若將一個矩形的線圈以初速度垂直射入磁場中，當線圈的一部分進入磁場後線圈上便會出現感應電流，依冷次定律此線圈受一個排斥力的作用因而被減速。若進入磁場的不是一個矩形線圈，而是一個薄的金屬板，當有部分進入磁場時，在金屬板的內部及表面也會出現感應電流，這種感應電流形狀像是水中的渦流，所以稱呼為渦電流。此金屬板在進入磁場的過程中會受到排斥力而減速，這種減速作用被應用作為捷運電聯車的煞車系統。在電聯車的輪子附近裝有電磁鐵，要煞車時通以大電流使電磁鐵產生磁場，在鋼軌上感應出渦電流，進而產生煞車的作用。這種煞車作用和車速有關，若起初的速度越快，感應生成的渦電流就越大，排斥力也越大，煞車的力量也越強。煞車開始後車速減小，渦電流跟著變小，煞車力也隨之變小，因此這種被稱為渦電流煞車的設計，可提供平穩的煞車。導體進出磁場固然會感應出渦電流，磁場隨時間改變靜止的導體上，也會產生渦電流。這種波電流會出現在變壓器、馬達和發電機的軟鐵蕊上。渦電流的壞處之一是會產生熱而消耗能源，為了要降低渦電流的熱效應，通常將鐵蕊分成多層互相絕緣良好的部分，軟鐵蕊上的感應電動勢大小和和電流所能涵蓋的面積有關，因此層狀的鐵蕊可有效減小渦電流的環路大小，使渦電流變小。導體上的渦電流雖然會再變壓器之類的設備上產生熱的不良後果，但也有正面的應用，例如電磁爐及高溫感應爐，就是再利用波電流所產生的熱效應，來加熱食物或製備樣品。

電感器和電感

假如我們將一個圓形線圈接至一個端電壓為\(V\)的直流電池，如圖所示。當按下開關\(S\)接通電路時，線圈上的電流並不會突然間有零升至\(V/R\)，這乃是因為當線圈上的電流開始由零增加時，此電流所產生的磁場穿過線圈本身的磁通量也隨時間增加，這種隨時間增加的磁通量，促成線圈上出現一個會抵制磁通量改變的感應電動勢，這個自我感應的電動勢，在電流增加的過程中其極性相反於外加的電動勢，因此線圈上的電流是漸次增加至飽和值\(V/R\)，而非突然增加至\(V/R\)。這種在導電線圈上自我的電磁感應現象，稱為自感應，自感應所產生的電動勢是一種反電動勢(back emf)，顯然正比於線圈上的電流的時間改變率， 當線圈是由N個線圈導線組成，而且通過每圈導線的磁通量相等，自感的感應電動勢可寫成 \[\mathcal{E}=-N\dfrac{d\Phi_B}{dt}=-L\dfrac{di}{dt}\] 上式中\(i\)為線圈上的電流，\(\Phi_B\)為電流所產生的磁場穿過一圈導線的磁通量，比例常數\(L\)稱為此線圈的自感(self inductance)。因此自感的定義如下： \[L=\dfrac{N \Phi_B}{i}\] 我們可用上式定義與測量自感。自感的單位是亨利(H)。在上面我們所討論的長方形線圈在磁場中的運動時，我們只考慮了外加磁場通過長方形線圈的磁通量隨時間的變化，事實上感應電流所產生的磁場也穿過長方形線圈，這部分電流對磁通量也是有所貢獻，但是我們假設感應電流所產生的磁場遠遠小於外加的磁場，因此其貢獻忽略不計。

考慮一個細長的螺線管，其半徑為\(a\)，長度為\(l\)，單位長度有\(n\)圈，計算此螺線管的自感。當此線圈上載有穩定的電流\(i\)時，線圈內的均勻磁場及其方向平行於線圈的長軸，而其量值為 \[磁場：B=\mu_0 n i\] \[磁通量：\Phi_B=B (\pi a^2)=\mu_0 n i (\pi a^2) =(\mu_0 n \pi a^2) i\] \[總磁通量：N=nl; \quad N\Phi_B=(\mu_0 n^2 \pi a^2 l) i\] \[自感：L=\mu_0 n^2 \pi a^2 l\]

RL 電路

考慮一個自感為\(L\)的線圈與電阻\(R\)，以及一個電動勢為\(\mathcal{E}\)的直流電池所構成的電路，如圖所示。假設電池的內電阻及感應線圈的電阻均遠小於\(R\)，可忽略不計。並且假設開關\(S\)按下前，電路上的電流為0，當開關\(S\)在\(t=0\)按下時，電路接通電流開始增加，同時在感應線圈上出現一個感應電動勢\(\mathcal{E}_L\)對抗電池的電動勢\(\mathcal{E}\)，因為\(\mathcal{E}_L\)對抗\(\mathcal{E}\)，\(\mathcal{E}\)又稱為反電動勢： \[\mathcal{E}_L=-L\dfrac{di}{dt}\] 應用迴路定理可得： \[\mathcal{E}-iR-L\dfrac{di}{dt}=0\] 又可以改寫成 \[\dfrac{di}{dt}+\dfrac{R}{L}i=\dfrac{\mathcal{E}}{L}\] 成要解這個微分方程式，可令(做變數變換) \[u=\dfrac{\mathcal{E}}{R}-i\] \[\dfrac{du}{dt}=-\dfrac{di}{dt}\] 上面的迴路定理方程式 \[\dfrac{du}{u}=-\dfrac{R}{L}dt\] 直接積分可以得到 \[\int_{u_0}^{u} \dfrac{du}{u}=-\dfrac{R}{L} \int_0^t dt\] \[\ln(\dfrac{u}{u_0})=-\dfrac{Rt}{L} \] \[ u(t)=u_0 e^{-\frac{Rt}{L}}\] \[i(t)=\dfrac{\mathcal{E}}{R} - i_0 e^{-\frac{Rt}{L}}\] 電流是時間的函數。已知的初始條件：\(i(t=0)=0, \Rrightarrow i_0=\dfrac{\mathcal{E}}{R}\)。 \[i(t)=\dfrac{\mathcal{E}}{R} \left[ 1 - e^{-\frac{Rt}{L}} \right] \] \(\tau\)具有時間的因次，故稱為RL串聯電路的鬆弛時間(relaxation time)或時間常數(time constant)。電流隨時間的變化圖形如右圖所示，當時間遠大於時間常數\(t \gg \tau\)，電流趨近於其飽和值\(\frac{\mathcal{E}}{R}\)。當\(t=\tau\)， \[i(\tau)=\dfrac{\mathcal{E}}{R} (1 - e^{-1}) \simeq 0.63 \dfrac{\mathcal{E}}{R} \] 此時的電流達到飽和值的0.63倍。 依據電感的定義我們知道感應電動勢正比於電流對時間的微分，比例常數就是電感：\(\mathcal{E}_L=-L\dfrac{di}{dt}\)。所以我們對電流的時間函數微分 \[\dfrac{di}{dt}=\dfrac{R}{L}\dfrac{\mathcal{E}}{R} e^{-\frac{Rt}{L}} = \dfrac{\mathcal{E}}{L} e^{-\frac{Rt}{L}} \] 得到微分在T等於臨時有最大值所以這個時候感應線圈上的反電動勢最大而隨著時間的增長電流漸漸增加微分也漸漸變小反電動勢也隨之變小最後電流趨近於穩定值微分則趨近於零感應線圈形同短路狀態 T等於0的時候電流對時間的微分有最大值當然也就代表此時感應線圈上的反電動勢最大而隨著時間的增長電流逐漸增加電流對時間的微分也逐漸變小反電動勢隨之減小最後電流會趨近於穩定值也就是感應線圈如同短路

儲存在磁場中的能量

一個載有電流的線圈擁有能量，電流會產生磁場所以電流的能量稱為磁場能量，簡稱為磁能。一個電荷系統的電能定義為在電荷系統的建立過程中，外力對抗電荷間的庫侖力，所必須做的功。電流的磁磁能又如何定義呢？這個問題可以從上一節中的RL電路獲得答案。從迴路定理我們得到下列公式： \[\dfrac{di}{dt}+\dfrac{R}{L}i=\dfrac{\mathcal{E}}{L}\] \[ \mathcal{E}=iR + L \dfrac{di}{dt}\] 在這個公司的兩端兩邊都乘以電流i可以得到\(i \mathcal{E}\)=電池在單位時間內所提供的能量，\(i^2 R\)=電阻\(R\)在單位時間內所消耗的熱量，因此從能量守恆考量，最後一項\(L i \dfrac{di}{dt}\)代表線圈的磁能在單位時間內的增加速率。如果以\(U_B\)表示磁能，那麼上一個公式可以改寫成 \[ \dfrac{d U_B}{dt}=L i \dfrac{di}{dt}=\dfrac{d(1/2 L i^2)}{dt}\] 初始條件是\(t=0, \quad i=0, \quad U_B=0\)，如果將上面的公式積分可以得到線圈當中的電流為\(i\)的時候其所儲存的磁能為： \[U_B=1/2 L i^2\] 電荷系統的電能可視為儲存在所建立的電場內， \[電能密度=u_E=1/2 \varepsilon_0 E^2\] 同理，電流系統的磁能也可視為儲存在所建立的磁場中。那我們將以承載電流的螺線管為例，導出單位體積的磁場所儲存的磁能。

螺線管的半徑為\(a\)，長度為\(l\)，單位長度的圈數密度是\(n\)。上面我們已經得到電感的公式如下 \[L=\mu_0 n^2 \pi a^2 l \] 當此線圈承載電流\(i\)時，線圈內的磁場值為\(B=\mu_0 n i\)，所以螺線管內所儲存的磁能為 \[U_B=1/2 L i^2 = 1/2 (\mu_0 n^2 \pi a^2) (i^2)= 1/2 (\mu_0 n^2 \pi a^2) (\dfrac{B}{\mu_0 n}=\dfrac{B^2}{2 \mu_0} (pi a^2 l) \] 上面公式中\(\pi a^2 l\)是螺線管所包圍的體積，所以螺線管內的磁能密度可寫為 \[u_B=1/2 L i^2 = \dfrac{B^2}{2 \mu_0} \] 在電學的討論中我們已經知道電能密度正比於電場的平方，上面的推導得到類似的結果，也就是磁能的密度正比於磁場的平方。這個公式雖然是從螺線管這個例子所導出的，但是適用於任意的電流系統，因此一個電流系統中的磁能可以表示為 \[U_B = \int u_B dV= \int \dfrac{B^2}{2 \mu_0} dV \] 利用磁能我們也可以提供另一個計算電流線圈自感的方法： 下面我們來考慮一個同軸電纜線的磁能問題。假設我們有一個同軸電纜線，有一個半徑\(a\)的實心導線，外導體為一個厚度可忽略不計的一個圓柱殼，半徑為\(b\)，如圖所示。當內外導體分別載有電流\(i\)和\)\)時，求(a)單位長度內所儲存的磁能，(b)單位長度的自感。當同軸電纜所通的電流是直流電流時，內導體的電流密度可視為均勻，而比大於R範圍內磁力線是圓心位於圓柱軸上的圓磁場的量值可應用安培定律得到R大於b10磁場為零當R小於20 B等於當R在愛與秘之間的時候比等於磁場能量儲存於導體之內以及內外兩導體之間單位長度的內導體所儲存的磁能為內外導體之間單位長度所儲存的磁能為從這兩個公式我們可以得到單位長度的同軸電纜線所儲存的磁能為根據電感的詞能定義我們得到單位長度的電感如下



授課教師
陳永忠 ycchen@thu.edu.tw