波函數的基本性質
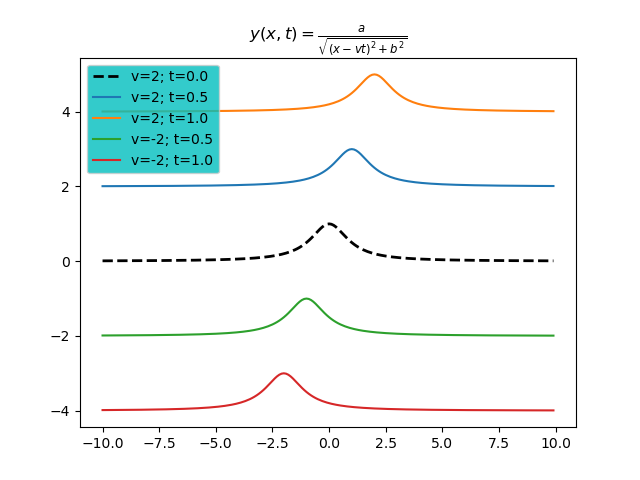
#利用python和matplotlib繪製波函數 import math import numpy as np import matplotlib import matplotlib.pyplot as plt sqrt=math.sqrt; N=10 a=1; b=1; v=2 x=np.arange(-10,10,0.1) for j in range(3): t=0.5*j y=a/((x-v*t)**2+b**2)+j*2 s='v=2; t='+str(round(t,1)) if(j==0): plt.plot(x,y,'k--',lw=2,label=s) else: plt.plot(x,y,label=s) for j in range(1,3): t=0.5*j y=a/((x+v*t)**2+b**2)-j*2 s='v=-2; t='+str(round(t,1)) plt.plot(x,y,label=s) plt.title(r"$y(x,t)=\frac{a}{\sqrt{(x-vt)^2+b^2}}$") plt.legend(loc='upper left',facecolor='c') plt.savefig('Lorentzian-wave-v.png') print('done')
簡諧運動的微分方程
在我們要進行波動方程式的介紹之前我們現在回頭看一下前一個單元的簡諧運動。在簡諧運動的問題當中我們要尋找簡諧運動物體的位置對時間所必須滿足的方程式,這樣的方程式會是一個微分方程式,方程式的解就是描述物體在進行簡諧運動時位置對時間的函數關係,\(x(t)\)。因為這是一個週期性的運動,因此具有這樣性質的最基本函數就是三角函數: \[x(t)=A \cos(\omega t + \phi) .\] 我們也知道三角函數微分的關係:\(\cos\)函數微分一次會得到\(-\sin\)函數,再微分一次又會回到\(-\cos\)函數,因此我們知道\(x(t)=A \cos(\omega t + \phi)\) 這個週期性函數要滿足以下的微分方程式: \[\dfrac{d^2 x}{dt^2}=-\omega^2 x(t).\] 以上的討論是完全從數學上來分析三角函數作為一個週期性函數必須滿足的微分方程式。雖然是針對三角函數所得到的微分方程式,如果我們大膽的推測所有的週期性運動應該都要滿足這一個微分方程式,那麼這個微分方程式本身應該有更高層次的普遍性。事實上我們知道這個微分關係其實就是牛頓的運動學第二定律,力與加速度之間的關係: \[f=ma\] 如果考慮彈簧的簡諧運動系統,這裡的力是虎克定律當中的彈性力\(f=-kx\),並且已知加速度\(a\)是位置\(x(t)\)對時間的二階微分:\[a=\dfrac{d^2 x}{dt^2}=\dfrac{f}{m}=-\dfrac{k}{m} x.\] 比較上面這兩個微分方程式我們就可以把位置的週期性函數當中的參數與實際彈簧系統的物理量相對應:例如函數中的\(A\)就是簡諧運動物體的最大擺動幅度,這個最大擺動幅度與簡諧運動的力學能有關;簡諧運動的角頻率\(\omega\)就與彈性係數\(k\)和物體的質量\(m\)有關,\(\omega^2=\dfrac{k}{m}; \,\, \omega=\sqrt{\dfrac{k}{m}}\)。因此如果結合了物理學的基本定律,數學上的函數當中的各個參數就有了物理系統的對應關係,因此數學不只是數學,而是對應了一個真實物理現象中的物理系統。波動方程式
讓我們再回到波的問題,我們一樣從數學上知道波函數\(y(x,t)\)必須滿足特定的函數關係,波函數是一個雙變數的函數同時具有空間和時間變數,相對的,簡諧運動中的位置只是單純的時間函數\(x(t)\),其所對應的方程式只包含對時間微分的方程式,我們稱為常微分方程式。對於波函數而言,我們要尋找的方程式可能同時包含對空間和對時間的微分,這時候我們會用到偏微分的量,而這些偏微分量所要滿足的方程式就稱為偏微分方程式。同學們可以很快的驗證,若 \[y(x,t)=\dfrac{a}{(x-vt)^2+b^2}=a[(x-vt)^2+b^2]^{-1}\] 滿足在上述的波方程式 \[\dfrac{\partial^2 y}{\partial x^2}=\dfrac{1}{v^2}\dfrac{\partial^2 y}{\partial t^2}\] 我們可以透過對\(y(x,t)\)做偏微分運算: \[\dfrac{\partial y}{\partial x}=-a[(x-vt)^2+b^2]^{-2}(2(x-vt))\] \[\dfrac{\partial^2 y}{\partial x^2}=... \] \[\dfrac{\partial y}{\partial t}=-a[(x-vt)^2+b^2]^{-2}(2(x-vt))(-v)\] \[\dfrac{\partial^2 y}{\partial t^2}=... \] 可以證明這個波函數會滿足波方程式。 我們也可以嘗試驗證一個連續波,例如三角函數波: \[y(x,t)=y_m \sin(kx - \omega t) \] 經過對時間和空間的偏微分之後,可以驗證這個函數一樣滿足波方程式的微分關係: \[\dfrac{\partial y}{\partial x}=k y_m \cos(kx-\omega t)\] \[\dfrac{\partial^2 y}{\partial x^2}=-k^2 y_m \sin(kx-\omega t) \] \[\dfrac{\partial y}{\partial t}=-\omega y_m \cos(kx-\omega t)\] \[\dfrac{\partial^2 y}{\partial t^2}=-\omega^2 y_m \sin(kx-\omega t) \] \[k^{-2}\dfrac{\partial^2 y}{\partial x^2}= \omega^{-2}\dfrac{\partial^2 y}{\partial t^2}\] \[\dfrac{\partial^2 y}{\partial x^2}= \dfrac{k^2}{\omega^2} \dfrac{\partial^2 y}{\partial t^2}=\dfrac{1}{v^2}\dfrac{\partial^2 y}{\partial t^2}\] \[v=\dfrac{\omega}{k}\] 換句話說描述行進波的三角函數一樣滿足波方程式。更廣義的來說任何函數只要可以寫成下面的形式,都一定是波動方程式的解: \[y(x,t)=\Psi(x \pm vt).\] 下列的微分運作就再證明這樣的函數是波動方程式的解: \[u=x \pm vt\] \[\dfrac{\partial y}{\partial x}=\dfrac{d\Psi(u)}{du} \dfrac{\partial u}{\partial x}=\dfrac{d\Psi(u)}{du} \] \[\dfrac{\partial^2 y}{\partial x^2}=\dfrac{d^2 \Psi(u)}{du^2} \dfrac{\partial u}{\partial x}=\dfrac{d^2 \Psi(u)}{du^2} \] \[\dfrac{\partial y}{\partial t}=\dfrac{d\Psi(u)}{du} \dfrac{\partial u}{\partial t}=\dfrac{d\Psi(u)}{du} (\pm v)\] \[\dfrac{\partial^2 y}{\partial t^2}=\dfrac{d^2 \Psi(u)}{du^2} \dfrac{\partial u}{\partial t}(\pm v)=\dfrac{d^2 \Psi(u)}{du^2}(\pm v)^2=v^2 \dfrac{d^2 \Psi(u)}{du^2} \] \[\dfrac{1}{v^2} \dfrac{\partial^2 y}{\partial t^2}= \dfrac{d^2 \Psi(u)}{du^2}=\dfrac{\partial^2 y}{\partial x^2} \]波動方程式的波函數所描述的物理量就是在空間中傳播的物理性質,例如在一個水面上傳遞的是水面的高度\(y\)就代表水面的高度,在水面上傳的的水波就是這個高度變化在空間中傳遞出去。如果外所描述的是聲波,那麼\(y\)所描述的就是氣體分子的密度\(\rho\)在時空中的變化,密度的高低起伏在空間中傳播就是聲波。繩波函數就是在描述繩子離開平衡點高低起伏的變化在空間中傳遞,描述這樣傳遞的波動就是繩波函數所描述的內容。電磁波或者光波在傳遞的是電場和磁場的大小高低起伏變化,因此如果\(y\)描述電磁波,\(y\)可能是電場或磁場。所有這些波無論是否需要介質存在,他們所具備的數學性質和他們所必須滿足的方程式,在數學的結構上都是一樣的。
19世紀初的時候Thomas Young的雙狹縫實驗證實光是一種波動現象,所以光在空間中運動是一種光波的傳遞現象,但是當時並不知道這個波到底在傳遞什麼物理性質。一直到19世紀下半葉,英國物理學家馬克斯威爾(Maxwell)完備了整個電磁學的所有定律,並且從所有定律的數學結構中發現電磁場中存在波動現象,因此預言了自然界存在電磁波,而且傳遞的速度就是光速,進而得到光波應該就是廣義的電磁波當中的一個成員。後來這個電磁波在馬克斯威爾過世之後,由德國物理學家Hertz證實了無線電波的存在,也就證實了馬克斯威爾的電磁波理論是正確的。雖然我們已經接受光是一種波動現象,而且是一種電磁波,但是就在Hertz的實驗中,其實也隱約的發現光似乎有另外一種性質存在,那就是光電效應中所支持的光的粒子性。光被視為一種粒子是愛因斯坦在1905年提出來的光子說,愛因斯坦也因為光子的理論獲得諾貝爾獎。
二十世紀所發展的量子力學甚至於告訴我們,一般的物質在微觀世界中也會展現出波動的性質,我們稱呼為物質波。一個從電子槍射出來的電子,它在空間中運動的時候其實會以一種波動的形式在空間中傳遞。我們並不能十分掌握這個電子出現的位置和速度,取而代之的是我們只能描述這個電子會像波一樣,在什麼時間出現在什麼位置的可能機率,這樣的描述方式是完全違反我們日常生活經驗中對粒子的認知,這也是為什麼量子力學是那麼一個迷人的理論。並且這個微觀世界中的量子力學理論對我們人類的生活造成了非常大的改變,因此學習近代物理可以帶給一個人豐富收穫的愉快經驗。