GPS1-L10

Problem 1
The angular position of a point on the rim of a rotating wheel is given by \(\theta(t)=4.0t - 3.0t^2 + t^3\), where \(\theta\) is in radians and t is in seconds. What are the angular velocities at (a) t = 2.0 s and (b) t = 4.0 s? (c) What is the average angular acceleration for the time interval that begins at t = 2.0 s and ends at t = 4.0 s? What are the instantaneous angular accelerations at (d) the beginning and (e) the end of this time interval?
旋轉輪緣上的點的角位置由\(\theta(t)= 4.0t-3.0t^2 + t^3 \)給出，其中\(\theta \)的弧度和t 以秒為單位。 (a)t = 2.0 s和(b)t = 4.0 s時的角速度是多少？ (c)從t = 2.0 s到t = 4.0 s的時間間隔的平均角加速度是多少？ 在此時間間隔的開始(d)和(e)結束時的瞬時角加速度是多少？ (05小題)

(a)\(\omega(2)\)=______ rad./s

01: ANS:=4.0

(b)\(\omega(4)\)=______ rad./s

02: ANS:=28

(c)the average angular acceleration=_____ rad./s

03: ANS:=12

(d)\(\alpha(2)\)=_____ rad./s2

04: ANS:=6

(e)\(\alpha(4)\)=_____ rad./s2

05: ANS:=18

Solution:

Problem 2
A.The angular speed of an automobile engine is increased at a constant rate from 1200 rev/min to 3000 rev/min in 12 s. (a) What is its angular acceleration? (b) How many revolutions does the engine make during this 12 s interval?
汽車發動機的角速度在12 s內以恆定速率從1200轉/分鐘增加到3000轉/分鐘。 (a)它的角加速度是多少？ (b)在這12秒鐘的間隔內，發動機旋轉了多少圈？ (02小題)

(a)\(\alpha\)=____ rad./s2

06: ANS:=15.708

(b)number of revolutions=_____

07: ANS:=420

Solution:

Problem 2
B.What are the magnitudes of (a) the angular velocity, (b) the radial acceleration, and (c) the tangential acceleration of a spaceship taking a circular turn of radius 3220 km at a constant speed of 29000 km/h?
一以恆定速度29000 km/h旋轉半徑3220 km進行圓週運動的太空船，其（a）角速度，（b）徑向加速度和（c）切向加速度的大小是多少？ (03小題)

(a)\(\omega\)=____ rad./s

08: ANS:=2.5E-3

(b)radial acceleration, \(a_r\)=_____ m/s2

09: ANS:=20.2

(c)tangential acceleration, \(a_t\)=_____ m/s2

10: ANS:=0

Solution:

Problem 3
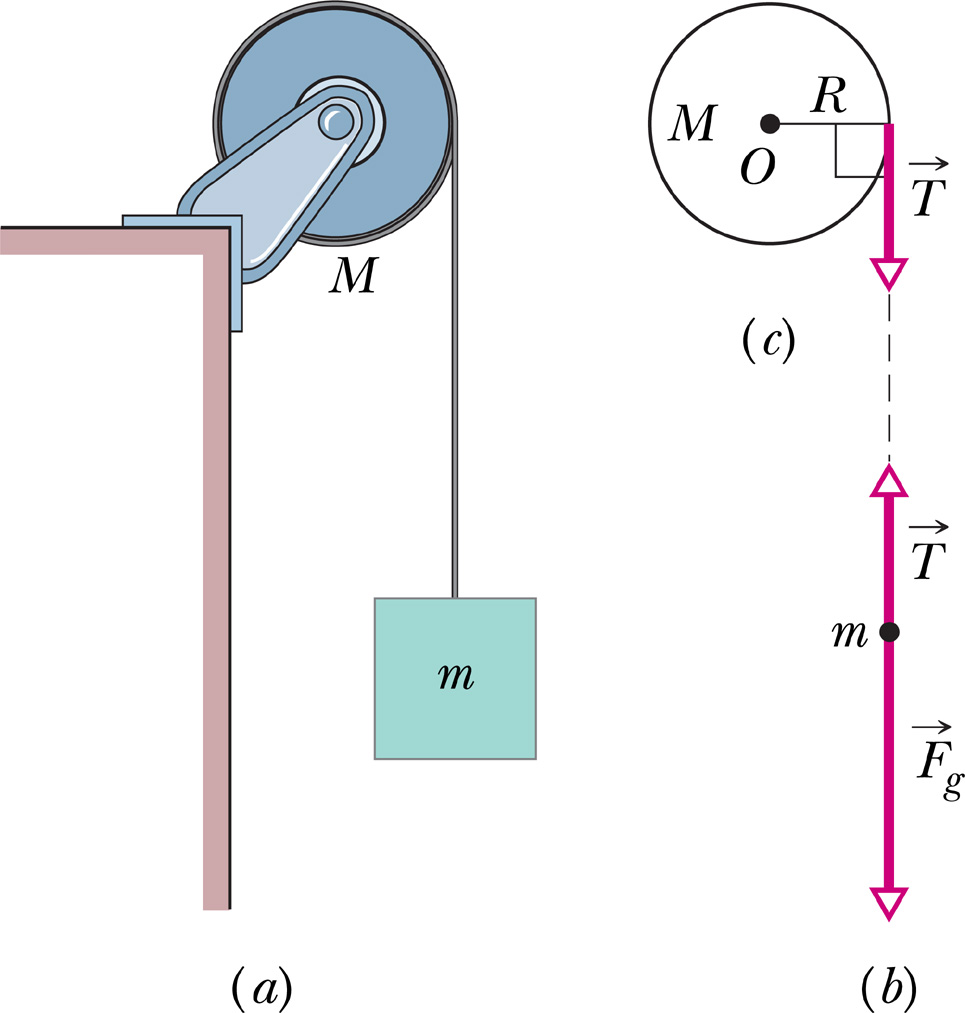The figure shows a uniform disk, with mass \(M=0.5\) kg and radius \(R=20\) cm, mounted on a fixed horizontal axle. A block with mass \(m=2.5\) kg hangs from a massless cord that is wrapped around the rim of the disk. Find (a)the acceleration of the falling block, (b)the angular acceleration of the disk, and (c)the tension in the cord. The cord does not slip, and there is no friction at the axle.
圖中顯示了質量為\(M = 0.5\)kg，半徑\(R = 20 \) cm的均勻盤，該盤安裝在固定的水平軸上。 質量為\(m = 2.5 \) kg的塊懸掛在纏繞在盤邊緣上的無質量繩索上。 計算(a)下降塊的加速度，(b)圓盤的角加速度和(c)繩索中的張力。 線不打滑，並且軸上沒有摩擦。 (03小題)

(a)the magnitude of the acceleration of the block, \(|a|\)=_______\(m/s^2\)

11: ANS:=8.909

(b)the magnitude of the angular acceleration of the disk, \(|\alpha|\)=_________\(rad/s^2\)

12: ANS:=44.55

(c)the tension in the cord=______ N

13: ANS:=2.227

Solution:

(a)block:\(mg-T=ma\)

disk:\(\tau=r F_t=RT\)

\(\tau_{net}=I\alpha\)

\(I=\frac{1}{2}MR^2\)


\(RT=\frac{1}{2}MR^2 \alpha\)

\(a_t=R\alpha \to\to \alpha=\dfrac{a}{R}\)

\(T=\frac{1}{2}Ma\)

\(ma=mg-T=mg - \frac{1}{2}Ma\)

\(a=g\frac{2m}{M+2m}=(9.8m/s^2)\dfrac{2(2.5kg)}{0.5kg+2(2.5kg)}=8.909m/s^2\)

(b)
\(\alpha=\dfrac{a}{R}=\dfrac{8.909m/s^2}{0.2m}=44.545 rad/s^2\)

(c)
\(T=\frac{1}{2}Ma=\frac{1}{2}(0.5kg)(8.909m/s^2)=2.227 N\)
Problem 4
When a slice of buttered toast is accidentally pushed over the edge of a counter, it rotates as it falls. If the distance to the floor is \(76\) cm and for rotation less than \(1\) rev, what are the (a) smallest and (b) largest angular speeds that cause the toast to hit and then topple to be butter-side down?
當一片奶油吐司意外地推到櫃檯的邊緣時，它會隨著下落而旋轉。 如果與地面的距離為\(76 \) cm，並且旋轉小於1轉，導致吐司撞擊地面然後翻倒的奶油面朝下的最小(a)和(b)最大角速度是多少？ (02小題)

(a) smallest angular speed=______rad/s

14: ANS:=4

(b) largest angular speed=______rad/s

15: ANS:=12

Solution:

\(h=\frac{1}{2}gt^2\)

\(\Delta t=\sqrt{\dfrac{2h}{g}}=\sqrt{\dfrac{2(0.76m)}{9.8}}=0.394s\)

(a) 土司旋轉然後掉到地面時的最小角度為

\(\Delta \theta_{min}=0.25rev=\dfrac{\pi}{2}rad\)


（掉到地面土司旋轉不超過一圈，且A端掉下，旋轉後B端撞到地面）

\(\omega_{min}=\dfrac{\Delta \theta_{min}}{\Delta t}=\dfrac{\dfrac{\pi}{2}rad}{0.394s}=4rad/s\)

(b)\(\Delta \theta_{max}=0.75rev=\dfrac{3\pi}{2}rad\)

（掉到地面土司旋轉不超過一圈，且A端掉下，旋轉後D端撞到地面）

\(\omega_{max}=\dfrac{\Delta \theta_{max}}{\Delta t}=\dfrac{\dfrac{3\pi}{2}rad}{0.394s}=12rad/s\)
Problem 5
A diver makes 2.5 revolutions on the way from a \(10\) m high platform to the water. Assuming zero initial vertical velocity, find the average angular velocity during the dive.
跳水者在從10 m高的平台到水的過程中旋轉了2.5轉。假設初始垂直速度為零，求出在跳水期間平均角速率。 (01小題)

the average angular velocity=______rad/s

16: ANS:=11

Solution:

\(\Delta y=v_{0y}t-\frac{1}{2}gt^2\)

\(t=\sqrt{\dfrac{2\Delta y}{g}}=\sqrt{\dfrac{2(10m)}{9.8m/s^2}}=1.4s\)

\(\omega_{avg}=\dfrac{(2.5rev)(2\pi rad/rev)}{1.4s}=11rad/s\)
Problem 6
(a)計算以602轉/分鐘旋轉時具有24400 J動能的車輪的轉動慣量。假設車輪是一個質量均勻分佈的圓盤，車輪的半徑為80公分，(b)計算這個車輪的質量。 (02小題)

(a)I=______\(kg.m^2\)

17: ANS:=12.3

(b)計算這個車輪的質量，\(M\)=_____ kg

18: ANS:=38.37

Solution:

(a)\(K=\frac{1}{2}I \omega^2\)

\(I=\dfrac{2K}{\omega^2}=\dfrac{2(24,400)}{\left(\dfrac{(602)(2\pi)}{60}\right)^2}=12.29\) kg.m2
(b)\(I=1/2 M R^2; \,\,\, M=\dfrac{2I}{R^2}=38.37\)
nprob= 7 7

Problem 7
In the figure, two particles, each with mass m, are fastened to each other, and to a rotation axis at O, by two thin rods, each with length d and mass M_r. The combination rotates around the rotation axis with angular speed \(\omega\)=omega. Measured about O, what are the combination's (a) rotational inertia and (b) kinetic energy? 在圖中，每個質量為\(m\)的兩個粒子通過兩個長為\(d\)且質量為\(M_r\)=M_r的細棒相互固定，並固定在O的旋轉軸上。 組合繞旋轉軸以角速度\(\omega \)= omega旋轉。 求此組合的(a)轉動慣量和(b)動能是多少？ (02小題)

(a) rotational inertia=____ [m, M_r,d]

19: ANS:=8/3*M_r*d**2+5*m*d**2

(b) kinetic energy=_____ [m, M_r,d, omega]

20: ANS:=(4/3*M_r+5/2*m)*d**2*omega**2

Solution:


nprob= 7 7

Problem 7
Calculate the rotational inertia of a disk of mass M and radius R, about an axis perpendicular to the disk and passing through its center.
計算質量為M且半徑為R的圓盤繞垂直於圓盤並穿過圓盤中心的軸的旋轉慣量。 (01小題)

I=_____ [M,R]

21: ANS:=1/2*m*R**2

Solution:

\(I=\frac{1}{2}MR^2=\frac{1}{2}(2kg)(0.3m)^2=0.09 kg\cdot m^2\)
nprob= 8 8

Problem 8
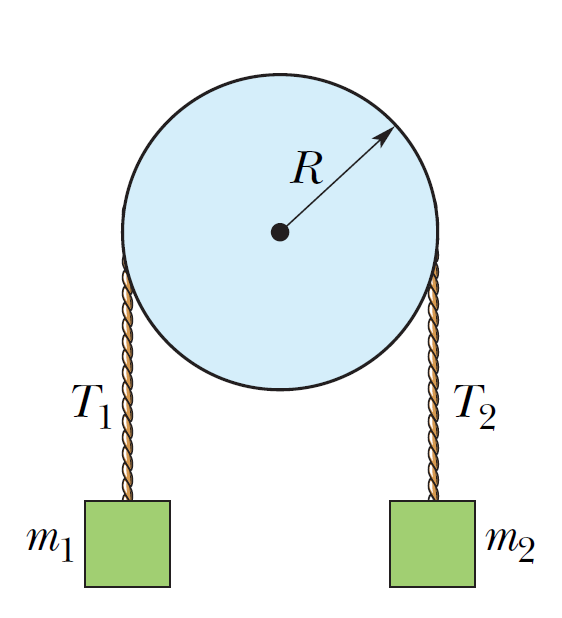In the figure, block 1 has mass m_1, block 2 has mass m_2, and the pulley, which is mounted on a horizontal axle with negligible friction, has radius R. When released from rest, block 2 falls a distance y in time t without the cord slipping on the pulley. (a) What is the magnitude of the acceleration of the blocks? What are (b) tension T_2 and (c) tension T_1? (d) What is the magnitude of the pulley's angular acceleration? (e) What is its rotational inertia?
在圖中，塊1的質量為m_1，塊2的質量為m_2，安裝在水平軸上且摩擦力可忽略的皮帶輪的半徑為R。從靜止狀態釋放時，塊2在時間t處下降了距離y ，線在滑輪上不打滑。 (a)塊的加速度是多少？ (b)張力T_2和(c)張力T_1是什麼？ (d)滑輪的角加速度的大小是多少？ (e)它的轉動慣量是多少？ (05小題)

(a)the acceleration \(a\)=_____ [y,t]

22: ANS:=2*y/t**2

(b)\(T_2\)=_____ [m_2,y,t,g]

23: ANS:=m_2*(g-2*y/t**2)

(c)\(T_1\)=_____ [m_1,y,t,g]

24: ANS:=m_1*(g+2*y/t**2)

(d)angular acceleration \(\alpha\)=______ [y,t,R]

25: ANS:=(2*y)/(R*t**2)

(e)moment of inertia of the pulley, I=_____ [T_1,T_2,R,alpha] alpha=\(\alpha\)=angular acceleration

26: ANS:=(T_2-T_1)*R/alpha

Problem 9
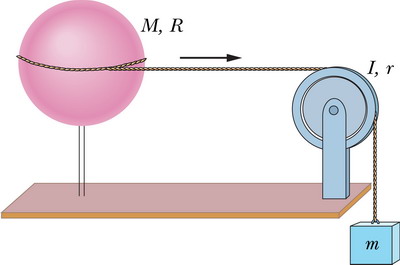A uniform spherical shell of mass \(M=4.5\) kg and radius \(R=8.5\) cm can rotate about a vertical axis on frictionless bearings (see figure). A massless cord passes around the equator of the shell, over a pulley of rotational inertia \(I=3.0 \times 10^{-3} \text{kg.m}^2\) and radius \(r=5.0\) cm, and is attached to a small object of mass \(m=0.60\) kg. There is no friction on the pulley's axle; the cord does not slip on the pulley. What is the speed of the object when it has fallen 82 cm after being released from rest? Use energy considerations.
質量為\(M = 4.5 \) kg，半徑為\(R = 8.5 \)cm的均勻球面殼可以在無摩擦軸承上繞垂直軸旋轉（見圖）。 一根無質量的繩索繞過殼體的赤道，繞過轉動慣量\(I = 3.0 \times 10^{-3} \rm {kg.m}^2 \)和半徑\(r = 5.0 \) cm，並附著在質量為\(m = 0.60 \) kg的小物體上。 皮帶輪的軸上沒有摩擦。 繩索沒有在滑輪上滑動。 物體從靜止釋放後掉落82 cm時的速度是多少？ 使用能量觀點來考慮此問題。 (01小題)

\(v\)=____ m/s

27: ANS:=1.42

Solution:

球殼轉動慣量為\(I_{shell}=\frac{2}{3}MR^2\)

\(K=\frac{1}{2}(\frac{2}{3}MR^2)\omega_{sphere}^2+\frac{1}{2}I\omega_{pulley}^2+\frac{1}{2}mv^2=mgh\)

\(\omega_{pully}=\dfrac{v}{r}\)

\(\omega_{sphere}=\dfrac{v}{R}\)

\(v=\sqrt{\dfrac{mgh}{\frac{1}{2}m+\frac{1}{2}\frac{I}{r^2}+\frac{M}{3}}}\)

\(=\sqrt{\dfrac{2gh}{1+\frac{I}{mr^2}+\frac{2M}{3m}}}\)

\(=\sqrt{\dfrac{2(9.8)(0.82)}{1+\dfrac{3\times 10^{-3}}{(0.6)(0.05)^2}+\dfrac{2(4.5)}{3(0.6)}}}\)

\(=1.42\) m/s
Problem 10
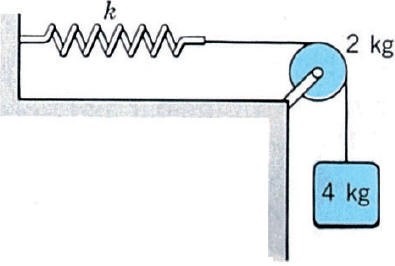The figure shows a block of mass 4 kg suspended by a rope that passes over a pulley of mass 2 kg and radius 5 cm. The rope is connect to a spring whose stiffness constant is 80 N/m. (a) If the block is released from rest, what is the maximum extension of the spring? (b) what is the speed of the block after it has fallen 20 cm? Treat the pulley as a disk.
圖中顯示了一塊質量為4kg的質量塊，該質量塊由一條繩索懸掛，該繩索穿過質量為2 kg，半徑為5 cm的滑輪。 繩索連接彈性係數為80 N/m的彈簧。 (a)如果將塊從靜止狀態釋放，則彈簧的最大伸長量是多少？ (b)砌塊下降20 cm後的速度是多少？ 將皮帶輪當作圓盤。 (02小題)

(a)\(x\)=______m

28: ANS:=0.98

(b)\(v\)=______m/s

29: ANS:=1.58

Solution:

\(\Delta E=\frac{1}{2}mv^2+\frac{1}{2}I(\frac{v}{R})^2+\frac{1}{2}kx^2-mgx=0\)

(a)
\(v=0\)

\(\Delta E=\frac{1}{2}kx^2-mgx=0\)

\(x=\dfrac{2mg}{k}=\dfrac{2(4kg)(9.8m/s^2)}{80N/m}=0.98m\)

\(I=\frac{1}{2}mR^2=\frac{1}{2}(2kg)(0.05m)^2\)\(\to \to \dfrac{I}{R^2}=\frac{1}{2}m=\frac{1}{2}(2kg)=1kg\)

(b)
\(\Delta E=\frac{1}{2}(4kg)v^2+\frac{1}{2}(\dfrac{I}{R^2})v^2+\frac{1}{2}(80N/m)(0.2m)^2-(4kg)(9.8m/s^2)(0.2m)=0\)

\(v=1.58 m/s\)