User: the primitive translation vectors of hcp lattice
ChatGPT: In the hexagonal close-packed (hcp) lattice, the primitive translation vectors define the repeating unit of the crystal structure in three-dimensional space. The hcp structure has two atoms per unit cell and a hexagonal symmetry. The primitive translation vectors for the hcp lattice can be written as:
User: the volume of the primitive cell
ChatGPT: The volume of the primitive unit cell for a hexagonal close-packed (hcp) lattice can be calculated using the primitive translation vectors \(\mathbf{a}_1\), \(\mathbf{a}_2\), and \(\mathbf{a}_3\). The volume \(V_{\text{primitive}}\) of the primitive cell is given by the scalar triple product of the primitive translation vectors: \[ V_{\text{primitive}} = | \mathbf{a}_1 \cdot (\mathbf{a}_2 \times \mathbf{a}_3) | \] The primitive translation vectors for the hcp lattice are: \[ \mathbf{a}_1 = a \hat{i} \] \[ \mathbf{a}_2 = a \left( \frac{1}{2} \hat{i} + \frac{\sqrt{3}}{2} \hat{j} \right) \] \[ \mathbf{a}_3 = c \hat{k} \] Now, we need to compute the cross product \(\mathbf{a}_2 \times \mathbf{a}_3\) and then the dot product \(\mathbf{a}_1 \cdot (\mathbf{a}_2 \times \mathbf{a}_3)\). 1. **Cross product** \(\mathbf{a}_2 \times \mathbf{a}_3\): \[ \mathbf{a}_2 \times \mathbf{a}_3 = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a \left( \frac{1}{2} \hat{i} + \frac{\sqrt{3}}{2} \hat{j} \right) & 0 & c \hat{k} \end{vmatrix} \] Performing the determinant: \[ \mathbf{a}_2 \times \mathbf{a}_3 = a c \left( \frac{\sqrt{3}}{2} \hat{i} - \frac{1}{2} \hat{j} \right) \] 2. **Dot product** \(\mathbf{a}_1 \cdot (\mathbf{a}_2 \times \mathbf{a}_3)\): \[ \mathbf{a}_1 \cdot (\mathbf{a}_2 \times \mathbf{a}_3) = a \hat{i} \cdot \left( a c \left( \frac{\sqrt{3}}{2} \hat{i} - \frac{1}{2} \hat{j} \right) \right) \] This simplifies to: \[ \mathbf{a}_1 \cdot (\mathbf{a}_2 \times \mathbf{a}_3) = a^2 c \frac{\sqrt{3}}{2} \] Thus, the volume of the primitive unit cell is: \[ V_{\text{primitive}} = \left| a^2 c \frac{\sqrt{3}}{2} \right| \] Finally, the volume of the primitive cell is: \[ V_{\text{primitive}} = \frac{\sqrt{3}}{2} a^2 c \]
User: packing fraction of hcp
ChatGPT: The packing fraction (also called the packing efficiency) of a crystal structure is the fraction of the volume of the unit cell that is occupied by the atoms. For the hexagonal close-packed (hcp) structure, the packing fraction can be determined by calculating the ratio of the total volume occupied by atoms to the volume of the unit cell. 1. **Atoms per unit cell**: In an hcp lattice, there are 2 atoms per unit cell. This comes from the fact that: - One atom is located entirely within the unit cell. - The second atom is located at \(\left( \frac{1}{3}, \frac{2}{3}, \frac{1}{2} \right)\), which is equivalent to an atom at the top of the unit cell, contributing half of its volume to the unit cell. 2. **Volume of the unit cell**: As we previously calculated, the volume of the primitive unit cell for the hcp lattice is: \[ V_{\text{primitive}} = \frac{\sqrt{3}}{2} a^2 c \] 3. **Volume of each atom**: The volume of an individual atom is given by the formula for the volume of a sphere: \[ V_{\text{atom}} = \frac{4}{3} \pi r^3 \] The relationship between the atomic radius \(r\) and the lattice constant \(a\) for the hcp structure is: \[ r = \frac{a}{2} \] Thus, the volume of each atom becomes: \[ V_{\text{atom}} = \frac{4}{3} \pi \left( \frac{a}{2} \right)^3 = \frac{\pi a^3}{6} \] 4. **Total volume occupied by atoms**: Since there are 2 atoms per unit cell, the total volume occupied by atoms is: \[ V_{\text{atoms}} = 2 \times \frac{\pi a^3}{6} = \frac{\pi a^3}{3} \] 5. **Packing fraction**: The packing fraction \(\text{PF}\) is the ratio of the volume occupied by the atoms to the total volume of the unit cell: \[ \text{PF} = \frac{V_{\text{atoms}}}{V_{\text{primitive}}} \] Substituting the expressions for \(V_{\text{atoms}}\) and \(V_{\text{primitive}}\): \[ \text{PF} = \frac{\frac{\pi a^3}{3}}{\frac{\sqrt{3}}{2} a^2 c} \] Simplifying: \[ \text{PF} = \frac{2 \pi a^3}{3 \sqrt{3} a^2 c} \] \[ \text{PF} = \frac{2 \pi a}{3 \sqrt{3} c} \] 6. **Relationship between \(a\) and \(c\)**: For an ideal hcp structure, the ratio of \(c\) to \(a\) is: \[ \frac{c}{a} = \sqrt{\frac{8}{3}} \approx 1.633 \] Substituting this value into the expression for packing fraction: \[ \text{PF} = \frac{2 \pi a}{3 \sqrt{3} \times \sqrt{\frac{8}{3}} a} \] Simplifying: \[ \text{PF} = \frac{\pi}{\sqrt{8}} \approx 0.74048 \] Therefore, the packing fraction of the hcp lattice is approximately **0.740** or **74.0%**.
User: packing fraction of FCC
ChatGPT: The packing fraction (or packing efficiency) of the face-centered cubic (FCC) lattice can be determined by calculating the ratio of the volume occupied by the atoms to the total volume of the unit cell. 1. **Atoms per unit cell**: In an FCC lattice, there are 4 atoms per unit cell. This is because: - There is **1 atom at each corner** of the cube, and each corner atom is shared by 8 neighboring unit cells, so each contributes \(\frac{1}{8}\) of an atom to the unit cell. Since there are 8 corners, the total contribution from the corner atoms is \(8 \times \frac{1}{8} = 1\) atom. - There is **1 atom at the center of each face** of the cube, and each face-centered atom is shared by 2 unit cells, so each contributes \(\frac{1}{2}\) of an atom. Since there are 6 faces, the total contribution from the face-centered atoms is \(6 \times \frac{1}{2} = 3\) atoms. Therefore, the total number of atoms per FCC unit cell is \(1 + 3 = 4\) atoms. 2. **Volume of the unit cell**: The volume of the unit cell for the FCC lattice is given by the cube of the edge length \(a\), so the total volume of the unit cell is: \[ V_{\text{unit cell}} = a^3 \] 3. **Volume of each atom**: The volume of an individual atom is given by the formula for the volume of a sphere: \[ V_{\text{atom}} = \frac{4}{3} \pi r^3 \] The relationship between the atomic radius \(r\) and the lattice constant \(a\) for the FCC structure is: \[ a = 2\sqrt{2}r \] Thus, the volume of each atom becomes: \[ V_{\text{atom}} = \frac{4}{3} \pi \left( \frac{a}{2\sqrt{2}} \right)^3 = \frac{\pi a^3}{6\sqrt{2}} \] 4. **Total volume occupied by atoms**: Since there are 4 atoms per unit cell, the total volume occupied by atoms is: \[ V_{\text{atoms}} = 4 \times \frac{\pi a^3}{6\sqrt{2}} = \frac{2\pi a^3}{3\sqrt{2}} \] 5. **Packing fraction**: The packing fraction \(\text{PF}\) is the ratio of the volume occupied by the atoms to the total volume of the unit cell: \[ \text{PF} = \frac{V_{\text{atoms}}}{V_{\text{unit cell}}} \] Substituting the expressions for \(V_{\text{atoms}}\) and \(V_{\text{unit cell}}\): \[ \text{PF} = \frac{\frac{2\pi a^3}{3\sqrt{2}}}{a^3} \] Simplifying: \[ \text{PF} = \frac{2\pi}{3\sqrt{2}} \approx 0.74048 \] Therefore, the packing fraction of the FCC lattice is approximately **0.740** or **74.0%**.
Given that Sodium transforms from bcc to hcp structure at about T =\(23^{\circ}\)K, and assuming the density remains fixed, and the c/a ratio is ideal, we need to calculate the hcp lattice spacing \(a\). We are given that the cubic lattice spacing \(a' = 4.23 \, \text{Å}\) in the bcc phase.
The lattice spacing \(a\) for the hcp structure is approximately 3.77 Å.
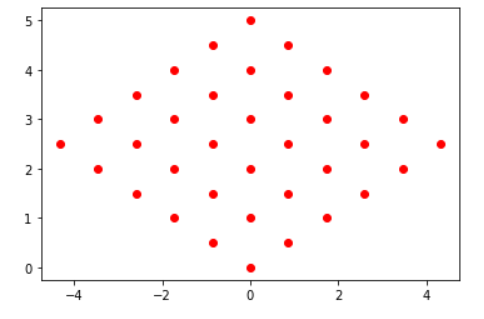
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
a1=np.array([np.sqrt(3)/2,1/2])
a2=np.array([-np.sqrt(3)/2,1/2])
for i in range(6):
for j in range(6):
c=i*a1+j*a2
#print(i,j,c)
plt.plot(c[0],c[1],'ro')
ºû®æ¯Ç-Áɯ÷ìM(WIKI)