愛因斯坦－德哈斯效應（德文：Einstein-de-Haas-Effekt），又稱作理查森效應（英文：Richardson effect，名從物理學家歐文·理查森）
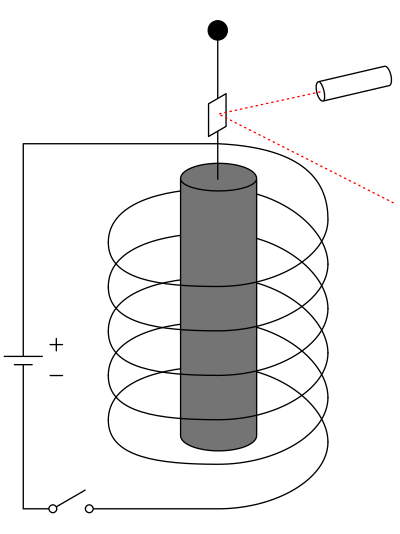是由阿爾伯特·愛因斯坦和萬德爾·德哈斯在1910年代中期觀測並描述的物理現象；此效應揭示了基本粒子的磁場、角動量和自旋之間的關係。此現象所描述的是，一個依靠細線懸掛在導體線圈中的鐵磁體（圓柱體並原先保持靜止狀態），在線圈上加有一個電流脈衝後會產生鐵磁體的力學轉動。對應著這個力學轉動，鐵磁體將具有一個特定的角動量，因此根據角動量守恆定律需要在鐵磁體內部產生一個等大反向的角動量來補償。考慮到由線圈中的電流所產生的外加磁場會引發鐵磁體中電子自旋的磁化（或通過選取特定的電流方向，使已經磁化的鐵磁體中的電子自旋反向），愛因斯坦-德哈斯效應反映了量子力學中的自旋角動量和古典力學中的轉動角動量具有相同的自然本質。值得注意的是，量子化的電子自旋是不能在古典力學的框架下描述的。
朗德g因子(Wiki)
Lande g-Factor Explanation
The Lande g-factor (\(g_s\)) is an important quantity in quantum mechanics that describes the magnetic moment of an electron due to its spin. The value of \(g_s\) is approximately 2 for a free electron.
1. Magnetic Moment from Spin
The magnetic moment (\(\mu\)) of a particle with spin is related to its spin angular momentum (\(S\)) by the equation:
\[ \mu = g \frac{e}{2m} S \]
Where:
- \(g\) is the g-factor.
- \(e\) is the elementary charge.
- \(m\) is the mass of the particle.
2. Intrinsic Spin of the Electron
The electron is a fundamental particle with a spin of \(\frac{1}{2}\). This intrinsic property contributes to the overall magnetic moment of the electron.
3. Relativistic Effects
The Dirac equation, which describes relativistic electrons, predicts that the g-factor for a free electron is exactly 2. This result stems from the combination of the electron's spin and its relativistic properties.
4. Corrections and Anomalies
While the theoretical value of \(g_s\) is 2, precise measurements show that the actual g-factor of the electron is slightly greater than 2 due to quantum electrodynamic (QED) effects. This is expressed as:
\[ g_s = 2 + \Delta g \]
Where \(\Delta g\) accounts for these higher-order corrections.
Conclusion
The Lande factor \(g_s = 2\) arises from the intrinsic properties of the electron and its relativistic behavior. The slight deviation observed in experiments is a result of QED effects, leading to the concept of the anomalous magnetic moment.