-
time-independent Schrodinger Equation in 1D
-
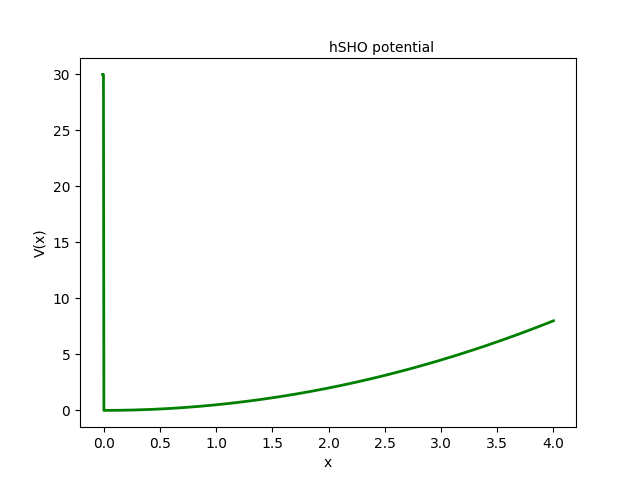
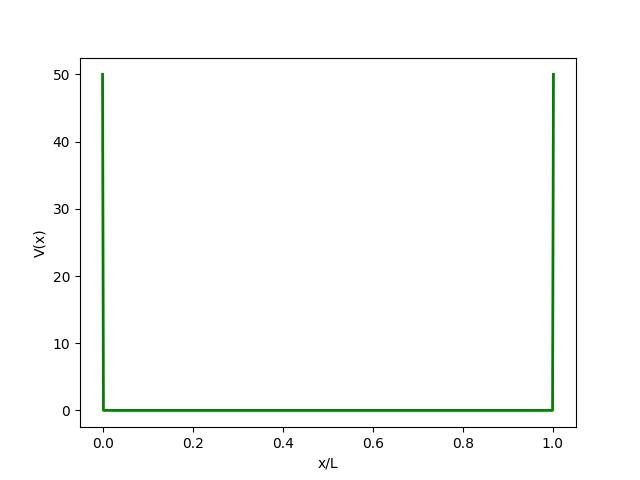
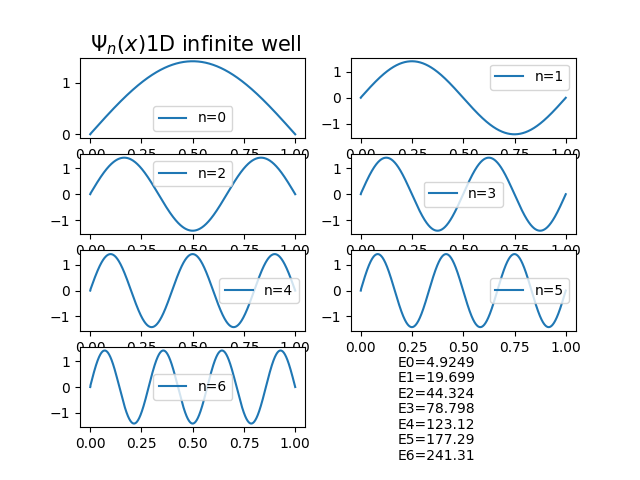
無窮位能井
-
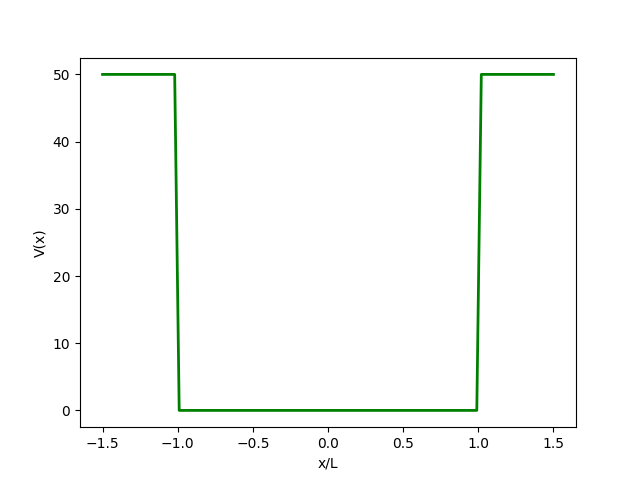
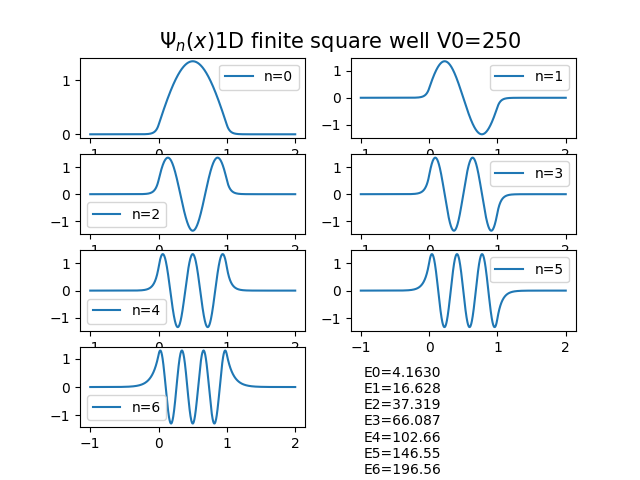
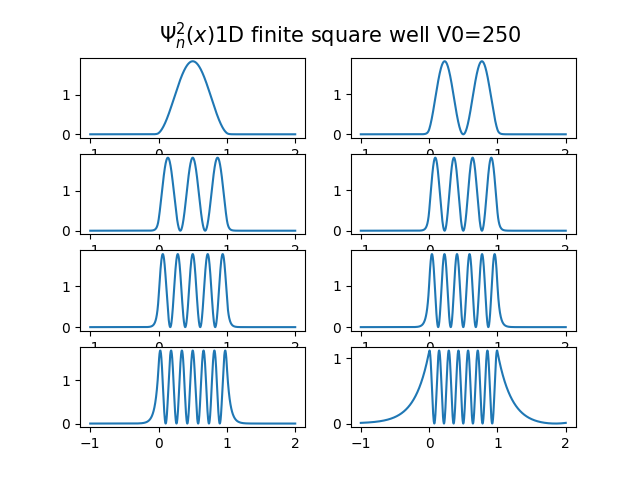
有限位能井
-
簡諧振子
-
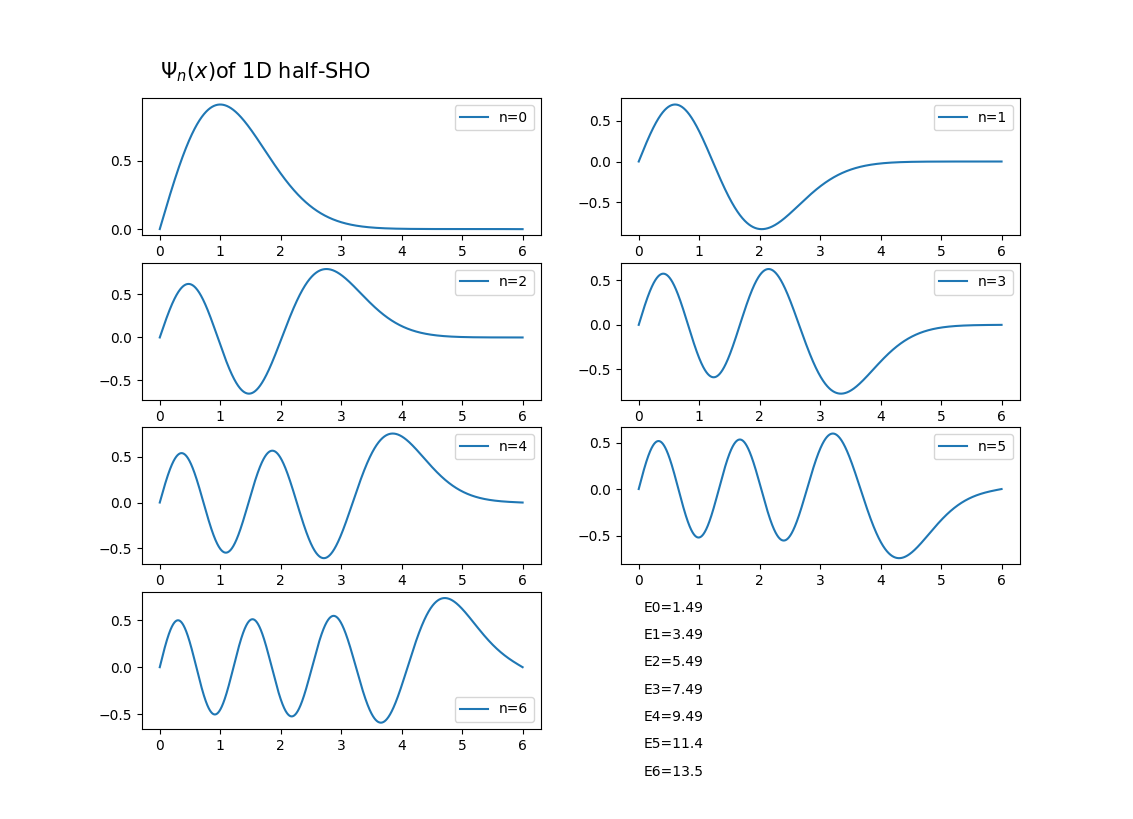
半簡諧振子
- 找到更高的本徵能量以及本徵波函數所對應的圖形
一維量子力學問題的數值解
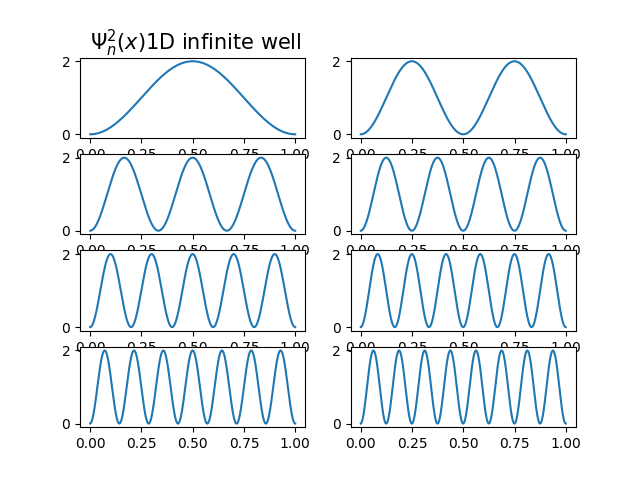
最簡單的例子--無窮位能井 \[位能函數:V(x) = \left\{ \begin{array}{lr} 0 & , 0 \le x \le L\\ \infty & , \textrm{otherwise} \end{array} \right. \] 這是一個可以精確解的問題,其本徵態和本徵能量分別為 \[ \Psi(x)=\sqrt{\frac{1}{L} }\sin\left(\frac{n\pi}{L}x\right) \] \[ E_n=\frac{h^2}{8mL^2}n^2=\frac{4\pi^2}{8}\frac{\hbar^2}{mL^2}n^2 \] 若取\(\hbar=1, m=1, L=1\)則 (\(4\pi^2/8 \simeq 4.9348\)) \[ E_n= 4.9348 n^2 \]
針對這樣一個二階微分方程式,最簡單的數值處理方法就是利用中間值法(Verlet method): \[ \Psi(x+h)=2\Psi(x)-\Psi(x-h)+h^2 D(x) \]
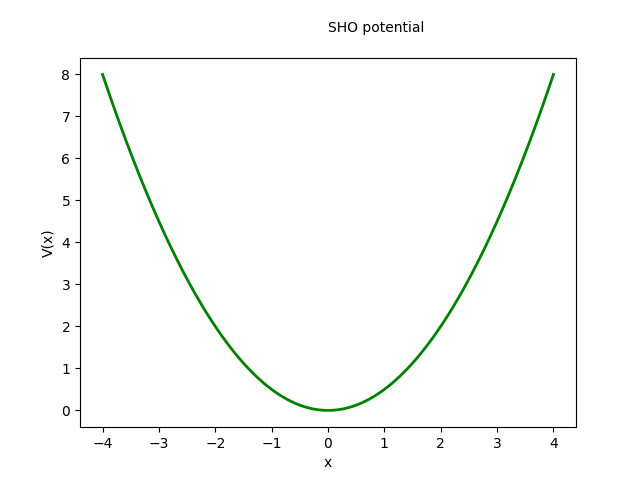
簡諧振子的位能函數: \[ V(x)=1/2 k x^2=1/2 m\omega^2 x^2 \] 本徵能量: \[ E_n=\hbar \omega \left( n+ {1 \over 2} \right)=(2n+1) {\hbar \over 2} \omega \] 本徵波函數: \[ \psi_{n}(x)=\frac{1}{\sqrt{2^{n} n!}} \cdot \left(\frac{m\omega}{\pi \hbar}\right)^{1/4} \cdot e^{-\frac {m\omega x^{2}}{2\hbar}} \cdot H_{n}\left( \sqrt{\frac{m\omega}{\hbar}}x\right) \] \[ \qquad n=0,1,2,\ldots .\] The functions \(H_n\) are the physicists' Hermite polynomials, \[ H_{n}(z)=(-1)^{n}~e^{z^{2}}\frac {d^{n}}{dz^{n}} \left(e^{-z^2} \right). \] The first eleven physicists' Hermite polynomials are:
\begin{aligned}H_{0}(x)&=1,\\H_{1}(x)&=2x,\\H_{2}(x)&=4x^{2}-2,\\H_{3}(x)&=8x^{3}-12x,\\H_{4}(x)&=16x^{4}-48x^{2}+12,\\H_{5}(x)&=32x^{5}-160x^{3}+120x,\\H_{6}(x)&=64x^{6}-480x^{4}+720x^{2}-120,\\H_{7}(x)&=128x^{7}-1344x^{5}+3360x^{3}-1680x,\\H_{8}(x)&=256x^{8}-3584x^{6}+13440x^{4}-13440x^{2}+1680,\\H_{9}(x)&=512x^{9}-9216x^{7}+48384x^{5}-80640x^{3}+30240x,\\H_{10}(x)&=1024x^{10}-23040x^{8}+161280x^{6}-403200x^{4}+302400x^{2}-30240.\end{aligned}
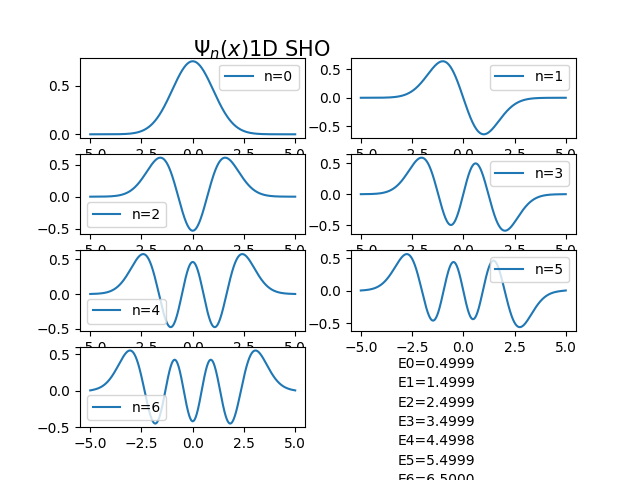
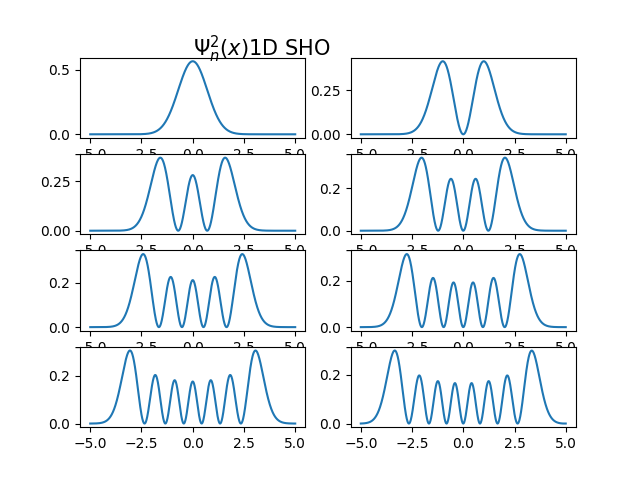
練習