-
用精確解作動畫
-
加入彈簧
-
以差分近似來模擬簡諧運動
差分近似 -
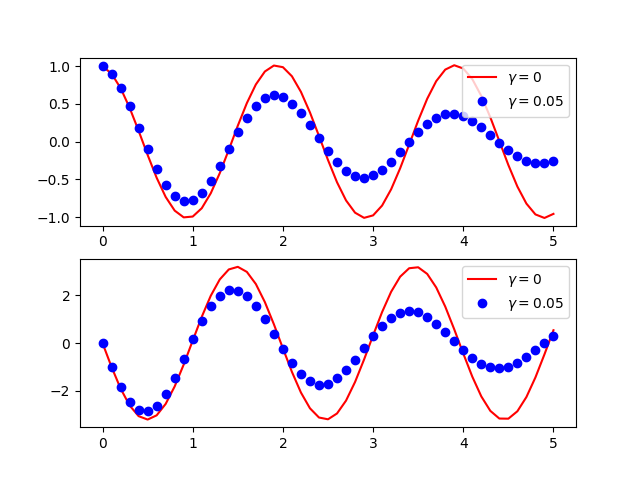
比較有阻力作用下之簡諧運動
\[a=-\frac{kx}{m}-\gamma v\]
-
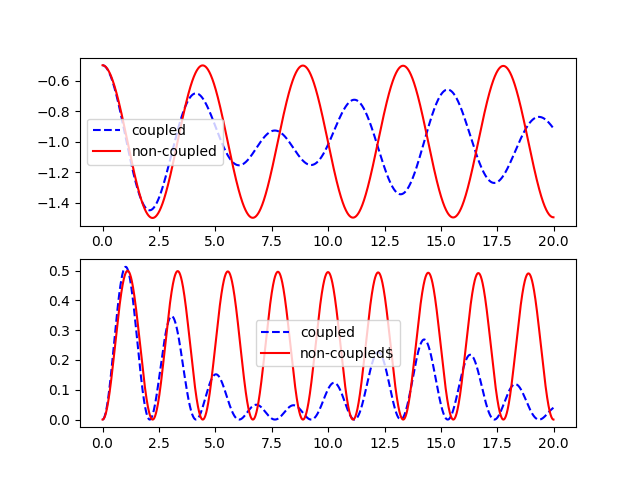
偶合震盪的模擬-台北101阻尼器
以差分近似模擬簡諧運動
簡諧運動的運動方程式與精確解
簡諧運動的運動方程式# coding=Big5 from visual import * x0=1.; k=10.; m=1.; w=sqrt(k/m); T=2.*pi/w A=x0 scene=display(width=800,height=800,center=(0,0,0),background=(0.5,0.5,0)) ball1=sphere(pos=(x0,0,0),radius =0.1,color=(0,0,0)) X=arrow(pos=(-2,0,0), axis=(4,0,0), shaftwidth=0.03) L=20 for i in range(-L,L+1): x=0.1*i if(i%10==0): k=2 label(pos=(x,-0.2,0),text='%2d' % int(x),height=20,color=(0,0,0),box=False) else: k=1 arrow(pos=(x,0,0),axis=(0,0.2*k,0),shaftwidth=0.02) t,dt=0.,0.01 while (t<10.): t+=dt rate(int(1./dt)/2) #精確解------------------ ball1.pos.x=A*cos(w*t)
# coding=Big5
from visual import *
x0=1.; k=10.; m=1.; w=sqrt(k/m); T=2.*pi/w
A=x0
scene=display(width=800,height=800,center=(0,0,0),background=(0.5,0.5,0))
ball1=sphere(pos=(x0,0,0),radius =0.1,color=(0,0,0))
spring=helix(pos=(-2,0,0),axis=(3,0,0),radius=0.1,width=0.01,color=(1,0,0))
X=arrow(pos=(-2,0,0), axis=(4,0,0), shaftwidth=0.03)
L=20
for i in range(-L,L+1):
x=0.1*i
if(i%10==0):
k=2
label(pos=(x,-0.2,0),text='%2d' % int(x),height=20,color=(0,0,0),box=False)
else: k=1
arrow(pos=(x,0,0),axis=(0,0.2*k,0),shaftwidth=0.02)
t,dt=0.,0.01
while (t<10.):
t+=dt
rate(int(1./dt)/2)
#精確解------------------
ball1.pos.x=A*cos(w*t)
spring.axis=(ball1.pos.x+2,0,0)
# coding=Big5
from visual import *
def ruler():
X=arrow(pos=(-2,0,0), axis=(4,0,0), shaftwidth=0.03)
L=20
for i in range(-L,L+1):
x=0.1*i
if(i%10==0):
k=2
label(pos=(x,-0.2,0),text='%2d' % int(x),height=20,color=(0,0,0),box=False)
else: k=1
arrow(pos=(x,0,0),axis=(0,0.2*k,0),shaftwidth=0.02)
x0=1.; k=10.; m=1.; w=sqrt(k/m); T=2.*pi/w; A=x0
x,v=x0,0.
scene=display(width=800,height=800,center=(0,0,0),background=(0.5,0.5,0))
ball1=sphere(pos=(x0,0,0),radius =0.05,color=(0,0,0))
ball2=sphere(pos=(x0,0,0),radius =0.1,color=color.blue,opacity=0.2)
ruler()
t,dt=0.,0.1
while (t<10.):
t+=dt
rate(int(1./dt)/2)
#精確解------------------
ball1.pos.x=A*cos(w*t)
#差分近似----------------
v+=-k/m*x*dt
x+=v*dt
ball2.pos.x=x
import matplotlib
import matplotlib.pyplot as plt
matplotlib.use("Agg")
import numpy as np
x0=1.; k=10.; m=1.
w=np.sqrt(k/m); T=2.*np.pi/w; A=x0
x,xe,v=x0,x0,0.
t=0.; dt=0.1; Lt=[]; Lxe=[]; Lx=[]; Lv=[]
while (t < 5.):
Lt.append(t);Lxe.append(xe)
Lx.append(x); Lv.append(v)
t+=dt
#精確解------------------
xe=A*np.cos(w*t)
#差分近似----------------
v+=-k/m*x*dt
x+=v*dt
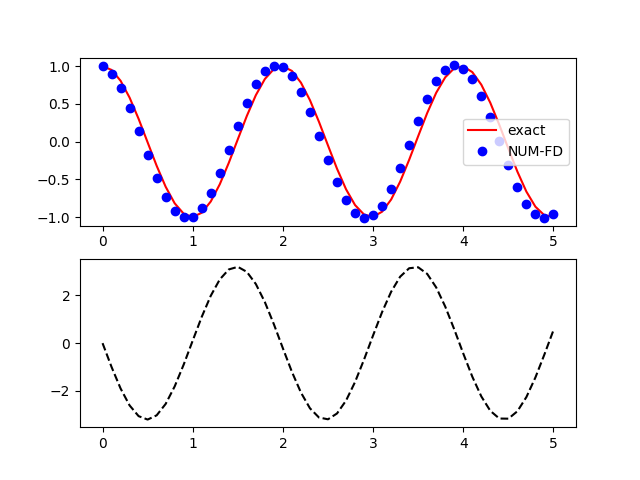
plt.subplot(211)
plt.plot(Lt,Lxe,'r-', label="exact")
plt.plot(Lt,Lx,'bo', label="NUM-FD")
plt.legend()
plt.subplot(212)
plt.plot(Lt,Lv,'k--')
plt.savefig("SHM-1.png")
plt.close()
# coding=Big5
from visual import *
def ruler():
X=arrow(pos=(-2,0,0), axis=(4,0,0), shaftwidth=0.03)
L=20
for i in range(-L,L+1):
x=0.1*i
if(i%10==0):
k=2
label(pos=(x,-0.2,0),text='%2d' % int(x),height=20,color=(0,0,0),box=False)
else: k=1
arrow(pos=(x,0,0),axis=(0,0.2*k,0),shaftwidth=0.02)
x0=1.; k=10.; m=1.; w=sqrt(k/m); T=2.*pi/w; A=x0
x1,v1=x0,0.
x2,v2=x0,0.
scene=display(width=800,height=800,center=(0,0,0),background=(0.5,0.5,0))
ball1=sphere(pos=(x0,0,0),radius =0.05,color=(0,0,0))
ball2=sphere(pos=(x0,0,0),radius =0.1,color=color.blue,opacity=0.2)
ruler()
t,dt=0.,0.01
while (t<10.):
t+=dt
rate(int(1./dt)/2)
#C=0----------------
v1+=-k/m*x1*dt
x1+=v1*dt
ball1.pos.x=x1
#有阻尼C=0.002----------------
v2+=-k/m*x2*dt-0.002*v2*dt
x2+=v2*dt
ball2.pos.x=x2
import matplotlib
import matplotlib.pyplot as plt
matplotlib.use("Agg")
import numpy as np
x0=1.; k=10.; m=1.
w=np.sqrt(k/m); T=2.*np.pi/w; A=x0; gamma=0.05
x1,x2,v1,v2=x0,x0,0.,0
t=0.; dt=0.1; Lt=[]; Lx1=[]; Lx2=[]; Lv1=[]; Lv2=[]
while (t < 5.):
Lt.append(t)
Lx1.append(x1); Lv1.append(v1)
Lx2.append(x2); Lv2.append(v2)
t+=dt
v1+=-k/m*x1*dt
x1+=v1*dt
v2+=-k/m*x2*dt-gamma*v2
x2+=v2*dt
plt.subplot(211)
plt.plot(Lt,Lx1,'r-', label=r"$\gamma=0$")
plt.plot(Lt,Lx2,'bo', label=r"$\gamma=0.05$")
plt.legend()
plt.subplot(212)
plt.plot(Lt,Lv1,'r-', label=r"$\gamma=0$")
plt.plot(Lt,Lv2,'bo', label=r"$\gamma=0.05$")
plt.legend()
plt.savefig("SHM-2.png")
plt.close()

# coding=Big5
from visual import *
def ruler():
X=arrow(pos=(-2,0,0), axis=(4,0,0), shaftwidth=0.03)
L=20
for i in range(-L,L+1):
x=0.1*i
if(i%10==0):
k=2
label(pos=(x,-0.2,0),text='%2d' % int(x),height=20,color=(0,0,0),box=False)
else: k=1
arrow(pos=(x,0,0),axis=(0,0.2*k,0),shaftwidth=0.02)
x10=-0.5; k1=20.; m1=10.; L1=1.; xwall=-2.
x20=0.; k2=2.0; m2=1. ; L2=1.
x1,v1=x10,0.
x2,v2=x20,0.
x3,v3=x10,0.
scene=display(width=800,height=800,center=(0,0,0),background=(0.5,0.5,0))
ball1=sphere(pos=(x10,0,0),radius =0.1,color=(0,0,0))
ball2=sphere(pos=(x20,0,0),radius =0.05,color=color.blue)
ball3=sphere(pos=(x10,1,0),radius =0.1,color=(0,0,0))
sp1=helix(pos=(xwall,0,0),axis=(x10-xwall,0,0),radius=0.05,thickness=0.03,color=(1,0,0))
sp2=helix(pos=(x10,0,0),axis=(x20-x10,0,0),radius=0.05,thickness=0.03,color=(1,0,0))
sp3=helix(pos=(xwall,1,0),axis=(x10,0,0),radius=0.05,thickness=0.03,color=(1,0,0))
ruler()
C1=0.01; C2=0.1
t,dt=0.,0.001
while (t<1000.):
t+=dt
rate(int(1./dt)*3)
#C=0----------------
v1+=(-k1*(x1-xwall-L1)+k2*(x2-x1-L2)-C1*v1)/m1*dt
x1+=v1*dt
ball1.pos.x=x1
sp1.axis=vector(x1-xwall,0,0)
v2+=(-k2*(x2-x1-L2)-C2*v2)/m2*dt
x2+=v2*dt
sp2.pos=vector(x1,0,0)
sp2.axis=vector(x2-x1,0,0)
ball2.pos.x=x2
v3+=(-k1*(x3-xwall-L1)-C1*v3)/m1*dt
x3+=v3*dt
ball3.pos.x=x3
sp3.axis=vector(x3-xwall,0,0)
import matplotlib
import matplotlib.pyplot as plt
matplotlib.use("Agg")
import numpy as np
x10=-0.5; k1=20.; m1=10.; L1=1.; xwall=-2.
x20=0.; k2=2.0; m2=1. ; L2=1.
x1,v1=x10,0.
x2,v2=x20,0.
x3,v3=x10,0.
C1=0.01; C2=0.1
t=0.; dt=0.01;
Lt=[]; Lx1=[]; Lx3=[]; Lv1=[]; Lv3=[]
LE1=[]; LE3=[]
while (t < 20.):
print ('%10.4f'*6 %(t,x1,x2,x3,v1**2,v3**2))
Lt.append(t)
Lx1.append(x1); Lv1.append(v1)
Lx3.append(x3); Lv3.append(v3)
LE1.append(v1**2);LE3.append(v3**2)
t+=dt
v1+=(-k1*(x1-xwall-L1)+k2*(x2-x1-L2)-C1*v1)/m1*dt
x1+=v1*dt
v2+=(-k2*(x2-x1-L2)-C2*v2)/m2*dt
x2+=v2*dt
v3+=(-k1*(x3-xwall-L1)-C1*v3)/m1*dt
x3+=v3*dt
plt.subplot(211)
plt.plot(Lt,Lx1,'b--', label="coupled")
plt.plot(Lt,Lx3,'r-', label="non-coupled")
plt.legend()
plt.subplot(212)
plt.plot(Lt,LE1,'b--', label="coupled")
plt.plot(Lt,LE3,'r-', label="non-coupled$")
plt.legend()
plt.savefig("SHM-3.png")
plt.close()