運動的差分近似(Euler method) \[ \vec{r}(t+dt) \simeq \vec{r}(t)+\vec{v}(t)dt \] \[ \vec{v}(t+dt) \simeq \vec{v}(t)+\vec{a}(t)dt \] 為了簡化我們整個物理問題的公式形式,我們要選擇一個恰當的單位系統,如果將軌道運動視為一個圓週運動,那麼我們可以根據圓週運動的向心加速度的公式和週期的公式得到下面的結果: \[\frac{4\pi^2 m r}{T^2}=\frac{GM_s m}{r^2},\]
 \[\frac{1^3}{1^2}=\frac{GM_s}{4\pi^2}, \,\,\, GM_s=4\pi^2\]
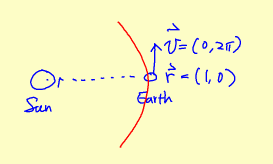
因此在這個單位系統中\(GM_s=4\pi^2\),地球在某一個時刻的坐標為\(\vec{r}=(1,0)\),而這個時刻的速度為\(\vec{v}=(0,2\pi) \,\, v=\frac{2\pi r}{T}=\frac{2\pi \cdot 1}{1}=2\pi\)。
\[\frac{1^3}{1^2}=\frac{GM_s}{4\pi^2}, \,\,\, GM_s=4\pi^2\]
因此在這個單位系統中\(GM_s=4\pi^2\),地球在某一個時刻的坐標為\(\vec{r}=(1,0)\),而這個時刻的速度為\(\vec{v}=(0,2\pi) \,\, v=\frac{2\pi r}{T}=\frac{2\pi \cdot 1}{1}=2\pi\)。
import matplotlib
import matplotlib.pyplot as plt
matplotlib.use("Agg")
import numpy as np
m=1.0; GM=4.*np.pi**2
R0=1.; V0=np.pi*2.
r1=np.array([R0,0.])
v1=np.array([0., V0])
r1n=np.linalg.norm(r1)
a1=np.array([-GM/r1n**3*r1[0],-GM/r1n**3*r1[1]])
xp1=[r1[0]]; yp1=[r1[1]]
t=0.; dt=0.01
tp=[t]
while t < 2.:
print ('%11.5f'*6 %(t,r1[0],r1[1],v1[0],v1[1],r1n))
#print '%9.4f'*7 %(t,dr,drx,r1[0],r1[1],r2[0],r2[1])
v1n=np.linalg.norm(v1)
r1n=np.linalg.norm(r1)
a1=np.array([-GM/r1n**3*r1[0],-GM/r1n**3*r1[1]])
r1+=v1*dt #Euler
v1+=a1*dt
#r1+=v1*dt #Euler-Cromer
t+=dt
tp.append(t)
xp1.append(r1[0])
yp1.append(r1[1])
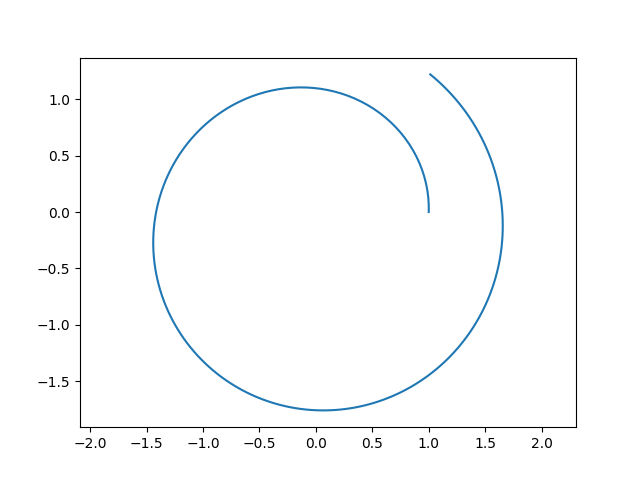
plt.plot(xp1,yp1)
plt.axis('equal')
plt.savefig("orbital-1.png")
plt.close()
# coding=Big5
import numpy as np
import matplotlib.pyplot as plt
m=1.0; GM=4.*np.pi**2
R0=1.; V0=np.pi*2.
r1=np.array([R0,0.])
v1=np.array([0., V0])
r1n=np.linalg.norm(r1)
a1=np.array([-GM/r1n**3*r1[0],-GM/r1n**3*r1[1]])
xp1=[r1[0]]; yp1=[r1[1]]
r2=np.array([R0,0.])
v2=np.array([0., V0*0.8])
r2n=np.linalg.norm(r2)
a2=np.array([-GM/r2n**3*r2[0],-GM/r2n**3*r2[1]])
xp2=[r2[0]]; yp2=[r2[1]]
t=0.; dt=0.01
tp=[t]
while t < 2.:
print '%10.5f'*7 %(t,r1[0],r1[1],r2[0],r2[1],r1n,r2n)
#print '%9.4f'*7 %(t,dr,drx,r1[0],r1[1],r2[0],r2[1])
v1n=np.linalg.norm(v1)
r1n=np.linalg.norm(r1)
a1=np.array([-GM/r1n**3*r1[0],-GM/r1n**3*r1[1]])
r1+=v1*dt
v1+=a1*dt
#r1+=v1*dt
v2n=np.linalg.norm(v2)
r2n=np.linalg.norm(r2)
a2=np.array([-GM/r2n**3*r2[0],-GM/r2n**3*r2[1]])
r2+=v2*dt
v2+=a2*dt
#r2+=v2*dt
t+=dt
tp.append(t)
xp1.append(r1[0]); yp1.append(r1[1])
xp2.append(r2[0]); yp2.append(r2[1])
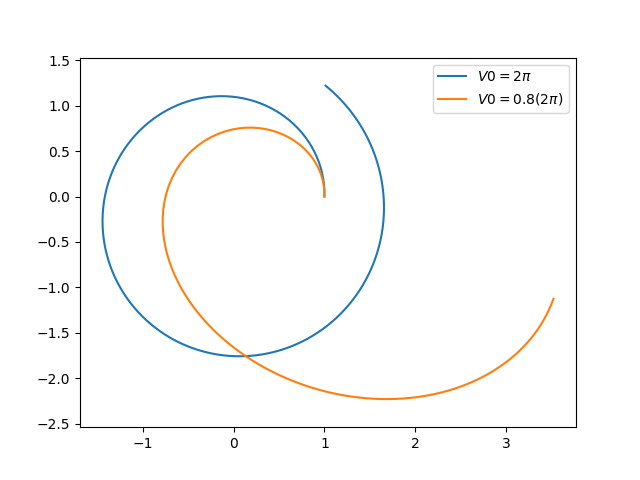
plt.plot(xp1,yp1)
plt.axis('equal')
plt.plot(xp2,yp2)
plt.show()
那麼這樣的順序是對的,因為r1的更新時所使用的速度v1,就是時間為t的時候的速度;v1更新時所使用的加速度,也是在時間為t的時候的加速度a1。Euler-Cromer method是將位置的更新與速度的更新的兩條指令對調:a1=np.array([-GM/r1n**3*r1[0],-GM/r1n**3*r1[1]]) r1+=v1*dt v1+=a1*dt
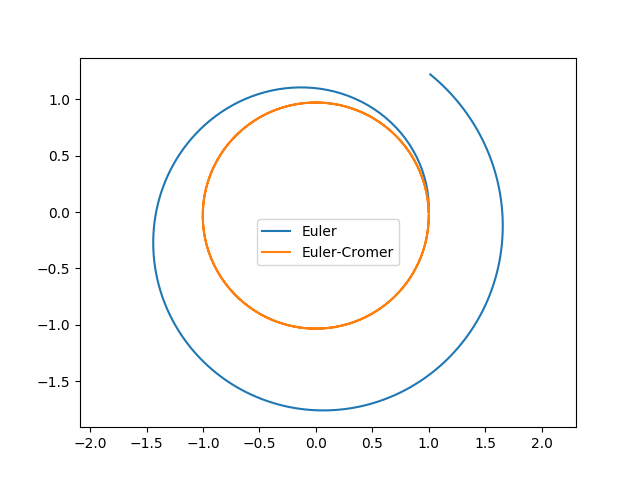
如此一來雖然速度v1的更新,仍然是使用前一個時刻的加速度a1,但是位置r1的更新,所使用的速度並前一時刻的速度,而是已經更新過後的速度。所以如果我們的數值計算是用這種方式來進行的話,那麼將是兩種更新的混合。原則上我們並不知道哪一個方式會得到比較精確的結果,但是在實際應用中,似乎Euler-Cromer method都具有較高的精確度,例如下面的樣本程式就是比較Euler和Euler-Cromer計算一個行星運動的程式,我們從這個程式執行得到的數據作比較,可以明顯發現Euler-Cromer確實有相當大幅度的改進。a1=np.array([-GM/r1n**3*r1[0],-GM/r1n**3*r1[1]]) v1+=a1*dt r1+=v1*dt
import matplotlib
import matplotlib.pyplot as plt
matplotlib.use("Agg")
import numpy as np
m=1.0; GM=4.*np.pi**2
R0=1.; V0=np.pi*2.
r1=np.array([R0,0.])
v1=np.array([0., V0])
r1n=np.linalg.norm(r1)
a1=np.array([-GM/r1n**3*r1[0],-GM/r1n**3*r1[1]])
xp1=[r1[0]]; yp1=[r1[1]]
r2=np.array([R0,0.])
v2=np.array([0., V0*1.])
r2n=np.linalg.norm(r2)
a2=np.array([-GM/r2n**3*r2[0],-GM/r2n**3*r2[1]])
xp2=[r2[0]]; yp2=[r2[1]]
t=0.; dt=0.01
tp=[t]
while t < 2.:
print ('%10.5f'*7 %(t,r1[0],r1[1],r2[0],r2[1],r1n,r2n))
v1n=np.linalg.norm(v1)
r1n=np.linalg.norm(r1)
a1=np.array([-GM/r1n**3*r1[0],-GM/r1n**3*r1[1]])
r1+=v1*dt
v1+=a1*dt
#r1+=v1*dt
v2n=np.linalg.norm(v2)
r2n=np.linalg.norm(r2)
a2=np.array([-GM/r2n**3*r2[0],-GM/r2n**3*r2[1]])
#r2+=v2*dt
v2+=a2*dt
r2+=v2*dt
t+=dt
tp.append(t)
xp1.append(r1[0]); yp1.append(r1[1])
xp2.append(r2[0]); yp2.append(r2[1])
plt.plot(xp1,yp1,label=r"Euler")
plt.plot(xp2,yp2,label=r"Euler-Cromer")
plt.axis('equal')
plt.legend()
plt.savefig("orbital-3.png")
plt.close()
- 對單一一個微分方程\[\frac{dx}{dt}=f(x,t)\] RK2的做法如下:\[x(t+\tau)=x(t)+\tau f^*(x^*,t^*)\]
- 在自由落體運動中 我們已經使用過RK2的方法,其中面臨有兩個微分方程式需要處理,一個是位置(\(\frac{dy}{dt}=v\))另外一個是速度(\(\frac{dv}{dt}=a\)),所使用的公式如下:
- 對於現在我們要處理的行星軌道運動問題, 基本上也是有兩個微分方程,位置與速度兩個微分方程,但是更複雜的是行星在平面上運動,每一個方程式都有兩個分量(x,y,vx,vy),因此RK2的公式應為: \[ \vec{r}(t+\tau)=\vec{r}(t) + \tau \vec{v}^*\] \[ \vec{v}(t+\tau)=\vec{v}(t) + \tau \vec{a}^*\] 其中的中介速度與加速度向量為 \[ \vec{r}^*=\vec{r}(t) + \frac{\tau}{2}\vec{v}(t) \] \[ \vec{v}^*=\vec{v}(t) + \frac{\tau}{2}\vec{a}(t) \] \[ \vec{a}^*=\vec{a}(t^*, \vec{r}^*, \vec{v}^*)=-\frac{GM_s}{{r^*}^3}\vec{r}^* \] \[t^*=t+\tau/2\]
根據RK2的原理,首先要算出在\(t^*=t+dt/2\)的\[y^*=y(t)+v(t)*dt/2,\] \[ v^*=v(t)+a(t)*dt/2,\] \[ a^*=a(t^*,v^*)=g-b/m*v^*\],再利用這些中介的數據求取新的位置與速度: \[y(t+dt)+=v^**dt,\] \[ v(t+dt)+=a^**dt \] \[t^*=t+\tau/2\]
import matplotlib
import matplotlib.pyplot as plt
matplotlib.use("Agg")
import numpy as np
m=1.0; GM=4.*np.pi**2
R0=1.; V0=np.pi*2.
r1=np.array([R0,0.])
v1=np.array([0., V0])
r1n=np.linalg.norm(r1)
a1=np.array([-GM/r1n**3*r1[0],-GM/r1n**3*r1[1]])
xp1=[r1[0]]; yp1=[r1[1]]
r2=np.array([R0,0.])
v2=np.array([0., V0*1.])
r2n=np.linalg.norm(r2)
a2=np.array([-GM/r2n**3*r2[0],-GM/r2n**3*r2[1]])
xp2=[r2[0]]; yp2=[r2[1]]
t=0.; dt=0.01; dt2=dt/2.
tp=[t]
while t < 2.:
print ('%10.5f'*7 %(t,r1[0],r1[1],r2[0],r2[1],r1n,r2n))
v1n=np.linalg.norm(v1)
r1n=np.linalg.norm(r1)
a1=np.array([-GM/r1n**3*r1[0],-GM/r1n**3*r1[1]])
r1+=v1*dt
v1+=a1*dt
#r1+=v1*dt
v2n=np.linalg.norm(v2)
r2n=np.linalg.norm(r2)
a2=np.array([-GM/r2n**3*r2[0],-GM/r2n**3*r2[1]])
ts=+dt2
r2s=r2+v2*dt2
v2s=v2+a2*dt2
r2sn=np.linalg.norm(r2s)
a2s=np.array([-GM/r2sn**3*r2s[0],-GM/r2sn**3*r2s[1]])
r2+=v2s*dt
v2+=a2s*dt
#r2+=v2*dt
t+=dt
tp.append(t)
xp1.append(r1[0]); yp1.append(r1[1])
xp2.append(r2[0]); yp2.append(r2[1])
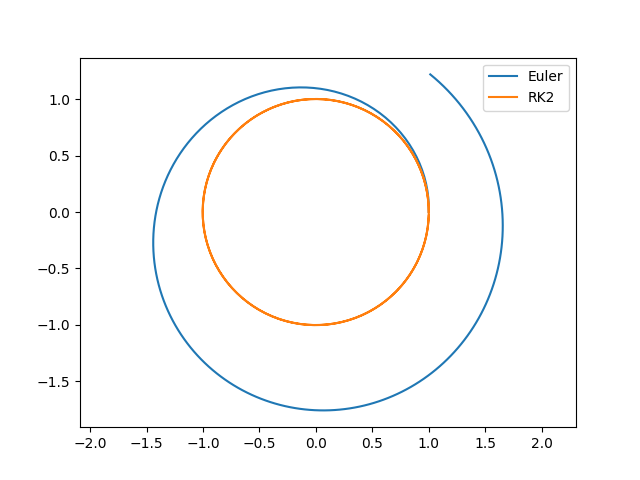
plt.plot(xp1,yp1,label=r"Euler")
plt.plot(xp2,yp2,label=r"RK2")
plt.axis('equal')
plt.legend()
plt.savefig("orbital-4.png")
plt.close()