Runge-Kutta 4th order method
-
Runge-Kutta 4th order公式
-
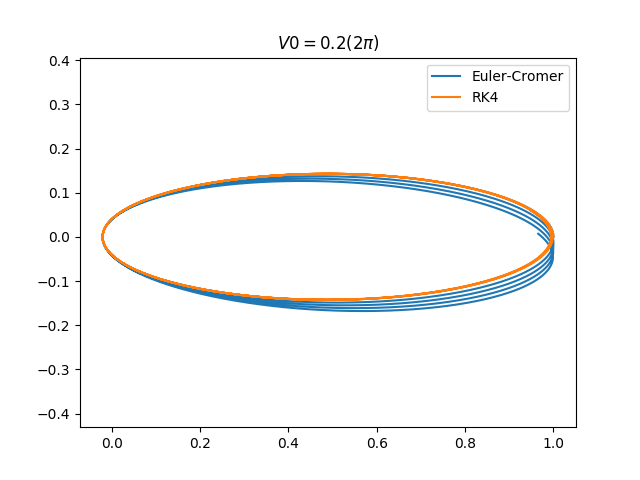
RK4在軌道運動中的應用
在軌道運動中的RK4方程式 -
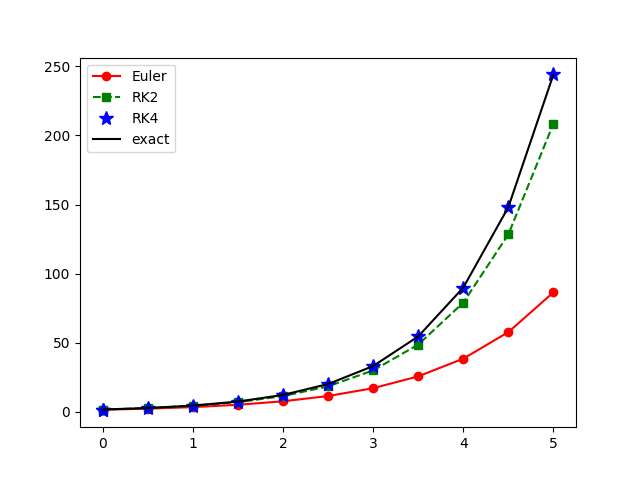
4個數值方法之比較
微分方程:\[ \frac{dx}{dt}=f(x(t),t) \] Euler method: \[ x(t+\tau)=x(t)+\tau f(x(t),t) \] RK2 method: \[ x(t+\tau)=x(t)+\tau \textstyle f(x^*(t+\frac{1}{2}\tau),t+\frac{1}{2}\tau) \] \[ x^*(t+\textstyle\frac{1}{2}\tau)=x(t)+\frac{1}{2}\tau f(x(t),t) \] RK4 method: \[ x(t+\tau)=x(t)+\textstyle \frac{1}{6}\tau[F_1 + 2F_2 + 2F_3 + F_4] \] \[F_1=f(x,t) \] \[F_2=f(x+\textstyle \frac{1}{2}\tau F_1,t+\frac{1}{2}\tau) \] \[F_3=f(x+\textstyle \frac{1}{2}\tau F_2,t+\frac{1}{2}\tau) \] \[F_4=f(x+\tau F_3,t+\tau) \]
import matplotlib
import matplotlib.pyplot as plt
matplotlib.use("Agg")
import numpy as np
def deriv(t,x):
f=x
return f
def exact(t):
x=np.exp(t)
return x
N=10
a,b=0.,5.
dt=(b-a)/N
t,x1,x2,x3=a,1.,1.,1.
xe=exact(t)
tp=[t]; x1p=[x1]; x2p=[x2]; x3p=[x3]; xep=[xe]
for i in range(N+1):
xe=exact(t)
print ('%6.3f %12.7f %12.7f %12.7f %12.7f' %(t,x1,x2,x3,xe))
#------Euler
x1+=deriv(t,x1)*dt
#-------RK2
ts=t+0.5*dt
xs=x2+0.5*dt*deriv(t,x2)
x2+=deriv(ts,xs)*dt
#-------RK4
ts=t+0.5*dt
F1=deriv(t,x3)
F2=deriv(ts,x3+0.5*dt*F1)
F3=deriv(ts,x3+0.5*dt*F2)
F4=deriv(t+dt,x3+dt*F3)
x3+=(1./6.)*dt*(F1+2.*F2+2.*F3+F4)
tp.append(t)
x1p.append(x1)
x2p.append(x2)
x3p.append(x3)
xep.append(xe)
t+=dt
plt.plot(tp,x1p,'r-o',label='Euler')
plt.plot(tp,x2p,'g--s',label='RK2')
plt.plot(tp,x3p,'b*',ms=10,label='RK4',)
plt.plot(tp,x3p,'k-',label='exact')
plt.title(r"$\frac{dx}{dt}=x$")
plt.legend()
plt.savefig("RK4-1.png")
plt.close()
import matplotlib
import matplotlib.pyplot as plt
matplotlib.use("Agg")
import numpy as np
def gravrk(s,t,GM):
r = np.array([s[0], s[1]])
v = np.array([s[2], s[3]])
accel = -GM*r/np.linalg.norm(r)**3 # Gravitational acceleration
deriv = np.array([v[0], v[1], accel[0], accel[1]])
return deriv
def rk4(x,t,tau,derivsRK,param):
half_tau = 0.5*tau
F1 = derivsRK(x,t,param)
t_half = t + half_tau
xtemp = x + half_tau*F1
F2 = derivsRK(xtemp,t_half,param)
xtemp = x + half_tau*F2
F3 = derivsRK(xtemp,t_half,param)
t_full = t + tau
xtemp = x + tau*F3
F4 = derivsRK(xtemp,t_full,param)
xout = x + tau/6.*(F1 + F4 + 2.*(F2+F3))
return xout
m=1.0; GM=4.*np.pi**2
R0=1.; V0=np.pi*2.0*0.2
r1=np.array([R0,0.])
v1=np.array([0., V0])
r1n=np.linalg.norm(r1)
a1=np.array([-GM/r1n**3*r1[0],-GM/r1n**3*r1[1]])
xp1=[r1[0]]; yp1=[r1[1]]
r2=np.array([R0,0.])
v2=np.array([0., V0*1.])
r2n=np.linalg.norm(r2)
a2=np.array([-GM/r2n**3*r2[0],-GM/r2n**3*r2[1]])
xp2=[r2[0]]; yp2=[r2[1]]
t=0.; dt=0.0001; dt2=dt/2.
tp=[t]
while t < 1.5:
#print '%10.5f'*7 %(t,r1[0],r1[1],r2[0],r2[1],r1n,r2n)
v1n=np.linalg.norm(v1)
r1n=np.linalg.norm(r1)
a1=np.array([-GM/r1n**3*r1[0],-GM/r1n**3*r1[1]])
#r1+=v1*dt
v1+=a1*dt
r1+=v1*dt
state=np.array([r2[0],r2[1],v2[0],v2[1]])
state = rk4(state,t,dt,gravrk,GM)
r2[0]=state[0]
r2[1]=state[1]
v2[0]=state[2]
v2[1]=state[3]
t+=dt
tp.append(t)
xp1.append(r1[0]); yp1.append(r1[1])
xp2.append(r2[0]); yp2.append(r2[1])
plt.plot(xp1,yp1, label="Euler-Cromer")
plt.axis('equal')
plt.plot(xp2,yp2, label="RK4")
plt.title(r"$V0=0.2(2\pi)$")
plt.legend()
plt.savefig("RK4-2.png")
plt.close()
from visual import *
import numpy as np
import matplotlib.pyplot as plt
#* Define the gravrk function used by the Runge-Kutta routines
def gravrk(s,t,GM):
r = np.array([s[0], s[1]])
v = np.array([s[2], s[3]])
accel = -GM*r/np.linalg.norm(r)**3 # Gravitational acceleration
deriv = np.array([v[0], v[1], accel[0], accel[1]])
return deriv
def Euler(x,t,tau,derivsRK,param):
F1 = derivsRK(x,t,param)
xout = x + tau*F1
return xout
def rk4(x,t,tau,derivsRK,param):
half_tau = 0.5*tau
F1 = derivsRK(x,t,param)
t_half = t + half_tau
xtemp = x + half_tau*F1
F2 = derivsRK(xtemp,t_half,param)
xtemp = x + half_tau*F2
F3 = derivsRK(xtemp,t_half,param)
t_full = t + tau
xtemp = x + tau*F3
F4 = derivsRK(xtemp,t_full,param)
xout = x + tau/6.*(F1 + F4 + 2.*(F2+F3))
return xout
x0=1.; v0=1.0; G=1.; Ms=4.*pi**2; GM=G*Ms
scene = display(width=800, height=800, center=(0, 0, 0),
background=(0.5,0.5,0))
planet=sphere(pos=(x0,0,0),radius =0.05,color=(0,0,0),
make_trail=True, trail_type="points", interval=1, retain=100)
sun=sphere(pos=(0,0,0),radius =0.02,color=(1,1,0))
from visual.graph import * # import graphing features
gd = gdisplay(x=800,y=0,width=600, height=600,
title='y(x) as a solution of ODE: dx/dt=x', xtitle='t', ytitle='x',
foreground=color.black, background=color.white
,xmin=-1, xmax=1, ymin=-1, ymax=1)
f = gdots(gdisplay=gd,color=color.black)
planet.v=vector(0,v0*pi,0.)
dt=0.001; dt2=dt/2.
t=0.
while True:
if(t > 1.7): break
rate(int(1./dt)/5)
f.plot(pos=(planet.x,planet.y))
state = np.array([ planet.pos.x, planet.pos.y, planet.v.x, planet.v.y ])
#----Euler
#state = Euler(state,t,dt,gravrk,GM)
#----RK4
state = rk4(state,t,dt,gravrk,GM)
planet.pos.x=state[0]
planet.pos.y=state[1]
planet.v.x=state[2]
planet.v.y=state[3]
t=t+dt
from visual import *
import numpy as np
import matplotlib.pyplot as plt
#* Define the gravrk function used by the Runge-Kutta routines
def gravrk(s,t,GM):
r = np.array([s[0], s[1]]) # Unravel the vector s into position and velocity
v = np.array([s[2], s[3]])
accel = -GM*r/np.linalg.norm(r)**3 # Gravitational acceleration
deriv = np.array([v[0], v[1], accel[0], accel[1]])
return deriv
def rk2(x,t,tau,derivsRK,param):
half_tau = 0.5*tau
F1 = derivsRK(x,t,param)
xtemp=x+half_tau*F1
t_half = t + half_tau
F2=derivsRK(xtemp,t_half,param)
xout = x + tau*F2
return xout
def rk4(x,t,tau,derivsRK,param):
half_tau = 0.5*tau
F1 = derivsRK(x,t,param)
t_half = t + half_tau
xtemp = x + half_tau*F1
F2 = derivsRK(xtemp,t_half,param)
xtemp = x + half_tau*F2
F3 = derivsRK(xtemp,t_half,param)
t_full = t + tau
xtemp = x + tau*F3
F4 = derivsRK(xtemp,t_full,param)
xout = x + tau/6.*(F1 + F4 + 2.*(F2+F3))
return xout
x0=1.; v0=1.0; G=1.; Ms=4.*pi**2; GM=G*Ms
scene = display(width=800, height=800, center=(0, 0, 0),
background=(0.5,0.5,0))
planet1=sphere(pos=(x0,0,0),radius =0.05,color=(1,0,0),
make_trail=True)
planet2=sphere(pos=(x0,0,0),radius =0.05,color=(0,1,0),
make_trail=True)
planet3=sphere(pos=(x0,0,0),radius =0.05,color=(0,0,1),
make_trail=True,trail_type="points", interval=1, retain=100)
planet4=sphere(pos=(x0,0,0),radius =0.05,color=(0,0,0),
make_trail=True,trail_type="points", interval=1, retain=50)
sun=sphere(pos=(0,0,0),radius =0.02,color=(1,1,0))
from visual.graph import * # import graphing features
gd = gdisplay(x=800,y=0,width=600, height=600,
title='y(x) as a solution of ODE: dx/dt=x', xtitle='t', ytitle='x',
foreground=color.black, background=color.white
,xmin=-1, xmax=1, ymin=-1, ymax=1)
f1 = gcurve(gdisplay=gd,color=color.red) # a graphics curve
f2 = gdots(gdisplay=gd,color=color.green)
f3 = gdots(gdisplay=gd,color=color.blue)
f4 = gdots(gdisplay=gd,color=color.black)
planet1.v=vector(0,v0*pi,0.)
planet2.v=vector(0,v0*pi,0.)
planet3.v=vector(0,v0*pi,0.)
planet4.v=vector(0,v0*pi,0.)
dt=0.002; dt2=dt/2.
t=0.
while True:
if(t > 1.7): break
rate(int(1./dt)/10)
f1.plot(pos=(planet1.x,planet1.y))
f2.plot(pos=(planet2.x,planet2.y))
f3.plot(pos=(planet3.x,planet3.y))
f4.plot(pos=(planet4.x,planet4.y))
#-----Euler
planet1.a=-G*Ms/(abs(planet1.pos)**3)*planet1.pos
v0=1.*planet1.v
planet1.v+=planet1.a*dt
if(abs(planet1.pos)<1.2): planet1.pos+=v0*dt
#-----Euler-Cromer
planet2.a=-G*Ms/(abs(planet2.pos)**3)*planet2.pos
planet2.v+=planet2.a*dt
planet2.pos+=planet2.v*dt
#----RK4
state = np.array([ planet3.pos.x, planet3.pos.y, planet3.v.x, planet3.v.y ])
state = rk4(state,t,dt,gravrk,GM)
planet3.pos.x=state[0]
planet3.pos.y=state[1]
planet3.v.x=state[2]
planet3.v.y=state[3]
#----RK2
#a1=-G*Ms/(abs(planet3.pos)**3)*planet3.pos
#rs=planet3.pos+planet3.v*dt2
#vs=planet3.v-a1*dt2
#am=-G*Ms/(abs(rs)**3)*rs
#planet3.pos+=planet3.v*dt
#planet3.v+=am*dt
state = np.array([ planet4.pos.x, planet4.pos.y, planet4.v.x, planet4.v.y ])
state = rk2(state,t,dt,gravrk,GM)
planet4.pos.x=state[0]
planet4.pos.y=state[1]
planet4.v.x=state[2]
planet4.v.y=state[3]
t=t+dt