計算物理: 拋體運動
在這個單元當中我們要用三維差分近似模擬拋體運動。
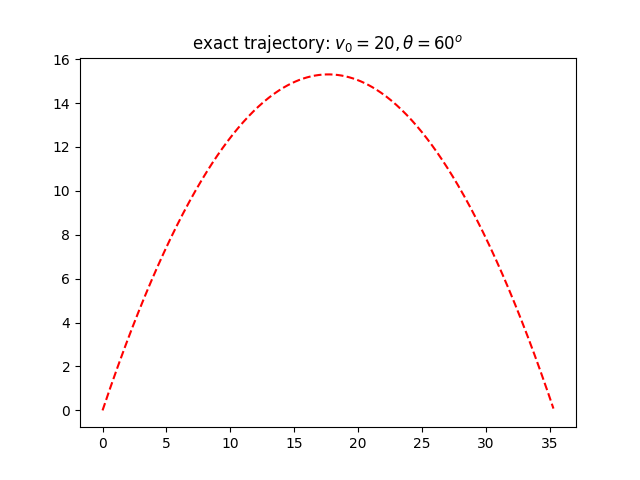
拋體運動之精確解
拋體運動之精確解如下:\[ x(t)=v_0 \cos(\theta) t, \] \[ y(t)=v_0 \sin(\theta) t-\frac{1}{2} g t^2 \] 物體在xy-平面中運動的時候,它所受到的力量是一個向量,所以加速度向量,速度向量和位置向量的更新都必須考慮2個分量。
拋體運動
import matplotlib
import matplotlib.pyplot as plt
matplotlib.use("Agg")
import numpy as np
degree=60.; theta=np.radians(degree)
g=-9.8; v0=20.; (x,y)=(0,0)
vx0=v0*np.cos(theta)
vy0=v0*np.sin(theta)
tf=2.*vy0/abs(g)
et=np.arange(0,tf,0.01)
ex=vx0*et
ey=vy0*et+0.5*g*et**2
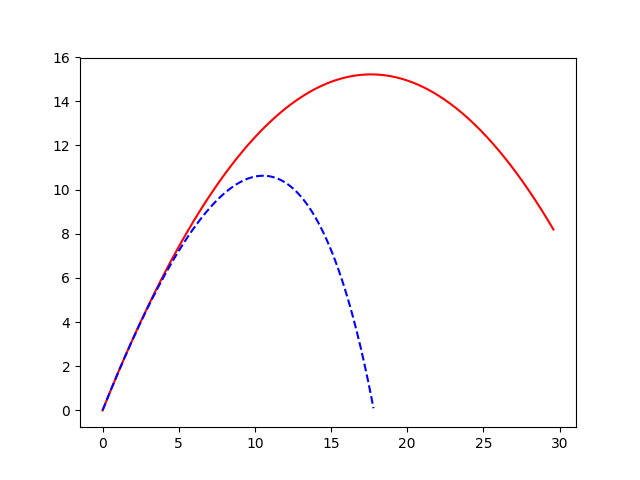
plt.plot(ex,ey,'r--')
plt.title('exact trajectory: '+r'$v_0=20, \theta=60^o$')
plt.savefig("projectile-exact.png")
動畫模擬1
# coding=Big5
from visual import *
vx,vy=10.,20.
scene = display(width=800, height=800, center=(20, 10, 0),
background=(0.5,0.5,0))
floor=box(pos=(20,0,0),size=(60,0.1,40), color=color.cyan)
ball1 = sphere(pos=(0,0,0),radius =0.3,make_trail=True,color=(0,0,0))
t,dt=0.,0.01
while True:
if( ball1.pos.y < 0.): break
rate(int(1./dt)/2)
ball1.pos=vector(vx*t,vy*t-0.5*9.8*t**2)
t+=dt
3維運動之差分近似
運動方程式的差分近似: \[ \vec{v}(t+dt)=\vec{v}(t)+\vec{a}dt \] \[ \vec{x}(t+dt)=\vec{x}(t)+\vec{v}dt \] 物體在三維空間中運動的時候,它所受到的力量是一個向量,所以加速度向量,速度向量和位置向量的更新都必須考慮三個分量。
import matplotlib
import matplotlib.pyplot as plt
matplotlib.use("Agg")
import numpy as np
degree=60.; theta=np.radians(degree)
g=-9.8; v0=20.; (x,y)=(0,0)
vx0=v0*np.cos(theta)
vy0=v0*np.sin(theta)
vx=vx0; vy=vy0
t=0.; dt=0.1; Lt=[]; Lx=[]; Ly=[]
while True:
if(y < 0.): break
print ('%10.4f'*3 %(t,x,y))
vy+=g*dt
x+=vx*dt
y+=vy*dt
Lt.append(t)
Lx.append(x)
Ly.append(y)
t+=dt
tf=tf=2.*vy0/abs(g)
et=np.arange(0,tf,0.01)
ex=vx0*et
ey=vy0*et+0.5*g*et**2
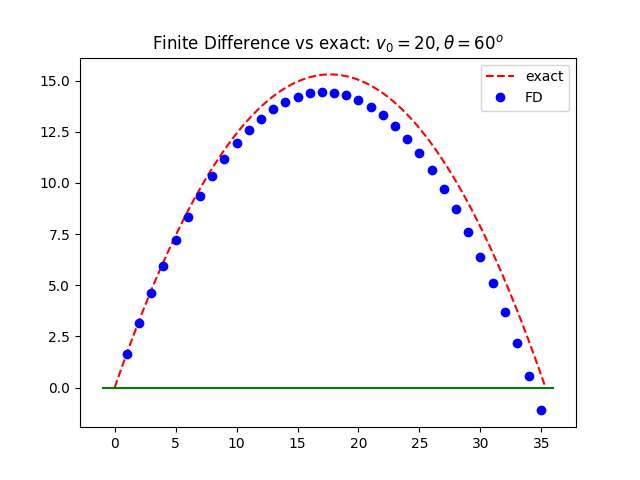
plt.plot(ex,ey,'r--', label="exact")
plt.plot(Lx,Ly,'bo', label="FD")
plt.plot([-1,x+1],[0,0],'g-')
plt.legend()
plt.title('Finite Difference vs exact: '+r'$v_0=20, \theta=60^o$')
plt.savefig("projectile.png")
Use vector with np.array
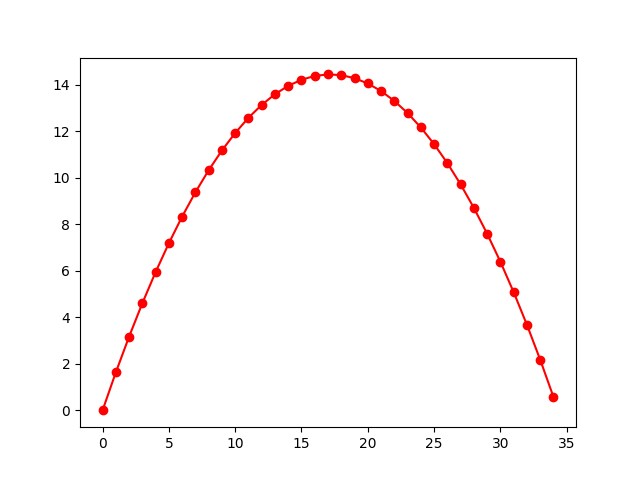
import matplotlib
import matplotlib.pyplot as plt
matplotlib.use("Agg")
import numpy as np
g=-9.8; degree=60.; theta=np.radians(degree)
v0=20.; vx0=v0*np.cos(theta); vy0=v0*np.sin(theta)
r1=np.array([0.,0.]); v1=np.array([vx0,vy0])
a1=np.array([0., g])
t=0; dt=0.1; x=[]; y=[];
while True:
if( r1[1] < 0.): break
print ('%10.4f'*3 %(t,r1[0],r1[1]))
x.append(r1[0]); y.append(r1[1])
v1+=a1*dt
r1+=v1*dt
t+=dt
tf=2*vy0/abs(g)
R=v0**2*np.sin(theta*2.)/abs(g)
print ("exact:",tf,R)
plt.plot(x,y,'r-o')
plt.savefig("proj-vec.png")
plt.close()
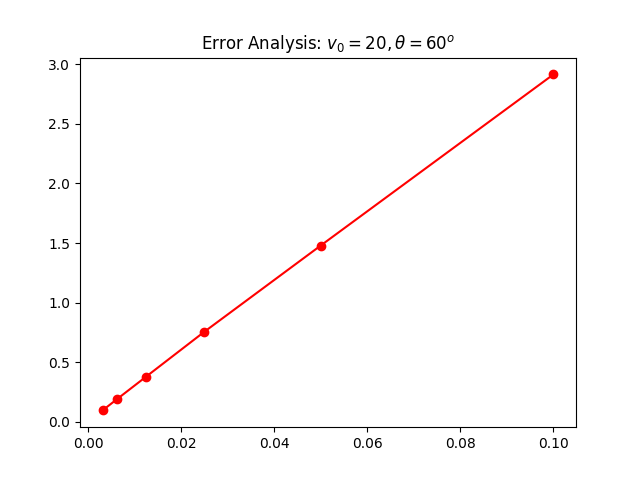
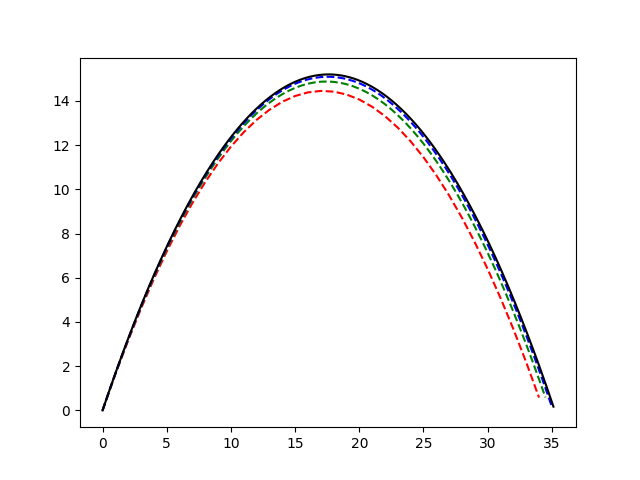
比較精確運動解和差分近似所得的結果差異
差分近似的精確度由微量的時間dt決定,我們可以透過比較 差分近似模擬以及精確運動解來感受微量的時間的影響。
import matplotlib
import matplotlib.pyplot as plt
matplotlib.use("Agg")
import numpy as np
degree=60.; theta=np.radians(degree)
g=-9.8; v0=20.
Ldt=[]; LD=[];
Lx=[[] for i in range(6)]
Ly=[[] for i in range(6)]
for n in range(6):
(x,y)=(0,0)
vx0=v0*np.cos(theta)
vy0=v0*np.sin(theta)
vx=vx0; vy=vy0
dt=0.1/2**n
t=0.; D=0.
while True:
if(y < 0.): break
Lx[n].append(x)
Ly[n].append(y)
xe=vx0*t
ye=vy0*t+0.5*g*t**2
D+=np.sqrt((x-xe)**2+(y-ye)**2)*dt
#print ('%10.4f'*6 %(t,x,y,xe,ye,D))
vy+=g*dt
x+=vx*dt
y+=vy*dt
t+=dt
print ('dt,D=',dt,D)
Ldt.append(dt); LD.append(D)
plt.plot(Ldt,LD,'r-o')
plt.title('Error Analysis: '+r'$v_0=20, \theta=60^o$')
plt.savefig("ErrANA.png")
plt.close()
plt.show()
plt.plot(Lx[0],Ly[0], 'r--')
plt.plot(Lx[1],Ly[1], 'g--')
plt.plot(Lx[2],Ly[2], 'b--')
plt.plot(Lx[3],Ly[3], 'k-')
plt.savefig("ErrANA-1.png")
拋體運動加入空氣阻力
\[\vec{f}=\vec{f}_g+\vec{F}_D=-mg \hat{j}-bv^2 \hat{v} \]
\[\vec{a}=\vec{f}/m=-g\vec{j}-(b/m)v\vec{v} \]
\[ b=1/2 \rho C_D A \]
其中
- \(F_D\) 為阻力
- \(\rho\) 為流體密度
- \(v\) 為流體相對於物體的速度
- \(C_d\) 為阻力係數,為一無因次的參數,像汽車的阻力係數約為0.25至0.45
- \(A\) 為參考面積
與自由落體不同的是阻力由速度向量決定,而速度向量不是在鉛垂方向,而是有x方向的分量。我們在程式中加入了空氣阻力,進而能夠觀察空氣阻力對運動的影響。完成了這個基本的模擬程式之後,考慮不同的阻力係數對運動軌跡的影響。我們會注意到有阻力的情況下,拋體的軌跡不再是完美的拋物線,而是在最高點之後有比較高的傾向呈現自由落體。這也就是為什麼外野手總是能夠順利的接到高飛球。
import matplotlib
import matplotlib.pyplot as plt
matplotlib.use("Agg")
import numpy as np
m=0.1; r=0.2; rho=1.2; Cd=0.5; g=-9.8
A=np.pi*r**2; air_c=0.5*Cd*rho*A/m
degree=60.; theta=np.radians(degree)
v0=20.; vx0=v0*np.cos(theta); vy0=v0*np.sin(theta)
r1=np.array([0.,0.]); v1=np.array([vx0,vy0])
r2=np.array([0.,0.]); v2=np.array([vx0,vy0])
a1=np.array([0., g])
a2=np.array([0., g])-air_c*v2
t,dt=0.,0.01
x1=[];y1=[];x2=[];y2=[]
while True:
if( r2[1] < 0.): break
print ('%10.4f'*5 %(t,r1[0],r1[1],r2[0],r2[1]))
x1.append(r1[0]);y1.append(r1[1])
x2.append(r2[0]);y2.append(r2[1])
v1+=a1*dt
r1+=v1*dt
a2=np.array([0., g])-air_c*v2
v2+=a2*dt
r2+=v2*dt
t+=dt
plt.plot(x1,y1,'r-')
plt.plot(x2,y2,'b--')
plt.savefig("proj-vec-airdrag.png")
plt.close()
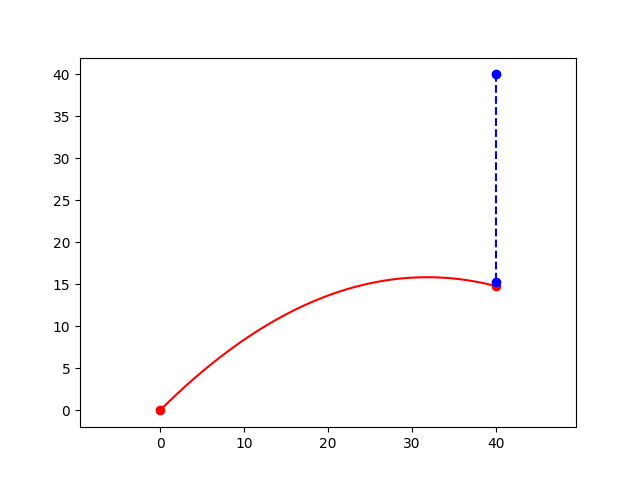
射擊猴子
Shoot the Monkey
在上面的影片中我們可以看見一個砲彈指向一個猴子(自由落體球),砲彈在猴子開始自由落體的瞬間射出,我們可以看見這個炮彈會在空中擊中這個猴子。同學們可以參考下列程式後面實際操作的實驗影片。
# coding=Big5
from visual import *
g=9.8; v0=25.; LX=40.; H=40.
theta=atan(H/LX)
r1=vector(0,0,0)
v1=vector(v0*cos(theta),v0*sin(theta),0)
a1=vector(0, -9.8, 0)
r2=vector(LX,H,0)
v2=vector(0,0.,0)
a2=vector(0, -9.8, 0)
scene = display(width=800, height=800, center=(20, 10, 0),
background=(0.5,0.5,0))
floor=box(pos=(20,0,0),size=(60,0.1,40), color=color.cyan)
ar=arrow(pos=(0,0,0),axis=(LX,H,0),shaftwidth=0.2)
cylinder(pos=(0,0,0),axis=(1,1,0),radius=0.7,color=(1,1,0))
ball1 = sphere(pos=r1,radius =0.5,make_trail=True,color=(0,0,0))
ball2 = sphere(pos=r2,radius = 1,make_trail=True,color=(1,0,0)
,opacity=0.2)
t,dt=0.,0.01
while True:
if( r2.y < 0.): break
if(abs(r2-r1)<0.1): break
rate(50)
v1+=a1*dt
r1+=v1*dt
ball1.pos=r1
v2+=a2*dt
r2+=v2*dt
ball2.pos=r2
t+=dt
import matplotlib
import matplotlib.pyplot as plt
matplotlib.use("Agg")
import numpy as np
g=-9.8; v0=25.; LX=40.; H=40.
theta=np.arctan(H/LX)
vx0=v0*np.cos(theta); vy0=v0*np.sin(theta)
r1=np.array([0.,0.]); v1=np.array([vx0,vy0])
a1=np.array([0., g])
r2=np.array([LX,H]); v2=np.array([0.,0.])
a2=np.array([0., g])
t=0.; dt=0.01; x1=[];y1=[];x2=[];y2=[]
while True:
if( r2[1] < 0.): break
d=np.sqrt((r2[0]-r1[0])**2+(r2[1]-r1[1])**2)
if(d < 0.1): break
x1.append(r1[0]); y1.append(r1[1])
x2.append(r2[0]); y2.append(r2[1])
v1+=a1*dt
r1+=v1*dt
v2+=a2*dt
r2+=v2*dt
t+=dt
x=r1[0]; y=r1[1]
plt.plot(x1,y1,'r-')
plt.plot(x2,y2,'b--')
plt.plot([0,x],[0,y],'ro')
plt.plot([LX,x],[H,y+0.5],'bo')
plt.axis('equal')
plt.savefig("proj-vec-monkey.png")
plt.close()
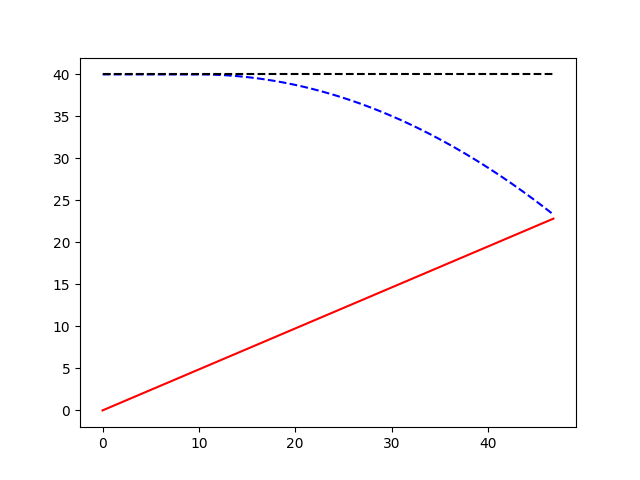
射擊炸彈
Shoot the bomb
上面的影片中呈現出一個飛機在時間t=0.5水平拋出了一個炸彈,有一個砲彈手在t=1.5射擊這個炸彈,砲彈射擊的速度和角度都非常適當,能夠在空中擊中炸彈。下面的程式裡頭的砲彈初速度和砲彈的射擊角度不能夠擊中炸彈,請你反覆執行這個程式,找到適當的砲彈射擊速度和角度,能夠在炸彈落地之前擊中這個炸彈。
# coding=Big5
from visual import *
g=9.8; v0=65.; H=40.
theta=radians(45.)
r1=vector(0,0,0)
v1=vector(v0*cos(theta),v0*sin(theta),0)
a1=vector(0, -9.8, 0)
r3=vector(0,H,0)
v3=vector(20.,0,0)
r2=vector(0,H,0)
v2=vector(20,0,0)
a2=vector(0, -9.8, 0)
scene = display(width=800, height=800, center=(20, 10, 0),
background=(0.5,0.5,0))
floor=box(pos=(20,0,0),size=(60,0.1,40), color=color.cyan)
ball1 = sphere(pos=r1,radius =0.5,make_trail=True,color=(0,0,0))
plane=cylinder(pos=r3,axis=(4,0,0),radius=1)
ball2 = sphere(pos=r2,radius = 1,make_trail=True,color=(1,0,0)
,opacity=0.2)
t,dt=0.,0.01
while True:
if( r1.y < 0.): break
if(abs(r2-r1)<0.5): break
rate(30)
if(t>1.5):
v1+=a1*dt
r1+=v1*dt
ball1.pos=r1
r3+=v3*dt
plane.pos=r3
if(t>0.5):
v2+=a2*dt
r2+=v2*dt
else:
v2=v2
r2+=v2*dt
ball2.pos=r2
t+=dt
import matplotlib
import matplotlib.pyplot as plt
matplotlib.use("Agg")
import numpy as np
g=-9.8; v0=62.; H=40.
theta=np.radians(26.)
vx0=v0*np.cos(theta); vy0=v0*np.sin(theta)
r1=np.array([0.,0.]); v1=np.array([vx0,vy0])
a1=np.array([0., g])
r2=np.array([0.,H]); v2=np.array([20,0.])
a2=np.array([0., g])
r3=np.array([0.,H]); v3=np.array([20,0.])
a1=np.array([0., 0.])
t=0.; dt=0.01
t1=[];x1=[];y1=[];x2=[];y2=[];x3=[];y3=[]
while(t < 20.):
t1.append(t)
x1.append(r1[0]); y1.append(r1[1])
x2.append(r2[0]); y2.append(r2[1])
x3.append(r3[0]); y3.append(r3[1])
if( r1[1] < 0.): break
if( r2[1] < 0.): break
d=np.sqrt((r2[0]-r1[0])**2+(r2[1]-r1[1])**2)
if(d < 0.5):
print ('Hit the bomb:')
print ('%10.4f'*6 %(t,d,r1[0],r1[1],r2[0],r2[1]))
break
print ('%10.4f'*6 %(t,r1[0],r1[1],r2[0],r2[1],d))
if(t > 1.5):
v1+=a1*dt
r1+=v1*dt
r3+=v3*dt
if(t > 0.5):
v2+=a2*dt
r2+=v2*dt
else:
r2+=v2*dt
t+=dt
plt.plot(x1,y1,'r-')
plt.plot(x2,y2,'b--')
plt.plot(x3,y3,'k--')
plt.savefig("proj-vec-bomb.png")
plt.close()
練習
在給定的拋射角度和拋射速度之下,計算不同的阻力係數對最高高度以及最遠射程的函數關係。