numpy矩陣運算

      numpy是一個非常有用的數值計算工具，在這個講次中我們先簡單介紹舉證的定義方法和基本的操作。

    1. 陣列的轉置

      2.  我們利用x.T來取得x矩陣經轉置(行與列互換)後的矩陣。 
      import numpy as np
x = np.array([[1,2,3], [4,5,6], [7,8,9]])
print(x)
xT=x.T
print('after xT=x.T--print xT:--')
print(xT)
print('----x is not changed-----')
print (x)
print ('\n========consider 1D array===============')
print ('---transpose of 1d array has no effect----')
v = np.array([1,2,3])
print(v)
vT=v.T
print('after v.T----')
print(vT)
      ============輸出:============= 
      [[1 2 3]
 [4 5 6]
 [7 8 9]]
after xT=x.T--print xT:--
[[1 4 7]
 [2 5 8]
 [3 6 9]]
----x is not changed-----
[[1 2 3]
 [4 5 6]
 [7 8 9]]
========consider 1D array===============
---transpose of 1d array has no effect----
[1 2 3]
after v.T----
[1 2 3]

    2. 2維矩陣的每一列都加上一個一維陣列

      3.  在下面的程式中舉出三個三個版本的運算方式。
      1. 第1個方法直接用for loop進行每一列的加法這是最原始的方法
      2. 第2個方法使用了title的指令，它可以一次複製列成為一個矩陣，然後再進行矩陣的加法。
      3. 第3個方法在形式上最簡單，直接把矩陣跟向量相加(x+v)，因為在numpy的內定運算當中，當相加的兩個矩陣維度不一樣的時候會自動的把一維陣列的向量轉換成為一個相應的矩陣，然後再像第2個方法一樣將兩個矩陣相加。
      import numpy as np

#---method 1---
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
print('x=\n',x)
print('v=',v)
y = np.empty_like(x)   # Create an empty matrix with the same shape as x
for i in range(4):
    y[i, :] = x[i, :] + v
print('y=\n',y)

#---method 2---
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
vv = np.tile(v, (4, 1))   # Stack 4 copies of v on top of each other
print('\nvv=np.tile(v, (4,1))\nvv=',vv)
y = x + vv  # Add x and vv elementwise
print('y=\n',y)

#---method 3---
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = x + v  # Add v to each row of x using broadcasting
print('\n y=x+v=\n',y)
      ============輸出:============= 
      x=
 [[ 1  2  3]
 [ 4  5  6]
 [ 7  8  9]
 [10 11 12]]
v= [1 0 1]
y=
 [[ 2  2  4]
 [ 5  5  7]
 [ 8  8 10]
 [11 11 13]]
vv=np.tile(v, (4,1))
vv= [[1 0 1]
 [1 0 1]
 [1 0 1]
 [1 0 1]]
y=
 [[ 2  2  4]
 [ 5  5  7]
 [ 8  8 10]
 [11 11 13]]
 y=x+v=
 [[ 2  2  4]
 [ 5  5  7]
 [ 8  8 10]
 [11 11 13]]

    3. 矩陣相乘

      4.  給定兩個2x2的矩陣A,B

      \(A=
      \begin{bmatrix}
      1 & 2 \\
      3& 4
      \end{bmatrix},\space
      B=
      \begin{bmatrix}
      5 & 6 \\
      7 & 8
      \end{bmatrix}
      \)

      我們有兩種矩陣相乘的方法：

      • 矩陣乘法：


        • \(A\times B=
        \begin{bmatrix}
        \begin{bmatrix} 1 \times 5 + 2 \times 7 \end{bmatrix} & \begin{bmatrix} 1 \times 6 + 2 \times 8 \end{bmatrix} \\
        \begin{bmatrix} 3 \times 5 + 4 \times 7 \end{bmatrix} & \begin{bmatrix} 3 \times 6 + 4 \times 8 \end{bmatrix}
        \end{bmatrix}
        \)

        \(=
        \begin{bmatrix}
        \begin{bmatrix} 5 + 14 \end{bmatrix} & \begin{bmatrix} 6 + 16 \end{bmatrix} \\
        \begin{bmatrix} 15 + 28 \end{bmatrix} & \begin{bmatrix} 18 + 32 \end{bmatrix} \\
        \end{bmatrix}
        \)

        \(=
        \begin{bmatrix}
        19 & 22 \\
        43 & 50
        \end{bmatrix}
        \)

      • 矩陣相對應位置相乘：


        • \(=
        \begin{bmatrix}
        1\times 5 & 2\times 6 \\
        3\times 7 & 4\times 8
        \end{bmatrix}=
        \begin{bmatrix}
        5 & 12 \\
        21 & 32
        \end{bmatrix}
        \) 
      import numpy as np
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
print('A=\n',A)
print('B=\n',B)
print("\nA, B相乘(矩陣乘法) \n",A.dot(B))
print("\nA, B相對應位置相乘\n",A*B)
      ============輸出:============= 
      A=
 [[1 2]
 [3 4]]
B=
 [[5 6]
 [7 8]]
A, B相乘(矩陣乘法) 
 [[19 22]
 [43 50]]
A, B相對應位置相乘
 [[ 5 12]
 [21 32]]

    4. 陣列的乘法2

      5.
      • np.dot(a,b)
      • np.matmul(a,b)
      import numpy as np
import numpy as np
print('--dot array a with a scalar b')
print('--cannot use matmul for scalar---')
a=np.array([[1,2,3],[4,5,6],[7,8,9]])
b=3
c=np.dot(a,b)
print('a1=\n',a,a.shape)
print('b=',b)
print('np.dot(a,b)=\n',c,c.shape)
print('--array a3x3 with array b3x1--')
a=np.array([[1,2,3],[4,5,6],[7,8,9]])
b=np.array([2,4,6])
c=np.dot(a,b)
print('a=\n',a,a.shape)
print('b=',b,b.shape)
print('c=',c,c.shape)
print('np.matmul(a,b)=',np.matmul(a,b))
print('--array a3x3 with array b3x2--')
a=np.array([[1,2,3],[4,5,6],[7,8,9]])
b=np.array([[1,2],[3,4],[5,6]])
c=np.dot(a,b)
print(a,a.shape)
print(b,b.shape)
print(c,c.shape)
print('np.matmul(a,b)=\n',np.matmul(a,b))
      		============輸出:============= 
      --dot array a with a scalar b
--cannot use matmul for scalar---
a1=
 [[1 2 3]
 [4 5 6]
 [7 8 9]] (3, 3)
b= 3
np.dot(a,b)=
 [[ 3  6  9]
 [12 15 18]
 [21 24 27]] (3, 3)
--array a3x3 with array b3x1--
a=
 [[1 2 3]
 [4 5 6]
 [7 8 9]] (3, 3)
b= [2 4 6] (3,)
c= [ 28  64 100] (3,)
np.matmul(a,b)= [ 28  64 100]
--array a3x3 with array b3x2--
[[1 2 3]
 [4 5 6]
 [7 8 9]] (3, 3)
[[1 2]
 [3 4]
 [5 6]] (3, 2)
[[ 22  28]
 [ 49  64]
 [ 76 100]] (3, 2)
np.matmul(a,b)=
 [[ 22  28]
 [ 49  64]
 [ 76 100]]

    5. 陣列的轉置

      6.  我們利用x.T來取得x矩陣經轉置(行與列互換)後的矩陣。
      ============輸出:=============

    6. 陣列的轉置

      7.  我們利用x.T來取得x矩陣經轉置(行與列互換)後的矩陣。
      ============輸出:=============

    7. 陣列的轉置

      8.  我們利用x.T來取得x矩陣經轉置(行與列互換)後的矩陣。
      ============輸出:=============

    8. 陣列的轉置

      9.  我們利用x.T來取得x矩陣經轉置(行與列互換)後的矩陣。
      ============輸出:=============

    9. numpy的應用5+matplot 3D

      10.  
      import matplotlib
import matplotlib.pyplot as plt
matplotlib.use("Agg")
import numpy as np

x1 = np.linspace(-2,2,5)
print ('x1=',x1)
x2=np.mgrid[-2:2:5j]
print ('x2=',x2)

x,y=np.mgrid[-2:2:5j,-2:2:5j]
print ('x=',x)
print ('y=',y)

x,y=np.mgrid[-2:2:10j,-2:2:10j]
plt.axis("equal")
plt.plot(x,y,'bo')
plt.savefig("5x5.png")

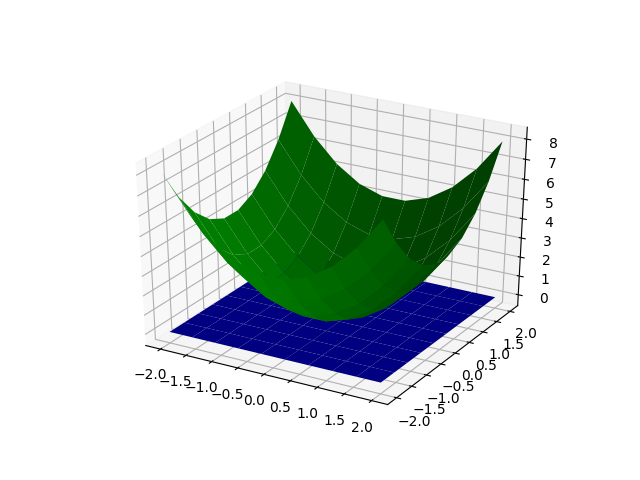
z=x**2+y**2
z2=x*0+y*0
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.plot_surface(x, y, z, color="g")
ax.plot_surface(x, y, z2, color="b")
ax.scatter(0,0,0, color="k")
plt.savefig("mgrid-3D-1.png")
print ('plot is done')