高斯定律
高斯定律(Gauss' law)表明在閉合曲面內的電荷分佈與產生的電場之間的關係: 其定性描述為:穿越出任意閉合曲面的淨電通量\(\Phi_E\)等於該閉合曲面內的淨電荷(\(Q\))除以電容率(\(\epsilon_0\)): \[\Phi_E=\dfrac{Q_{\text{enc}}}{\epsilon_0}.\] 該閉合曲面稱為高斯曲面,\(Q_{enc}\)是封閉曲面(高斯面)內的電荷總量。考慮電通量的定義我們可以將高斯定律寫成下面的數學形式: \[\Phi_E=\oint_S \vec{E} \cdot \mathrm{d}\mathbf{S} = \dfrac{Q_{\text{enc}}}{\epsilon_0}.\] \(\oint_S\)代表隊封閉的曲面(\(S\))的面積分。
如果電場為一非均勻電場,則通常會將此一較大面積的電通量分割,改取一小塊面積 \( d\mathbf{S}\) 上的電通量 \(d\Phi_{E}\) \[ d\Phi_{E}=\mathbf{E} \cdot \mathrm{d}\mathbf{S}\] (電場 \(\mathbf {E}\)乘以垂直於所選面積表面的分量)。因此,表面 \(S\) 上的電通量可由表面積分得到:
\(\Phi_{E}=\oint_{S} \mathrm{d}\Phi= \oint_{S} \mathbf{E} \cdot \mathrm{d} \mathbf{S}\)
其中 \(\mathbf{E}\)是電場,\(\mathrm{d} \mathbf{S}\)是閉合表面\(S\)上的微小面積,其方向定義為表面法線朝外。
根據高斯定律,通過任一封閉曲面(高斯面)的淨電通量(\(\Phi_{E}\)),必與該封閉曲面內所圍之淨電荷量(\( Q_{\rm{enc}}\))成正比。 而在真空中,此比例常數為一定值\( 1/\varepsilon_{0}\)。其數學式為 :
\(\Phi_{E}=\oint_{\scriptstyle{S}} \mathbf{E} \cdot d\mathbf{S} =\frac{Q_{\rm{enc}}}{\varepsilon_{0}} \)
其中 \(\mathbf{E}\)是電場、 \(S\) 是任一封閉曲面、 \( Q_{\rm {enc}}\) 是曲面 \(S\) 內的總淨電荷。\(\varepsilon_{0}\)是介電常數(為一通用常數,也稱為真空中電容率或真空介電常數 )。\( \varepsilon _{0}\approx 8.85...\times 10^{-12}\) (F/m) 此一關係式以其積分形式被稱為電場高斯定律,是四個馬克士威方程式之一。電通量的單位為伏特米(V·m)。
此方程式是高斯在1835年提出的,但直到1867年才發布。因為數學上的相似性,高斯定律也可以應用於其它由反平方定律決定的物理量,例如重力或者輻照度。 在我們開始進行高斯定律的應用之前,我們很快地將電通量的內容再複習一遍。 我們著重在兩個情況:一個是平面的電通量,另外一個是球面的電通量。當然我們也可以考慮圓柱面的電通量。
計算點電荷對一平面的電通量
|
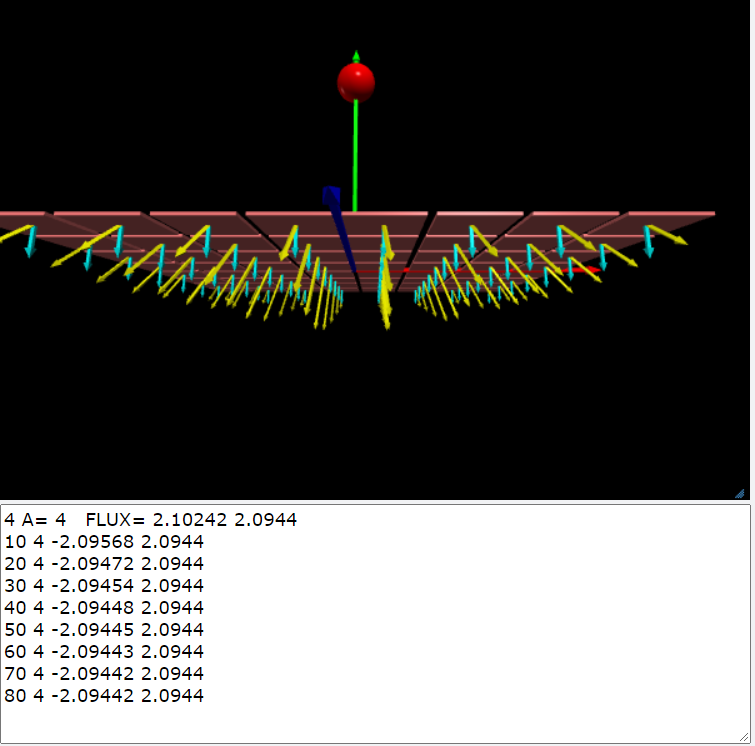
\(-R \le x \le R; \\ -R \le z \le R \\ L=2R; R=1 \\ A=L^2=4; \,k=1\) 點電荷\(q=1, \vec{r}_q=(0,L/2,0)\)的電場: \(\vec{E}=k q_1 / |\vec{r}-\vec{r_q}|^3 (\vec{r}-\vec{r_q})\) xz-平面的法線: \(\hat{n}=(0,1,0)\) 電通量\(\Phi_E\): \(\Phi_E=\int_S \vec{E} \cdot \mathrm{d}\vec{S} \\ =\int_{-R}^{R} \int_{-R}^{R} \vec{E} \cdot \hat{n} \,dx dz \\ =\dfrac{4 \pi}{6}\simeq 2.0944\) |
|
一個點電荷對兩個平面的電通量
|
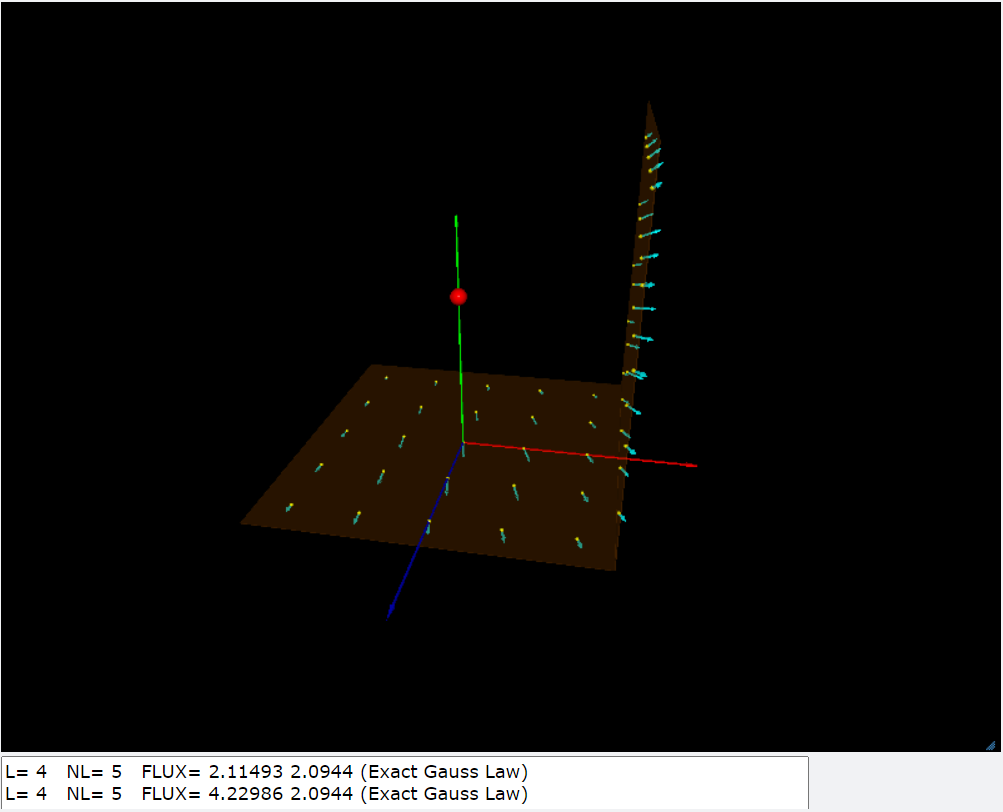
電通量\(\Phi_E\): \(\Phi_E=\int_{S_1} \vec{E} \cdot \mathrm{d}\vec{S} + \int_{S_2} \vec{E} \cdot \mathrm{d}\vec{S} \\ =2 \times \int_{-R}^{R} \int_{-R}^{R} \vec{E} \cdot \hat{n} \,dx dz \\ =2 \times \dfrac{4 \pi}{6}\simeq 4.18\) 因此我們可以利用對稱性考慮,如果有一個邊長\(L=2R\)的立方體,當中有一個點電荷(\(q=1\))放置在立方體的中心位置,那麼立方體的六個面的電通量之總和必然為\(\Phi_E=6 \times \dfrac{4\pi k_e q}{6}=4 \pi k_e q=\dfrac{q}{\varepsilon_0}\),這就是高斯定律的結果。 |
|
glowscript:一個點電荷對兩個平面的電通量(PS-EFlux-06.py)
球座標
|
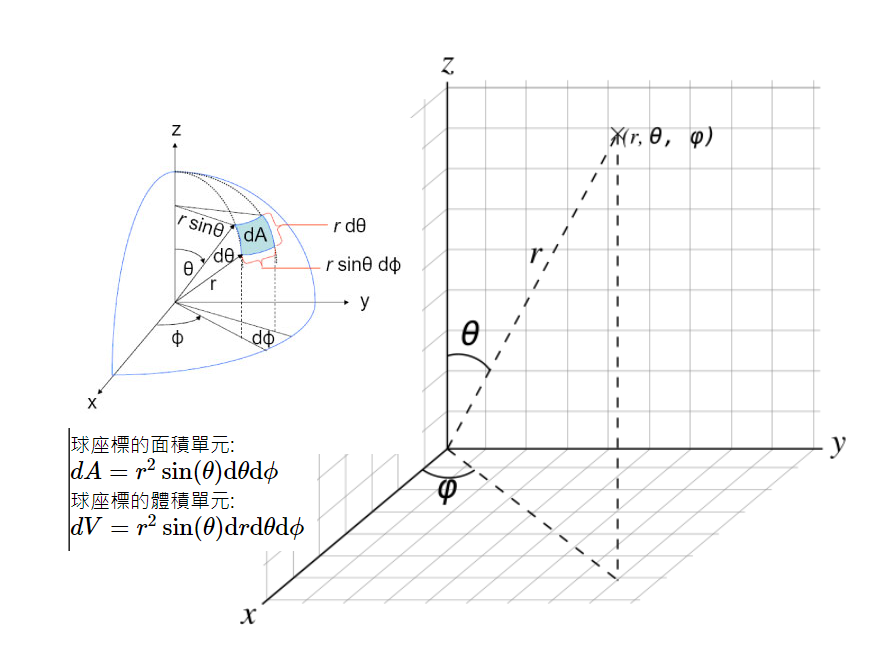
球座標\(\rightarrow\)直角坐標系的轉換公式: \(x=r \cos \phi \sin \theta; \\ y=r \cos \theta \\ z=r \cos \theta;\) 直角坐標系\(\rightarrow\)球座標的轉換公式: \(r=\sqrt{x^2+y^2+z^2} \\ \theta=\cos^{-1} \dfrac{\sqrt{x^2+y^2}}{\sqrt{x^2+y^2+z^2}} \\ \phi=\tan^{-1} \dfrac{y}{x} \) 球座標的面積單元: \(dA=r^2 \sin(\theta) \mathrm{d}\theta \mathrm{d}\phi \) 球座標的體積單元: \(dV=r^2 \sin(\theta) \mathrm{d}r \mathrm{d}\theta \mathrm{d}\phi \) |
|
球面的面積與球的體積
|
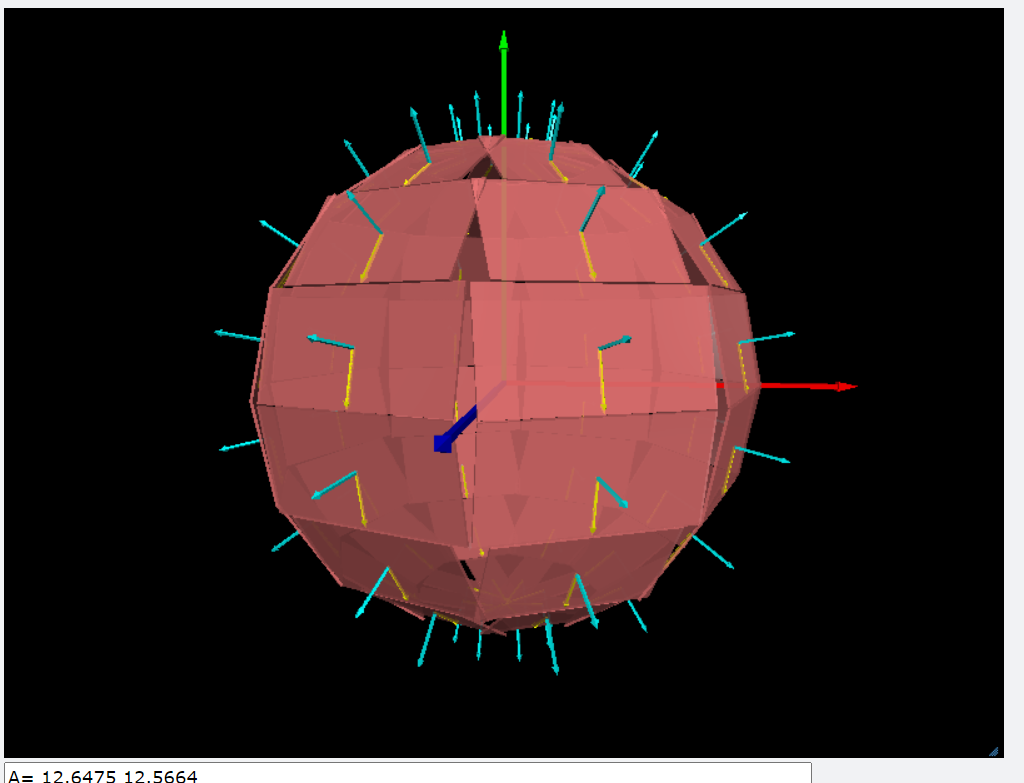
對一個半徑為R的球,球面面積: \(A=\int_0^{\pi} \mathrm{d}\theta \int_0^{2\pi} \mathrm{d}\phi \, R^2 \sin \theta \\ =\int_0^{\pi} \sin \theta \mathrm{d}\theta \int_0^{2\pi} R^2 \mathrm{d}\phi= (2)(2\pi R^2) \\ =4\pi R^2\) 球的體積: \(V=\int_0^R \mathrm{d}r \int_0^{\pi} \mathrm{d}\theta \int_0^{2\pi} \mathrm{d}\phi \, r^2 \sin \theta \\ = \int_0^R r^2 \mathrm{d}r \int_0^{\pi} \sin \theta \mathrm{d}\theta \int_0^{2\pi} R^2 \mathrm{d}\phi \\ = (\dfrac{1}{3} R^3 )(2)(2\pi) \\ =\dfrac{4}{3}\pi R^3\) |
|
glowscript:球面的面積與球的體積(PS-EFlux-08.py)
一個點電荷對半球面的電通量
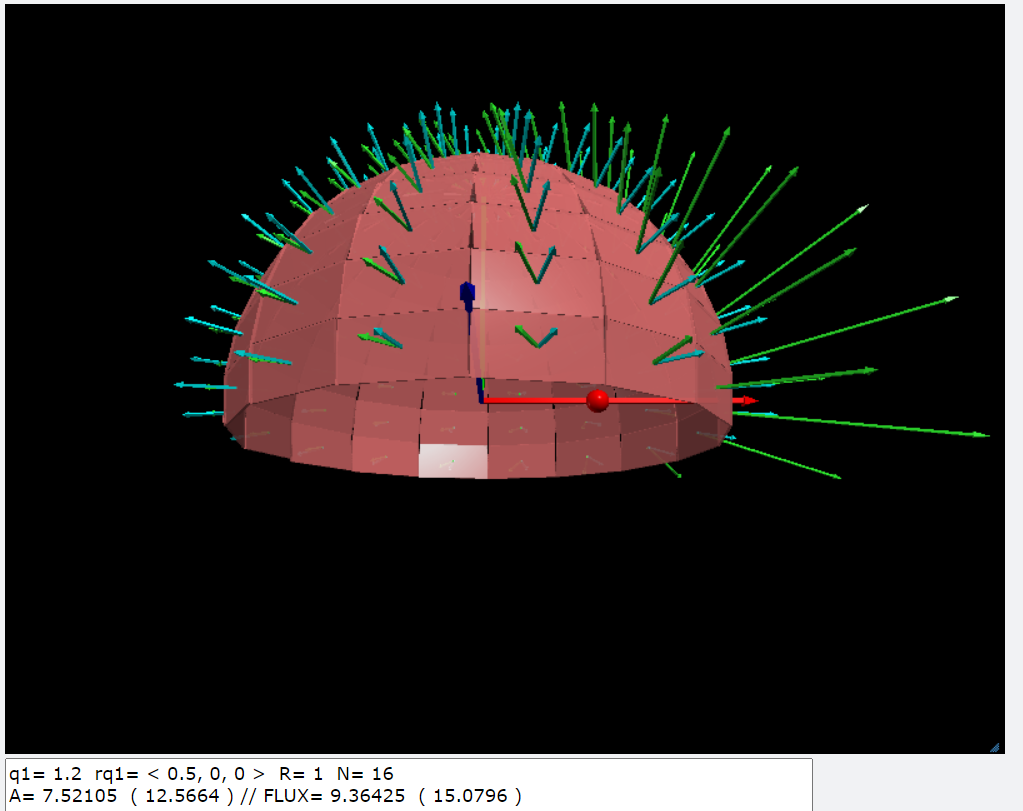
| 在這個計算當中我們選取的曲面是一個半徑為R的球面,座標的原點就設在球心上。因為我們把原點設在球的球心,因此每一個球面上的點的法向量就是位置向量。我們只要利用函數副程式(EF_points)計算出這個點的電場: 點電荷q的座標\(\vec{r'}\), 欲計算的電場位置\(\vec{r}\), 電場(\(\vec{E}\))在置\(\vec{r}\)的向量: \[ \vec{E}(\vec{r})=\frac{kq}{r^3}\vec{r} \] 再將\(\vec{E}\)與位置向量\(\vec{r}\)取內積,很快可以把面積分算出來。三維空間裏,還有其他的座標系,例如圓柱座標係就是其中一種當。我們考慮我們的電荷呈線性分佈時,圓柱座標係就是一個比較好的選擇,因為這個時候的高斯面應該會是圓柱體的表面比較能夠符合電場問題的對稱性。程式中 dA=R*dt*R*sin(T)*df就是球座標系的面積微量元素:\(dA=R^2 \sin(\theta) d \theta d \phi\)。 |
|
glowscript:一個點電荷對半球面的電通量(PS-EFlux-09.py)
封閉的曲面--高斯面--高斯定律
一個點電荷對立方體面的電通量
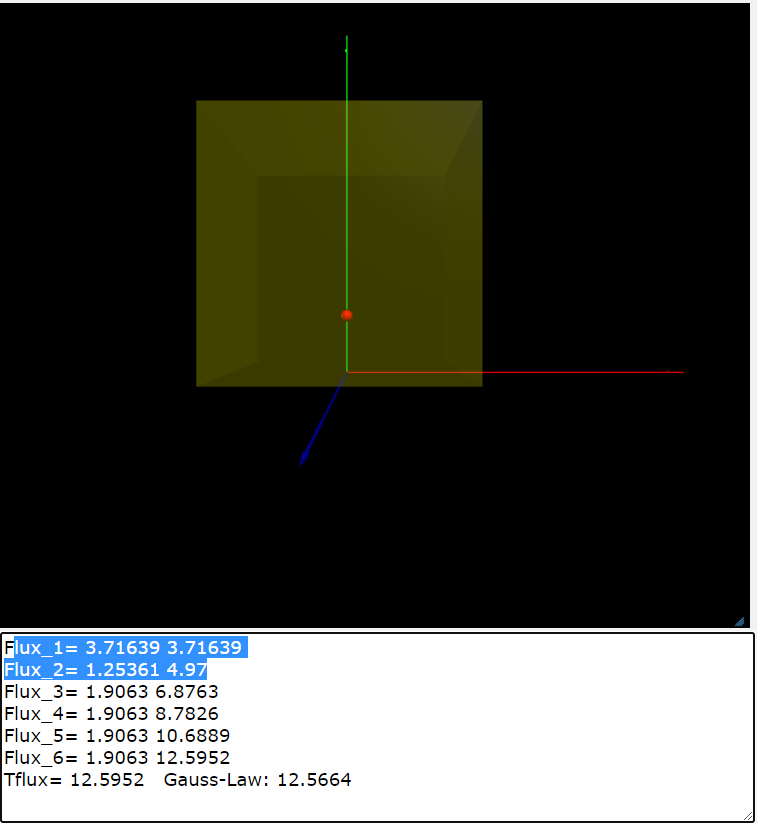
| 在前面的討論中我們已經得到1個點電荷如果放在立方體的正中央,電場對6個面的電通量的總和會等於電荷的電量除以\(\varepsilon_0\),這就是高斯定律。在下面的程式當中我們將電荷的位置移開體心,向下方偏移。利用vpython程式我們可以計算在這個情況下,通過封閉曲面的電通量總和。數值計算的結果顯示總和不變,仍然是高斯定律說給出的結果\(\Phi_E=\dfrac{Q_{\mathrm{enc}}}{\varepsilon_0}\)。我們知道如果電荷向下偏移,將會因為電荷較為靠近底面,通過底面的電場強度增加,底面的電通量將會增加;相對的頂面的電通量將會減少,在這增長與消長之間,電通量的總和維持不變,就是高斯定律的精神。 |
|
GlowScript 3.2 VPython
def EF_point(q,rq,r):
ke=1.; rrq=r-rq
E=ke*q*rrq/mag(rrq)**3
return E
L=4; NL=10; dx=L/NL; dz=L/NL; da=dx*dz
q1=1.; rq1=vec(0,L/4,0.)
scene=canvas(width=600, height=500, center=vec(0.5,L/4,0))
X=arrow(pos=vec(0,0,0),axis=vec(6,0,0),shaftwidth=0.02,headwidth=0.04,color=vec(1,0,0))
Y=arrow(pos=vec(0,0,0),axis=vec(0,6,0),shaftwidth=0.02,headwidth=0.04,color=vec(0,1,0))
Z=arrow(pos=vec(0,0,0),axis=vec(0,0,6),shaftwidth=0.02,headwidth=0.04,color=vec(0,0,1))
Q1=sphere(pos=rq1,radius=0.1,color=vec(1,0,0))
Gauss=box(pos=vec(0,L/2,0),size=vec(L,L,L),color=vec(1,1,0),opacity=0.2)
dx=L/NL; dz=L/NL; dy=L/NL; da=dx*dz;
Tflux=0
eflux=0; n=vec(0,-1,0)
for i in range(NL):
x=-L/2+dx*(i+0.5)
for j in range(NL):
z=-L/2+dz*(j+0.5)
r=vec(x,0,z)
E=EF_point(q1,rq1,r)
Eda=dot(E,n)*da
eflux+=Eda
Tflux+=eflux
print('Flux_1=',eflux,Tflux)
eflux=0; n=vec(0,1,0)
for i in range(NL):
x=-L/2+dx*(i+0.5)
for j in range(NL):
z=-L/2+dz*(j+0.5)
r=vec(x,L,z)
E=EF_point(q1,rq1,r)
Eda=dot(E,n)*da
eflux+=Eda
Tflux+=eflux
print('Flux_2=',eflux,Tflux)
eflux=0; n=vec(1,0,0)
for i in range(NL):
y=0+dy*(i+0.5)
for j in range(NL):
z=-L/2+dz*(j+0.5)
r=vec(L/2,y,z)
E=EF_point(q1,rq1,r)
Eda=dot(E,n)*da
eflux+=Eda
Tflux+=eflux
print('Flux_3=',eflux,Tflux)
eflux=0; n=vec(-1,0,0)
for i in range(NL):
y=0+dy*(i+0.5)
for j in range(NL):
z=-L/2+dz*(j+0.5)
r=vec(-L/2,y,z)
E=EF_point(q1,rq1,r)
Eda=dot(E,n)*da
eflux+=Eda
Tflux+=eflux
print('Flux_4=',eflux,Tflux)
eflux=0; n=vec(0,0,1)
for i in range(NL):
x=-L/2+dx*(i+0.5)
for j in range(NL):
y=0+dy*(j+0.5)
r=vec(x,y,L/2)
E=EF_point(q1,rq1,r)
Eda=dot(E,n)*da
eflux+=Eda
Tflux+=eflux
print('Flux_5=',eflux,Tflux)
eflux=0; n=vec(0,0,-1)
for i in range(NL):
x=-L/2+dx*(i+0.5)
for j in range(NL):
y=0+dy*(j+0.5)
r=vec(x,y,-L/2)
E=EF_point(q1,rq1,r)
Eda=dot(E,n)*da
eflux+=Eda
Tflux+=eflux
print('Flux_6=',eflux,Tflux)
print('Tflux=',Tflux,' Gauss-Law:',4*pi*q1)
glowscript:一個點電荷對立方體面的電通量(PS-Gauss-01.py)
q1= 1.5 rq1= < 1.3, 0.3, 0.3 > R= 1 N= 8 A= 12.6475 ( 12.5664 ) // FLUX= -0.266703 N= 16 A= 12.5866 ( 12.5664 ) // FLUX= -0.0726721 N= 32 A= 12.5714 ( 12.5664 ) // FLUX= 1.84141e-3 N= 64 A= 12.5676 ( 12.5664 ) // FLUX= 3.84025e-4 N= 128 A= 12.5667 ( 12.5664 ) // FLUX= 9.59969e-5
一個點電荷對立方體面的電通量,電荷在外
|
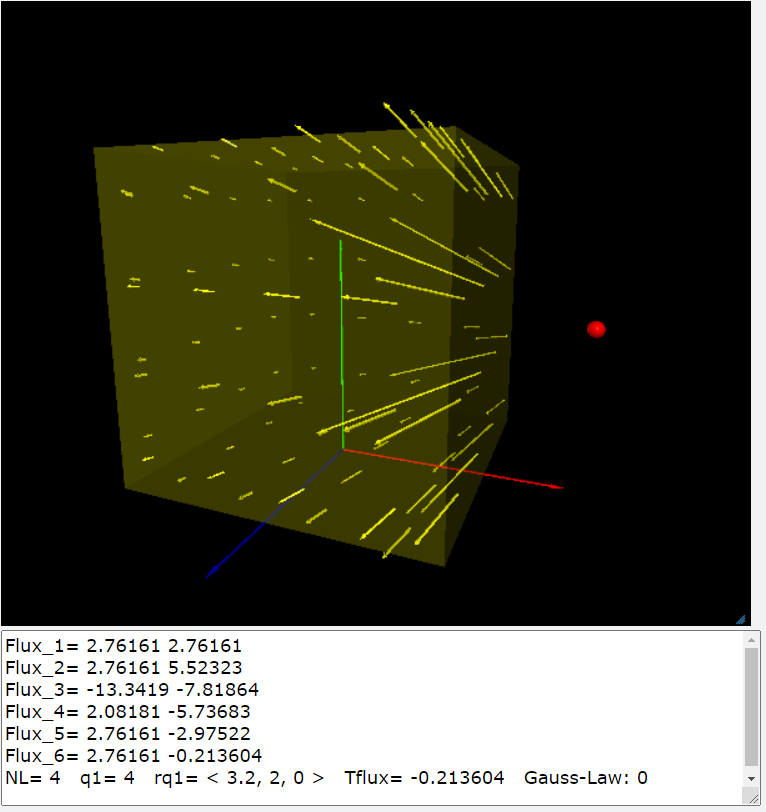
若是點電荷在立方體的外側,\(Q_{\mathrm{enc}}=0\),根據高斯定律,高斯面的電通量\(\Phi_E=0\)。 glowscript:一個點電荷對立方體面的電通量,電荷在外(PS-Gauss-01B.py) 隨著我們切割表面的積分單元越細緻(N越大), 積分的結果就越接近於高斯定律:\(Q_{\mathrm{enc}}=0\) NL= 4 q1= 4 rq1= < 3.2, 2, 0 > -0.213604 NL= 8 q1= 4 rq1= < 3.2, 2, 0 > -0.0660521 NL= 16 q1= 4 rq1= < 3.2, 2, 0 > -0.0165127 NL= 32 q1= 4 rq1= < 3.2, 2, 0 > -4.12771e-3 |
|
一個點電荷對高斯球面的電通量
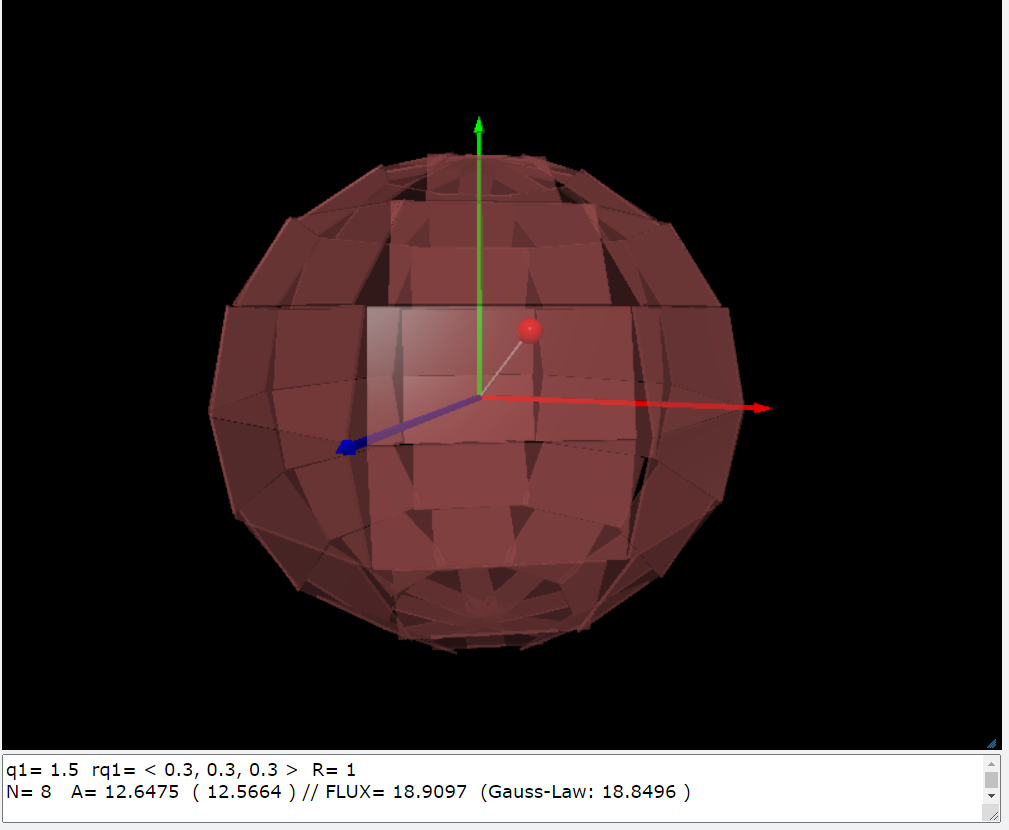
| 在這個計算當中我們選取的曲面是一個半徑為R的球面,座標的原點就設在球心上。因為我們把原點設在球的球心,因此每一個球面上的點的法向量就是位置向量。我們只要利用函數副程式(EF_points)計算出這個點的電場: 點電荷q的座標\(\vec{r'}\), 欲計算的電場位置\(\vec{r}\), 電場(\(\vec{E}\))在置\(\vec{r}\)的向量: \[ \vec{E}(\vec{r})=\frac{kq}{r^3}\vec{r} \] 再將\(\vec{E}\)與位置向量\(\vec{r}\)取內積,很快可以把面積分算出來。三維空間裏,還有其他的座標系,例如圓柱座標係就是其中一種當。我們考慮我們的電荷呈線性分佈時,圓柱座標係就是一個比較好的選擇,因為這個時候的高斯面應該會是圓柱體的表面比較能夠符合電場問題的對稱性。程式中 dA=R*dt*R*sin(T)*df就是球座標系的面積微量元素:\(dA=R^2 \sin(\theta) d \theta d \phi\)。 |
|
GlowScript 3.2 VPython
scene=canvas(width=800, height=600, center=vector(0.1,0.1,0), forward=vec(-0.3,-0.1,-1))
X=arrow(pos=vec(0,0,0),axis=vec(1.2,0,0),shaftwidth=0.02,headwidth=0.04,color=vec(1,0,0))
Y=arrow(pos=vec(0,0,0),axis=vec(0,1.2,0),shaftwidth=0.02,headwidth=0.04,color=vec(0,1,0))
Z=arrow(pos=vec(0,0,0),axis=vec(0,0,1.2),shaftwidth=0.02,headwidth=0.04,color=vec(0,0,1))
R=1; N=8; dt=pi/N; df=2*pi/N
q1=1.5; rq1=vec(0.3,0.3,0.3); ke=1
Q1=sphere(pos=rq1,radius=0.05,color=vec(1,0,0))
arrow(pos=vec(0,0,0),axis=rq1,shaftwidth=0.01,headwidth=0.02,color=vec(1,1,1))
A=0; FLUX=0
for i in range(N):
t=dt*(i+0.5)
for j in range(N):
f=df*(j+0.5)
x=R*sin(t)*cos(f); z=R*sin(t)*sin(f); y=R*cos(t)
r=vec(x,y,z)
n=hat(r)
r1=vec(R*sin(t+0.01)*cos(f),R*cos(t+0.01),R*sin(t+0.01)*sin(f))
tv=hat(r1-r)
b=box(pos=r,size=vec(R*dt,0.01,R*sin(t)*df),axis=tv,up=r,color=vec(1,0.5,0.5),opacity=0.3)
E=ke*q1/mag2(r-rq1)*hat(r-rq1)
#arrow(pos=r,axis=b.up*0.2,shaftwidth=0.01,headwidth=0.02,color=vec(0,1,1))
#arrow(pos=r,axis=E*0.2,shaftwidth=0.01,headwidth=0.02,color=vec(0.2,1,0.2))
A+=R**2*sin(t)*dt*df
FLUX+=dot(E,n)*R**2*sin(t)*dt*df
print('q1=',q1,' rq1=',rq1,' R=',R)
print('N=',N,' A=',A,' (',4*pi*R**2,') // FLUX=',FLUX,' (Gauss-Law:',4*pi*q1,')')
glowscript:一個點電荷對高斯球面的電通量(PS-Gauss-02.py)
隨著我們切割球面的積分單元越細緻(N越大),積分的結果就越接近於高斯定律的數值18.8496。 q1= 1.5 rq1= < 0.3, 0.3, 0.3 > R= 1 N= 8 A= 12.6475 ( 12.5664 ) // FLUX= 18.9097 (Gauss-Law: 18.8496 ) N= 16 A= 12.5866 ( 12.5664 ) // FLUX= 18.8764 (Gauss-Law: 18.8496 ) N= 32 A= 12.5714 ( 12.5664 ) // FLUX= 18.8563 (Gauss-Law: 18.8496 ) N= 64 A= 12.5676 ( 12.5664 ) // FLUX= 18.8512 (Gauss-Law: 18.8496 ) N= 128 A= 12.5667 ( 12.5664 ) // FLUX= 18.85 (Gauss-Law: 18.8496 )
PS-Gauss-Cobe-q-out.png
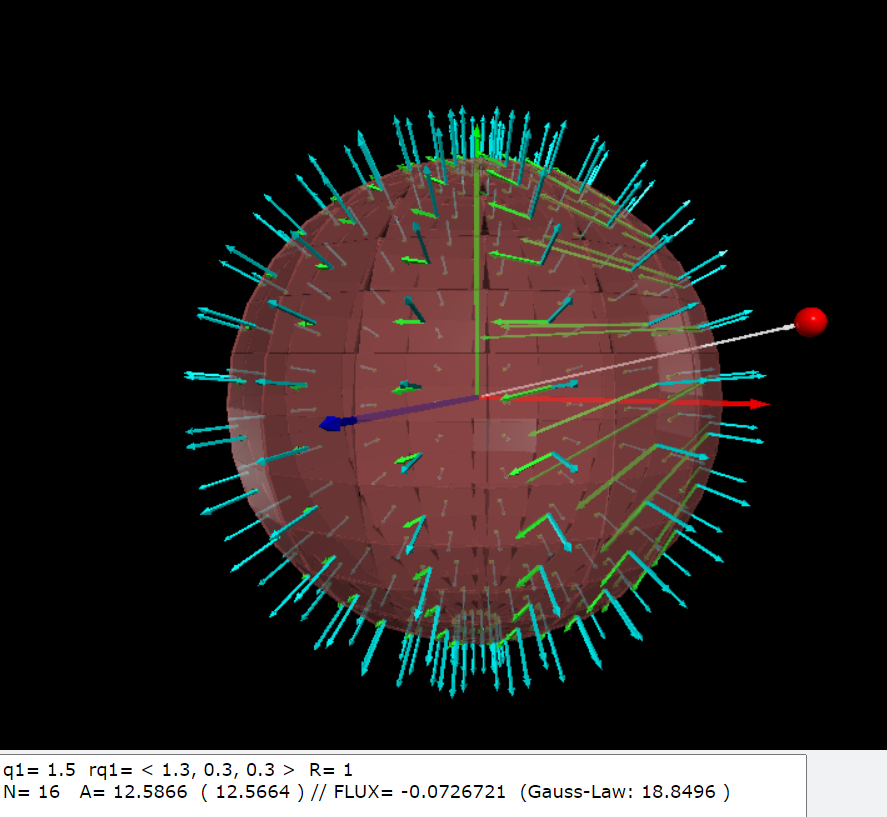
點電荷在高斯球面之外
| 如果點電荷在高斯球面之外,那麼接近點電荷這一面的法線與電場的方向大約是反方向的,因此這一部分的電通量貢獻是負的;相對的遠離點電荷的另外的球面的法線與電場同方向大致同方向,因此電通量的貢獻是正的。根據高斯定律,高斯面的電通量是高斯面內的淨電荷,在這個情況下淨電荷為零,因此高斯面的電通量應該是0。我們可以執行上面這個程式,把電荷放到高斯面的外面,rq1=vec(1.3,0.3,0.3),並且觀察不同的切割數目(N)所得的結果,不難發現電通量確實為零,也就驗證了高斯定律的正確性。 |
|
q1= 1.5 rq1= < 1.3, 0.3, 0.3 > R= 1 N= 8 A= 12.6475 ( 12.5664 ) // FLUX= -0.266703 N= 16 A= 12.5866 ( 12.5664 ) // FLUX= -0.0726721 N= 32 A= 12.5714 ( 12.5664 ) // FLUX= 1.84141e-3 N= 64 A= 12.5676 ( 12.5664 ) // FLUX= 3.84025e-4 N= 128 A= 12.5667 ( 12.5664 ) // FLUX= 9.59969e-5