磁場、磁力線與磁力

電流是磁場的來源--Biot-Savart定律
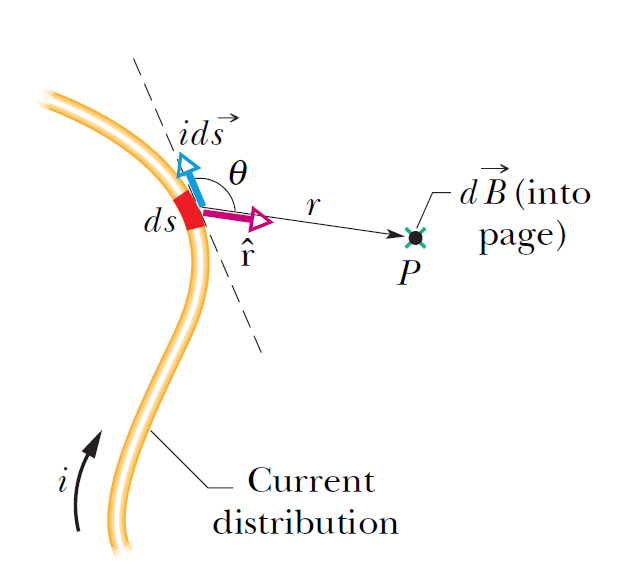 圖中顯示了一個攜帶電流i的任意形狀的導線。我們想要找到在附近的一點P的磁場。我們首先在將導線分割成電流元素ds,然後為每個元素定義一個長度向量\(d\vec{s}\)其長度ds,其方向是ds電流的方向。然後定義一個差分電流長度元素為\(id\vec{s}\);我們希望計算由一個典型的電流長度元素在P點產生的場\(d\vec{B}\)。從實驗中我們發現像電場這樣的磁場可以被疊加來找到一個總和的磁場。因此,我們可以通過求和(數值求和),通過積分來計算,所有電流長度元素在P點所貢獻的淨磁場\(\vec{B}\)。但是,這個總和比電場相關的過程更具挑戰性和複雜性。產生電場的電荷元素dq是純量,產生磁場的電流長度元素為\(id\vec{s}\)是向量。
圖中顯示了一個攜帶電流i的任意形狀的導線。我們想要找到在附近的一點P的磁場。我們首先在將導線分割成電流元素ds,然後為每個元素定義一個長度向量\(d\vec{s}\)其長度ds,其方向是ds電流的方向。然後定義一個差分電流長度元素為\(id\vec{s}\);我們希望計算由一個典型的電流長度元素在P點產生的場\(d\vec{B}\)。從實驗中我們發現像電場這樣的磁場可以被疊加來找到一個總和的磁場。因此,我們可以通過求和(數值求和),通過積分來計算,所有電流長度元素在P點所貢獻的淨磁場\(\vec{B}\)。但是,這個總和比電場相關的過程更具挑戰性和複雜性。產生電場的電荷元素dq是純量,產生磁場的電流長度元素為\(id\vec{s}\)是向量。距離r處的點P產生的場的大小由電流長度\(id\vec{s}\)決定: \[dB=\frac{\mu_0}{4\pi}\frac{ids\sin \theta}{r^2}\] \(\theta\)是\(\hat{r}\) 和\(id\vec{s}\)之間的角度,\(\hat{r}\)是由ds指向P的單位向量。符號\(\mu_0\)是一個常數,稱為真空磁導率常數,其值為\[\mu_0=4\pi \times 10^{-7} \simeq 1.26 \times 10^{-6} \] 如圖顯示\(d\vec{B}\)的方向是指向頁面的方向,即為外積\(d\vec{s} \times \hat{r}\)的方向。因此,我們可以寫向量形式為 \[d\vec{B}=\frac{\mu_0}{4\pi}\frac{id\vec{s} \times \hat{r}}{r^2}\] 此稱為Biot-Savart定律。這是實驗上推導出來的,是一個反平方定律。我們將用這個法則來計算通過各種電流分佈在某一點產生的淨磁場\(\vec{B}\).
長直電流導線所生之磁場
|
電流線沿著z-axis擺設,電流的流向+z。磁力線形成同心圓狀並且與電流導線垂直。 |
 |
GlowScript 3.2 VPython
scene = canvas(width=800, height=600, center=vec(0, 0, 0.5),
background=vec(0,0,0), forward=vec(-1,-1,-1))
| |
|
glowscript:長直電流導線所生之磁場(PS-BFL-current-line.py) | |
單一電流環所生的磁場
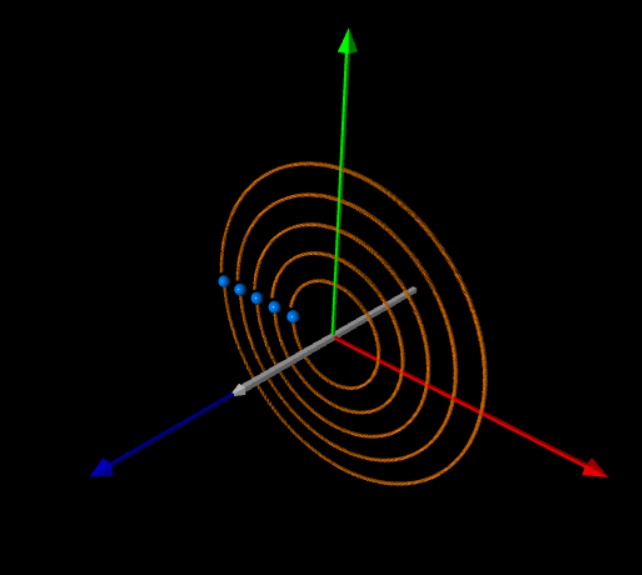
| 在下面的程式當中,產生磁場的電流源取代為一個電流環,磁場的貢獻由一段一段的電流元素,在空間中的向量求和而得到。凈磁場的磁力線分佈如圖形所顯現的,從內部向外彎曲形成一個迴路。 |
 |
GlowScript 3.2 VPython
scene=canvas(width=800,height=800,center=vec(0,0,0),background=vec(0,0,0),forward=vec(-1,-1,-1))
def BF_coil_1(R,Ni,ic,r,br,bc):
mu0=1.
ds=2.*pi*R/Ni
B=vec(0.,0.,0.)
for i in range(Ni):
t=2.*pi/Ni*i
rp=vec(R*cos(t),R*sin(t),0)
dl=ds*vec(-sin(t),cos(t),0.)
rrp=r-rp
dB=mu0*ic/4.*pi*cross(dl,rrp)/mag(rrp)**3
B=B+dB
return B
def Bline(R,Ni,ic,r,br,bc,a):
maxi=2000
ss=0.01
ri=r
for i in range(maxi):
B=BF_coil_1(R,Ni,ic,r,br,bc)
curr=1
nr=r+B/mag(B)*ss
arr=arrow(pos=r,axis=nr-r,shaftwidth=0.02,headwidth=0.02,color=a)
r=nr
dr=mag(r-ri)
if(i>100 and dr < 0.08): break
if(i>100 and dr > 3.5): break
return
ic=5; R=1.; Ni=40; br=0.1
arrx=arrow(pos=vec(0,0,0),axis=vec(4,0,0),shaftwidth=0.02,headwidth=0.02,color=vec(1,0,0))
arrY=arrow(pos=vec(0,0,0),axis=vec(0,4,0),shaftwidth=0.02,headwidth=0.02,color=vec(0,1,0))
arrZ=arrow(pos=vec(0,0,0),axis=vec(0,0,4),shaftwidth=0.04,headwidth=0.02,color=vec(0,0,1))
ring(pos=vec(0,0,0),radius=R,axis=vec(0,0,1),color=vec(1,1,1),thickness=0.02)
[sphere(pos=vec(-0.7+0.2*i,0.0,0),color=vec(0,0.5,1),radius=0.05) for i in range(8)]
arrow(pos=vec(0,R,0),axis=vec(-0.3,0,0),shaftwidth=0.04,color=vec(1,1,0))
bc=vec(1,0.5,0)
for i in range(8):
scene.pause('click')
xi=-0.7+0.2*i
r=vec(xi,0.0,0)
Bline(R,Ni,ic,r,br,bc,bc)
|
|
|
glowscript:單一電流環所生的磁場(PS-BFL-current-loop.py) | |
二電流環所建立的磁場(磁瓶子)
| 我們把前一個程式再繼續的延伸,考慮兩個電流環所產生的磁場。我們把兩個電流環分佈在一個距離上,那麼這樣子所產生的磁場會在兩個環之間形成一個像瓶子一樣的磁場分佈,這樣的磁場分佈稱為磁瓶子(magnetic bottle)。 |
 |
GlowScript 3.2 VPython
scene=canvas(width=800,height=800,center=vec(0,0,2),background=vec(0,0,0),forward=vec(-1,-1,-1))
def BF_coil_2(R,Z2,Ni,ic,r,br,bc):
mu0=1.
ds=2.*pi*R/Ni
B=vec(0.,0.,0.)
for i in range(Ni):
t=2.*pi/Ni*i
rp=vec(R*cos(t),R*sin(t),0)
dl=ds*vec(-sin(t),cos(t),0.)
rrp=r-rp
dB=mu0*ic/4.*pi*cross(dl,rrp)/mag(rrp)**3
B=B+dB
for i in range(Ni):
t=2.*pi/Ni*i
rp=vec(R*cos(t),R*sin(t),Z2)
dl=ds*vec(-sin(t),cos(t),0.)
rrp=r-rp
rrp0=mag(rrp)
dB=mu0*ic/4.*pi*cross(dl,rrp)/rrp0**3
B=B+dB
return B
def Bline(R,Z2,Ni,ic,r,br,bc,a):
maxi=2000
ss=0.01
ri=r
for i in range(maxi):
B=BF_coil_2(R,Z2,Ni,ic,r,br,bc)
curr=1
nr=r+B/mag(B)*ss
arr=arrow(pos=r,axis=nr-r,shaftwidth=0.02,headwidth=0.02,color=a)
r=nr
dr=mag(r-ri)
if(i>100 and dr < 0.08): break
if(i>100 and dr > 3.5): break
return
ic=5; R=1.; Z2=4; Ni=40; br=0.1
arrx=arrow(pos=vec(0,0,0),axis=vec(4,0,0),shaftwidth=0.02,headwidth=0.02,color=vec(1,0,0))
arrY=arrow(pos=vec(0,0,0),axis=vec(0,4,0),shaftwidth=0.02,headwidth=0.02,color=vec(0,1,0))
arrZ=arrow(pos=vec(0,0,0),axis=vec(0,0,6),shaftwidth=0.04,headwidth=0.02,color=vec(0,0,1))
ring(pos=vec(0,0,0),radius=R,axis=vec(0,0,1),color=vec(1,1,1),thickness=0.02)
ring(pos=vec(0,0,Z2),radius=R,axis=vec(0,0,1),color=vec(1,1,1),thickness=0.02)
[sphere(pos=vec(-0.7+0.2*i,0.0,0),color=vec(0,0.5,1),radius=0.05) for i in range(8)]
arrow(pos=vec(0,R,0),axis=vec(-0.3,0,0),shaftwidth=0.04,color=vec(1,1,0))
bc=vec(1,0.5,0)
for i in range(8):
#scene.pause('click')
xi=-0.7+0.2*i
r=vec(xi,0.0,0)
Bline(R,Z2,Ni,ic,r,br,bc,bc)
NC=20
|
|
|
glowscript:二電流環所建立的磁場(磁瓶子)(PS-BFL-2current-loops.py) | |
磁力與運動-1(空間中的均勻磁場)
|
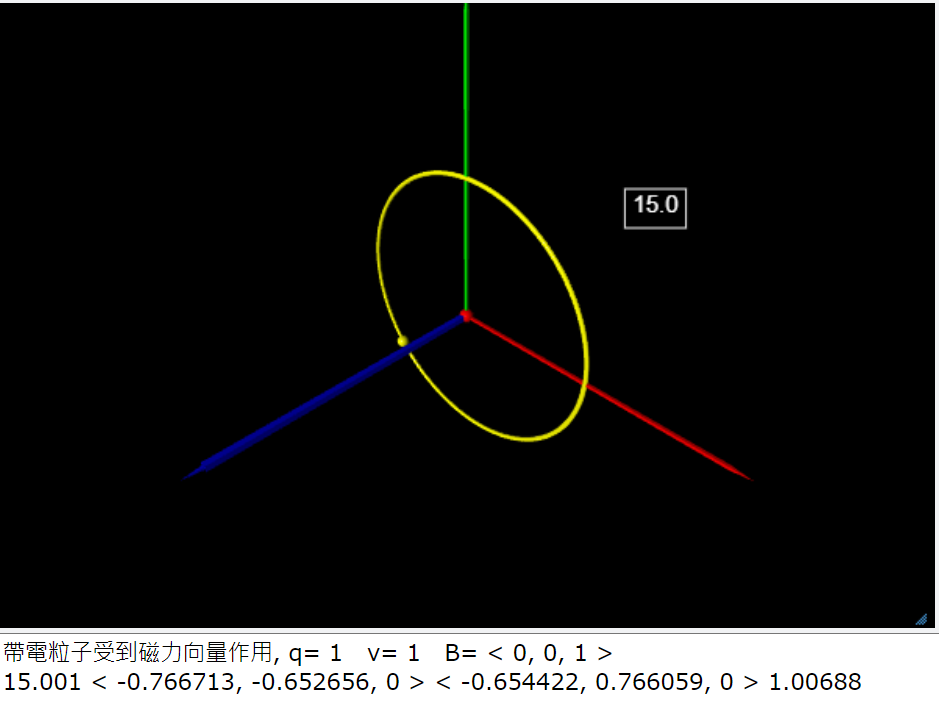
空間中存在一個均勻的磁場,這個磁場是廣泛存在於整個空間當中,因此這個帶電荷的粒子一開始運動就遭受到磁場的作用。磁場的方向是指向+z的方向,具有固定的方向和大小,因此這個帶電粒子在這個磁場中會進行圓週運動。因為粒子的速度和磁場垂直,磁力的方向也會與這兩個方向垂直,因此會形成圓週運動所需的向心力。 circular motion of a charged particle in a uniform magnetic field. THe magnetic force is defined as a cross product: \[ \vec{F}= q \vec{v} \times \vec{B} \] The force is perpendicular to the velocity so it can change the direction of the motion but not its speed. |
 |
GlowScript 3.2 VPython
scene=canvas(width=600, height=400, center=vec(0, 0, 0), forward=vec(-1,-1,-1))
q=1; m=1; r=1.; v=1.
ball0 = sphere(pos=vec(0,0,0), radius = 0.05, make_trail=True, color=color.red)
ball = sphere(pos=vec(r,0,0), radius = 0.05, make_trail=True, color=color.yellow)
arrx=arrow(pos=vec(0,0,0),axis=vec(2,0,0),shaftwidth=0.02,headwidth=0.02,color=vec(1,0,0))
arrY=arrow(pos=vec(0,0,0),axis=vec(0,2,0),shaftwidth=0.02,headwidth=0.02,color=vec(0,1,0))
arrZ=arrow(pos=vec(0,0,0),axis=vec(0,0,2),shaftwidth=0.04,headwidth=0.02,color=vec(0,0,1))
print_options(width=600, height=100)
B=vec(0,0,1)
print('帶電粒子受到磁力向量作用, q=',q,' v=',v,' B=',B)
ball.v=vec(0,-v,0.0)
t=0.; dt = 0.001; NR=int(1./dt)
time='{:04.1f}'.format(t)
T=label(text=time,pos=vector(1.2,1.2,0))
scene.pause('click')
while t < 15:
rate(NR)
time='{:04.1f}'.format(t); T.text=time
ball.a=q*cross(ball.v,B)/m
ball.v += ball.a*dt
ball.pos += ball.v*dt
t=t+dt
print(t,ball.pos,ball.v,mag(ball.pos))
|
|
|
glowscript:磁力與運動-1(PS-MF-motion-1.py) | |
磁力與運動-2(局限空間中的磁場)
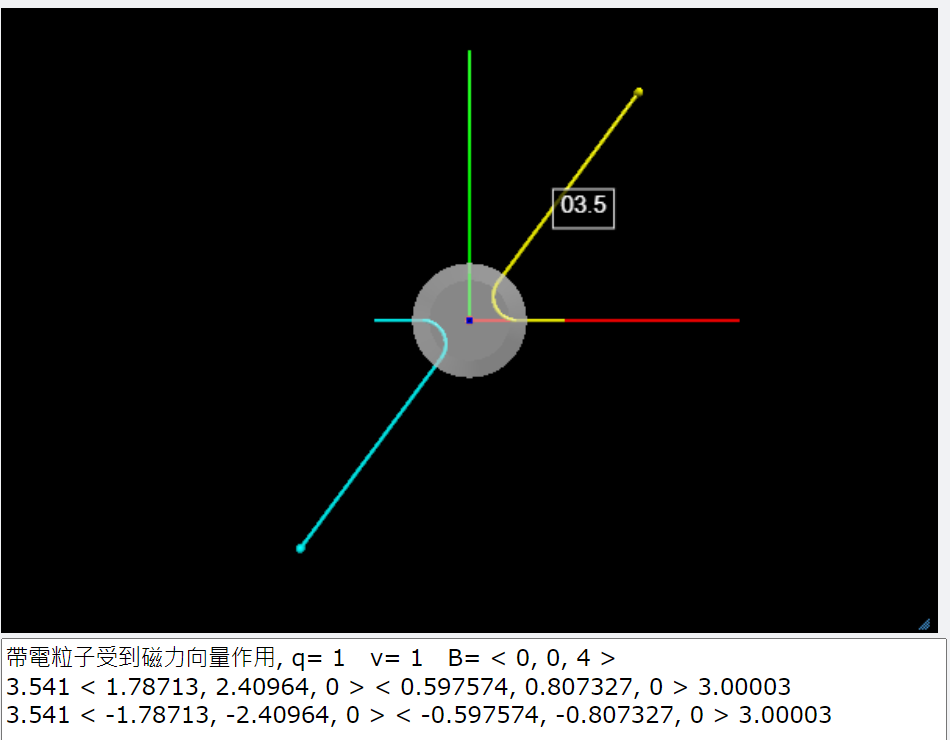
| motion of 2 charged particles due to the uniform magnetic force in a region of a cylinder.在這個問題當中,帶電粒子在圓柱體所在的區域之內才受到一個均勻磁場的作用力,在圓柱體的外圍並沒有磁力的作用。因此帶電粒子起初在圓柱體的外側時,進行等速度直線運動,進入圓柱體的區域候,粒子的速率不會改變但是方向會轉彎。 |
 |
GlowScript 3.2 VPython
scene=canvas(width=600, height=400, center=vec(0, 0, 0), forward=vec(0,0,-1))
q=1; m=1; r=1.; v=1.
ball0 = sphere(pos=vec(0,0,0), radius = 0.05, make_trail=True, color=color.red)
ball1 = sphere(pos=vec(r,0,0), radius = 0.05, make_trail=True, color=color.yellow)
ball2 = sphere(pos=vec(-r,0,0), radius = 0.05, make_trail=True, color=color.cyan)
arrx=arrow(pos=vec(0,0,0),axis=vec(3,0,0),shaftwidth=0.02,headwidth=0.02,color=vec(1,0,0))
arrY=arrow(pos=vec(0,0,0),axis=vec(0,3,0),shaftwidth=0.02,headwidth=0.02,color=vec(0,1,0))
arrZ=arrow(pos=vec(0,0,0),axis=vec(0,0,3),shaftwidth=0.04,headwidth=0.02,color=vec(0,0,1))
cylinder(pos=vec(0,0,-1),axis=vec(0,0,2),radius=0.5,color=vec(1,1,1),opacity=0.5)
print_options(width=600, height=100)
B=vec(0,0,4)
print('帶電粒子受到磁力向量作用, q=',q,' v=',v,' B=',B)
ball1.v=vec(-v,0,0)
ball2.v=vec(v,0,0)
t=0.; dt = 0.001; NR=int(1./dt)
time='{:04.1f}'.format(t)
T=label(text=time,pos=vector(1.2,1.2,0))
#scene.pause('click')
|
|
|
glowscript:磁力與運動-2(PS-MF-motion-2.py) | |
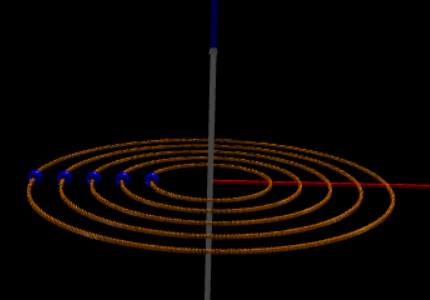 def linecurr(ic,r,La,Lb):
mu0=1.
Nz=40
dz=(Lb-La)/Nz
B=vector(0.,0.,0.)
for i in range(Nz):
rp=vector(0,0,La+dz*i)
dl=vec(0,0,dz)
rrp=r-rp
dB=mu0*ic/4.*pi*cross(dl,rrp)/mag(rrp)**3
B=B+dB
return B
def BF_line(ic,r,La,Lb,a):
maxi=2000
ss=0.01
ri=r
for i in range(maxi):
B=linecurr(ic,r,La,Lb)
curr=1
nr=r+B/mag(B)*ss
arrow(pos=r,axis=nr-r,shaftwidth=0.02,headwidth=0.01,color=a)
r=nr
if(i>100 and mag(r-ri) < 0.08): break
arrx=arrow(pos=vec(0,0,0),axis=vec(2,0,0),shaftwidth=0.02,color=vec(1,0,0))
arrY=arrow(pos=vec(0,0,0),axis=vec(0,2,0),shaftwidth=0.02,color=vec(0,1,0))
arrZ=arrow(pos=vec(0,0,0),axis=vec(0,0,2),shaftwidth=0.02,color=vec(0,0,1))
ic=5
La,Lb=-1.,1.
arrow(pos=vec(0,0,La),axis=vec(0,0,Lb-La),shaftwidth=0.04,headwidth=0.06,color=vec(1,1,1))
[sphere(pos=vec(-1.2+0.2*i,0.0,0),color=vec(0,0.5,1),radius=0.05) for i in range(5)]
br=0.1
bc=vec(1,0.5,0)
for i in range(5):
scene.pause('click')
xi=-1.2+0.2*i
r=vector(xi,0.0,0)
#ball=sphere(pos=r,color=vec(0,0,1),radius=0.05)
BF_line(ic,r,La,Lb,bc)
def linecurr(ic,r,La,Lb):
mu0=1.
Nz=40
dz=(Lb-La)/Nz
B=vector(0.,0.,0.)
for i in range(Nz):
rp=vector(0,0,La+dz*i)
dl=vec(0,0,dz)
rrp=r-rp
dB=mu0*ic/4.*pi*cross(dl,rrp)/mag(rrp)**3
B=B+dB
return B
def BF_line(ic,r,La,Lb,a):
maxi=2000
ss=0.01
ri=r
for i in range(maxi):
B=linecurr(ic,r,La,Lb)
curr=1
nr=r+B/mag(B)*ss
arrow(pos=r,axis=nr-r,shaftwidth=0.02,headwidth=0.01,color=a)
r=nr
if(i>100 and mag(r-ri) < 0.08): break
arrx=arrow(pos=vec(0,0,0),axis=vec(2,0,0),shaftwidth=0.02,color=vec(1,0,0))
arrY=arrow(pos=vec(0,0,0),axis=vec(0,2,0),shaftwidth=0.02,color=vec(0,1,0))
arrZ=arrow(pos=vec(0,0,0),axis=vec(0,0,2),shaftwidth=0.02,color=vec(0,0,1))
ic=5
La,Lb=-1.,1.
arrow(pos=vec(0,0,La),axis=vec(0,0,Lb-La),shaftwidth=0.04,headwidth=0.06,color=vec(1,1,1))
[sphere(pos=vec(-1.2+0.2*i,0.0,0),color=vec(0,0.5,1),radius=0.05) for i in range(5)]
br=0.1
bc=vec(1,0.5,0)
for i in range(5):
scene.pause('click')
xi=-1.2+0.2*i
r=vector(xi,0.0,0)
#ball=sphere(pos=r,color=vec(0,0,1),radius=0.05)
BF_line(ic,r,La,Lb,bc)
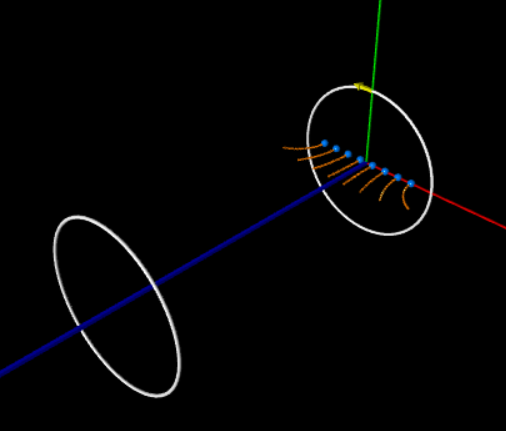
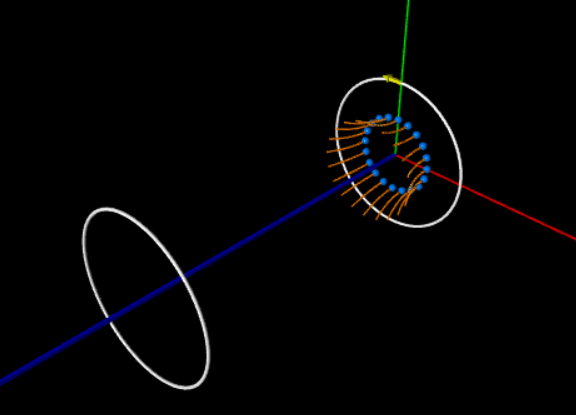 for i in range(NC):
#scene.pause('click')
t=2*pi/NC*i
xi=0.5*cos(t)
yi=0.5*sin(t)
r=vec(xi,yi,0)
Bline(R,Z2,Ni,ic,r,br,bc,bc)
for i in range(NC):
#scene.pause('click')
t=2*pi/NC*i
xi=0.5*cos(t)
yi=0.5*sin(t)
r=vec(xi,yi,0)
Bline(R,Z2,Ni,ic,r,br,bc,bc)
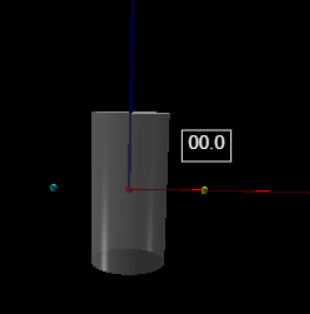 while t < 15:
rate(NR)
if(mag(ball1.pos) > 3): break
if(mag(ball2.pos) > 3): break
time='{:04.1f}'.format(t); T.text=time
rho=sqrt(ball1.pos.x**2+ball1.pos.y**2)
if(rho < 0.5): ball1.a=q*cross(ball1.v,B)/m
else: ball1.a=vec(0,0,0)
ball1.v += ball1.a*dt
ball1.pos += ball1.v*dt
rho=sqrt(ball2.pos.x**2+ball2.pos.y**2)
if(rho < 0.5): ball2.a=q*cross(ball2.v,B)/m
else: ball2.a=vec(0,0,0)
ball2.v += ball2.a*dt
ball2.pos += ball2.v*dt
t=t+dt
print(t,ball1.pos,ball1.v,mag(ball1.pos))
print(t,ball2.pos,ball2.v,mag(ball2.pos))
while t < 15:
rate(NR)
if(mag(ball1.pos) > 3): break
if(mag(ball2.pos) > 3): break
time='{:04.1f}'.format(t); T.text=time
rho=sqrt(ball1.pos.x**2+ball1.pos.y**2)
if(rho < 0.5): ball1.a=q*cross(ball1.v,B)/m
else: ball1.a=vec(0,0,0)
ball1.v += ball1.a*dt
ball1.pos += ball1.v*dt
rho=sqrt(ball2.pos.x**2+ball2.pos.y**2)
if(rho < 0.5): ball2.a=q*cross(ball2.v,B)/m
else: ball2.a=vec(0,0,0)
ball2.v += ball2.a*dt
ball2.pos += ball2.v*dt
t=t+dt
print(t,ball1.pos,ball1.v,mag(ball1.pos))
print(t,ball2.pos,ball2.v,mag(ball2.pos))