立方體高斯面的電通量
立方體高斯面的電通量2
圓柱體高斯面的電通量
|
| |
|
下面我們提供了一個樣本程式可以計算立方體的底面,受到體心位置的電荷的電場向量以及電場通過這個面的電通量。請各位同學把這個程式擴展能夠計算整個立方體的六個面的電通量並且與高斯定律做比較。 | |

|
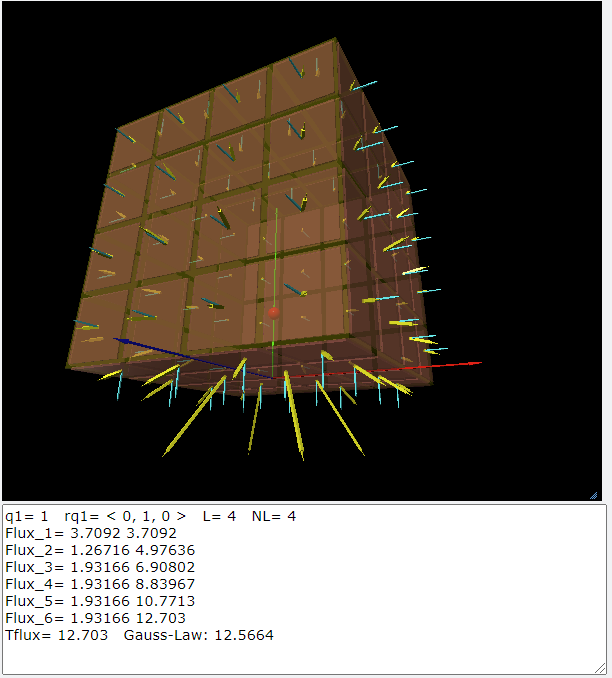
|
GlowScript 3.2 VPython
def EF_point(q,rq,r):
ke=1.; rrq=r-rq
E=ke*q*rrq/mag(rrq)**3
return E
L=4; NL=4; dx=L/NL; dz=L/NL; da=dx*dz
q1=1.; rq1=vec(0,L/4,0.)
scene=canvas(width=600, height=500, center=vec(0.5,L/2,0),forward=vec(-0.5,0.5,-1))
X=arrow(pos=vec(0,0,0),axis=vec(3,0,0),shaftwidth=0.02,headwidth=0.04,color=vec(1,0,0))
Y=arrow(pos=vec(0,0,0),axis=vec(0,3,0),shaftwidth=0.02,headwidth=0.04,color=vec(0,1,0))
Z=arrow(pos=vec(0,0,0),axis=vec(0,0,3),shaftwidth=0.02,headwidth=0.04,color=vec(0,0,1))
Q1=sphere(pos=rq1,radius=0.1,color=vec(1,0,0))
Gauss=box(pos=vec(0,L/2,0),size=vec(L,L,L),color=vec(1,1,0),opacity=0.2)
dx=L/NL; dz=L/NL; dy=L/NL; da=dx*dz;
print('q1=',q1,' rq1=',rq1,' L=',L,' NL=',NL)
Tflux=0
eflux=0; n=vec(0,-1,0)
for i in range(NL):
x=-L/2+dx*(i+0.5)
for j in range(NL):
z=-L/2+dz*(j+0.5)
r=vec(x,0,z)
E=EF_point(q1,rq1,r)
Eda=dot(E,n)*da
eflux+=Eda
box(pos=r,size=vec(dx*0.9,0.03,dz*0.9),color=vec(1,0.5,0.5),opacity=0.3)
arrow(pos=r,axis=E*2,shaftwidth=0.04,headwidth=0.02,color=vec(1,1,0))
arrow(pos=r,axis=n*0.4,shaftwidth=0.02,headwidth=0.02,color=vec(0,1,1))
Tflux+=eflux
print('Flux_1=',eflux,Tflux)
|
|
|
| |

|
youtube:立方體高斯面的電通量2說明影片 |
|
|
|
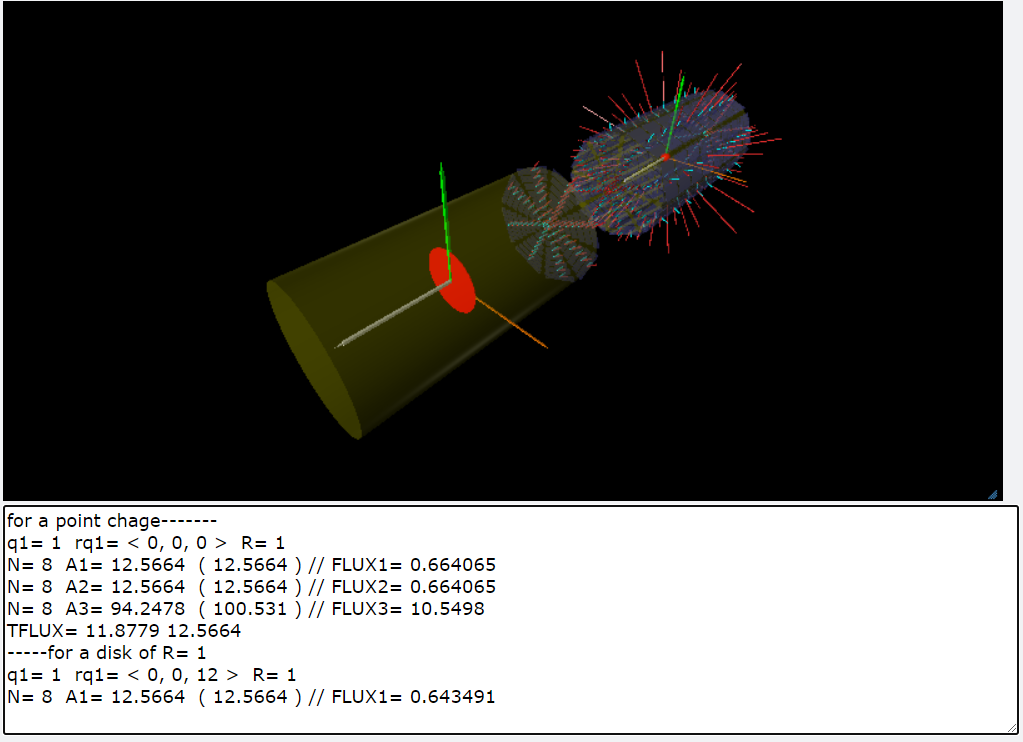
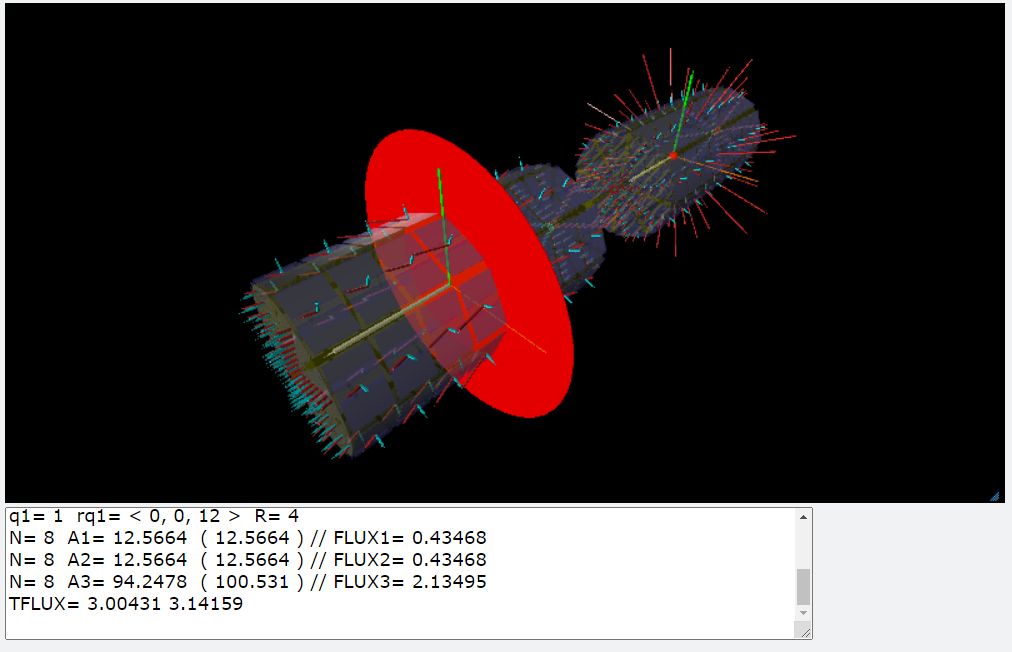
在這個習題當中我們要考慮一個圓柱體的表面所形成的封閉曲面(高斯面)。在這個圓柱體的正中央我們放置了一個點電荷,點電荷的位置設定為座標的原點,圓柱體的軸心為直角坐標系的z軸。我們把圓柱面分成3個部分,圓柱1.上和2.下兩個圓,再加上3.側邊的曲面,共有三個部分。 1. 首先請同學們計算出點電荷所發出的電場通過這3個面的電通量各為多少,並檢查是否與高斯定律所預期的電通量相符合。 2. 第二個部分,我們考慮把點電荷的電量向外擴展成為一個躺在xy-平面的圓盤面。圓盤總電量維持q彈,而圓盤的半徑\(R\)逐漸變大,同學們可以假想這是一個帶電圓盤圓盤的半徑R圓盤上的電荷密度為\(\sigma=\dfrac{q}{4\pi R^2}\),單位面積上的電荷量,我們稱為面電荷密度。將圓盤切割成\(N \times N\)的面積單元,而每一個單元的面積上面電荷(\(\mathrm{d}q=\sigma \mathrm{d}a, \,\, \mathrm{d}a=(\mathrm{d}r) (r \mathrm{d} \theta)\))。計算所有面積單元內的電荷在高斯面上任何一點所建立的電場並且計算該高斯面積單元的電通量,以此類推可以計算出整體帶電圓盤在高斯面各處所形成的電場向量與電通量,透過這些計算同學們又可以再一次驗證高斯定律。並且也請同學們觀察,當圓盤的半徑逐漸變大的時候(但是總電量維持不變),高斯面上電場向量如何變化。 3. 第三個部分與圓盤的情況類似,但是將點電荷沿著中心軸線的方向,上下延伸成為一個均勻的帶電線段。同學們可以根據線段的長度和電荷的總量,計算出線電荷密度\(\lambda=q/L\),單位長度內的電量,稱為線電荷密度。將線段切割成均勻的N等份,再計算每一個線單元內的電荷\(\mathrm{d}q=\lambda \mathrm{d}l=q/N\),對高斯面上電場的貢獻。請畫出類似於第1,2部分的電場向量圖,同時也觀察高斯定律是否在直線的電荷分佈下仍然維持不變。同學們可以觀察圓柱體的表面3部分的電通量,隨著電荷分佈的型態變化,其電通量如何跟著變化。 整體而言,這個作業的目的是希望透過程式設計的過程,加深各位同學對於高斯定律的認識,以及對電場與電荷互動關係的內容,並且能夠建立電磁學的數學基礎:用向量加上一些微分與積分之間的關係,而建立起的一個有用的學問。把電磁學學好了,你的物理跟數學的能力都會提升,如果你又能夠順利地用vpython的語言把這個習題做出來,那麼你的程式語言能力也向上提升。因此老師非常鼓勵同學多花一點精神,把這個習題徹底了解,並且能夠順利完成。有任何困難歡迎跟同學、學長和老師討論 youtube:PS-HW-06-02:圓柱體高斯面的電通量 | |