簡諧運動
解說簡諧運動的影片
簡諧運動的精確解 簡諧運動的差分近似 簡諧運動的模擬中加入彈簧
簡諧運動的方程式如下:
Web VPython 3.2
size = 0.3 #球的半徑
r = 0. #平衡點的位置
k = 10 #彈簧的彈性係數
m = 2 #簡諧震盪物體的質量
w=sqrt(k/m) #簡諧震盪的角頻率
A=3. #簡諧震盪的振福
scene = canvas(width=600, height=400, center=vec(0, 0, 0))
ball = sphere(radius = size, color=color.red)
ball.pos = vector(r+A ,0, 0) #簡諧震盪物體的初始位置
arr=arrow(pos=ball.pos*2, axis=vec(-4*A,0,0), \
shaftwidth=0.02, headwidth=0.06)
arrow(pos=vec(0,-2,0), axis=vec(0,4,0), \
shaftwidth=0.02, headwidth=0.06)
t=0.; dt = 0.01; NR=int(1/dt)
while True:
rate(NR)
#球的位置向量直接以精確解的函數代進去
|
 |
Web VPython 3.2
size = 0.3 #球的半徑
r = 0. #平衡點的位置
k = 10 #彈簧的彈性係數
m = 2 #簡諧震盪物體的質量
w=sqrt(k/m) #簡諧震盪的角頻率
A=3. #簡諧震盪的振福
scene = canvas(width=600, height=400, center=vec(0, 0, 0))
ball = sphere(radius = size, color=color.red)
ball.pos = vector(r+A ,0, 0) #簡諧震盪物體的初始位置
ball.v=vec(0,0,0)
arr=arrow(pos=ball.pos*2, axis=vec(-4*A,0,0), shaftwidth=0.02, headwidth=0.06)
arrow(pos=vec(0,-2,0), axis=vec(0,4,0), shaftwidth=0.02, headwidth=0.06)
scene.pause('click')
t=0.; dt = 0.01; NR=int(1/dt)
while True:
rate(NR)
ball.v+=(-k*ball.pos/m)*dt
ball.pos+=ball.v*dt
t=t+dt
|
 |
GlowScript 3.0 VPython R=0.3; r=0.; k=20.; m=2.; A=3 w=sqrt(k/m) scene=canvas(width=600, height=400, center=vec(0, 0, 0)) ball1=sphere(pos=vec(r+A ,0, 0),radius=R, color=color.red) pin=vec(-5,0,0) arr=arrow(pos=ball1.pos*2, axis=vec(-4*A,0,0), \ shaftwidth=0.02, headwidth=0.06) |
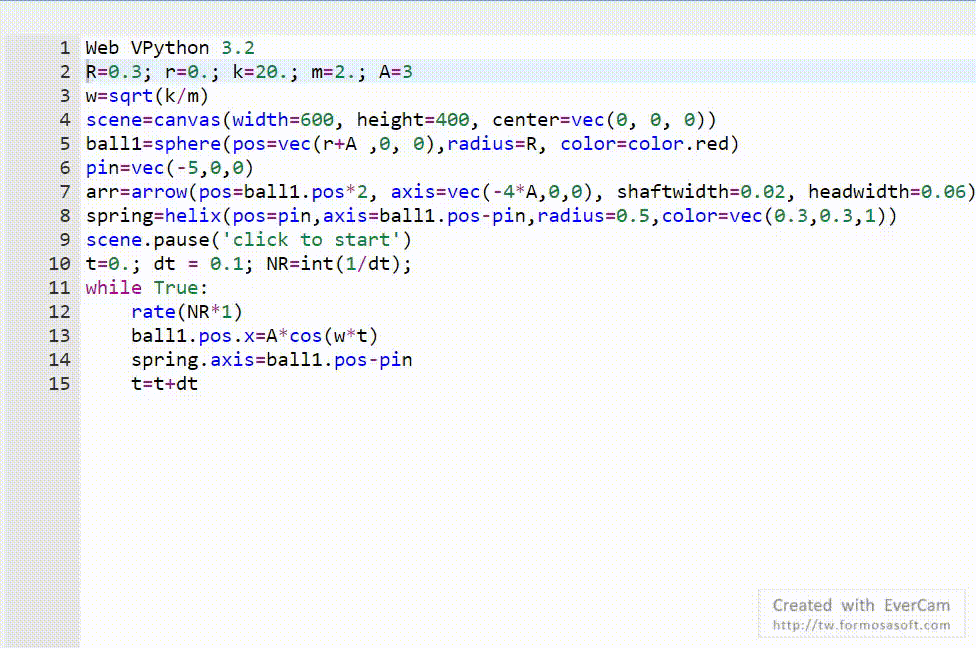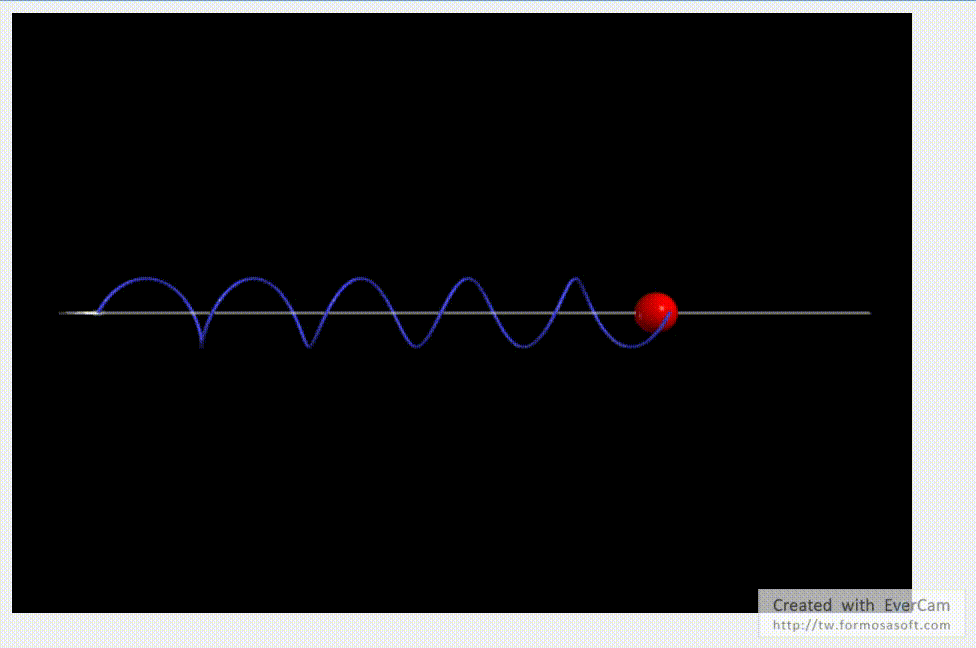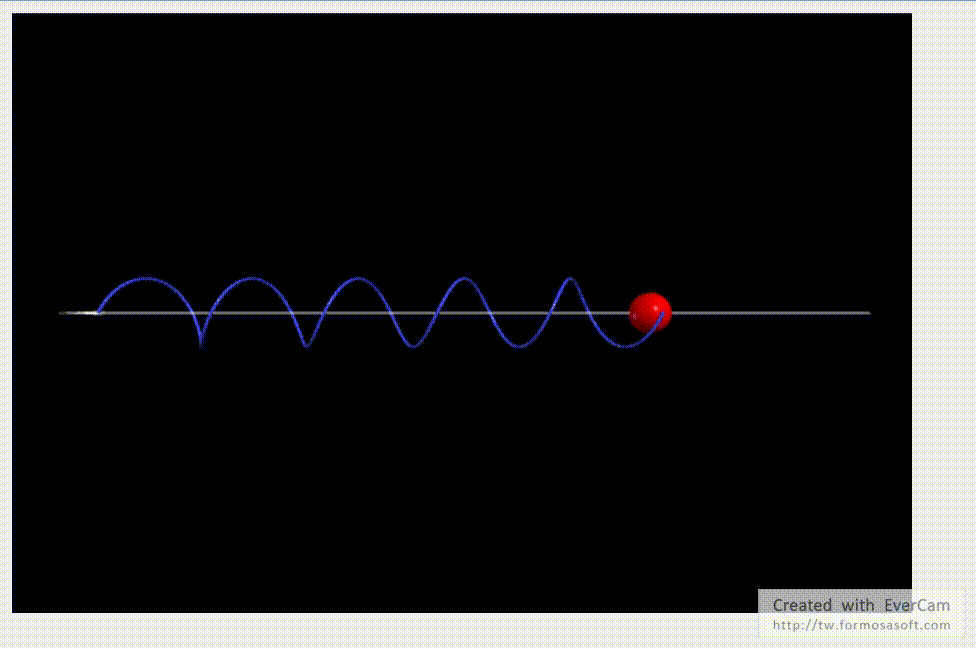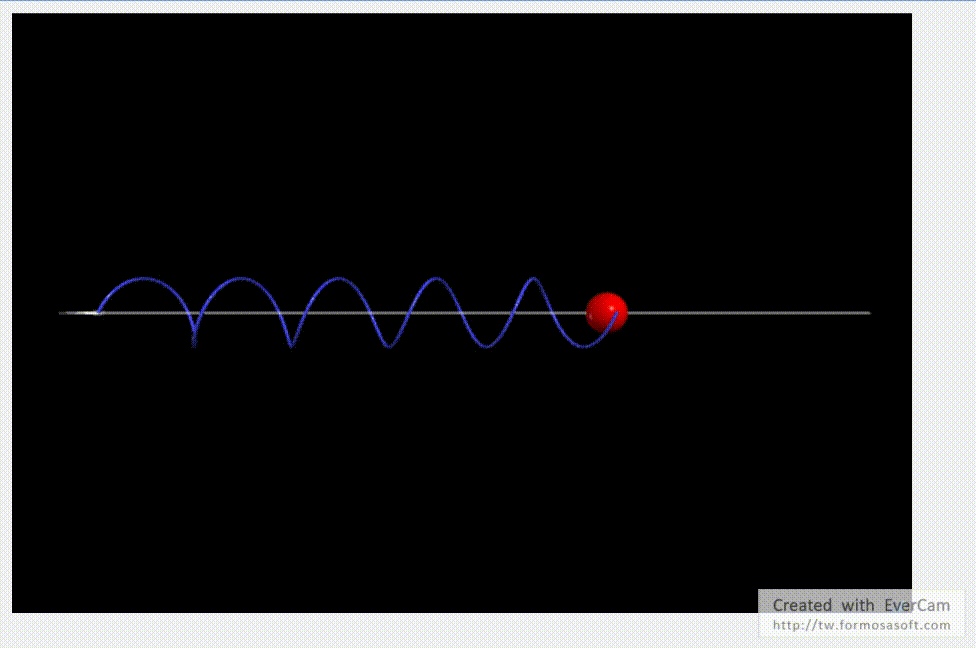 |